|
| [701] Kemény Legény | 2011-12-29 01:30:08 |
 Erről a maradékosztályos témáról eszembe jutott egy viszonylag nehéz feladat (nem saját). Azt hiszem, a fórumon még nem szerepelt:
Legyen p>2 prímszám, és tekintsük a
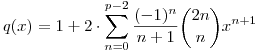
egész együtthatós polinomot. Bizonyítsuk be, hogy q-nak van gyöke modulo p, azaz létezik olyan x egész, hogy q(x) osztható p-vel.
Példa: p=7 esetén a polinom:
q(x)=1+2x-2x2+4x3-10x4+28x5-84x6.
Ennek az értéke pl. x=5 esetén q(5)=-1230789 osztható 7-tel, azaz p=7-re az állítás teljesül.
Továbbá megkönnyítendő az ellenőrzést, elárulom, hogy p=3, 5, 7, 11, 13, 17, 19 esetén az alább x-ek rendre jó választást adnak: x=2, 1, 5, 8, 3, 4, 14.
|
|
| [700] vogel | 2011-12-28 22:36:27 |
 Ha az 1-et tekinti egységnek, akkor 2 inverze 4 mod 7, ha a szorzás a művelet.
|
|
| [699] Kemény Legény | 2011-12-28 22:14:29 |
 Azért az nem kellene elfelejteni, hogy testben lehet osztani 0-tól különböző elemmel, és a 7 szerencsés módon egy prím, ezért a mod 7 maradékosztályok testet alkotnak.
|
| Előzmény: [697] HoA, 2011-12-28 21:31:30 |
|
| [698] Füge | 2011-12-28 21:50:22 |
 Kongruenciát úgy oszthatsz, ha a mod-ot is leosztod a mod és az osztó legnagyobb közös osztójával. Tehát a 2 kongruens 8 (mod 6)-ból következik, hogy 1 kongruens 4 (mod 3).
|
| Előzmény: [697] HoA, 2011-12-28 21:31:30 |
|
| [697] HoA | 2011-12-28 21:31:30 |
 De ezt ugye butaságnak tartjuk? Még egészekre sem igaz ilyesmi. Pl. 2 kongruens 8 ( mod 6 ) -ból nem következik 1 kongruens 4 ( mod 6 )
|
| Előzmény: [695] Hölder, 2011-12-27 00:03:56 |
|
|
|
|
|
|
|
|
| [689] jonas | 2011-12-23 22:03:58 |
 A faktoriálisos kifejezés (5 óránál) az túl nagy szerintem. 9! az legalább százezer, annak a gyöke is legalább száz, ha abból kivonunk 9/9-et, az még mindig legalább száz.
|
| Előzmény: [687] lorantfy, 2011-12-23 13:10:32 |
|
| [688] lorantfy | 2011-12-23 14:12:49 |
 Ha mindet érted, akkor matematikus BSC diploma! :-)
|
 |
|
| [687] lorantfy | 2011-12-23 13:10:32 |
 Hol a hiba? 10 másodperced van, hogy kitaláld! 10, 9, 8...
|
 |
|
|
| [685] patba | 2011-11-29 16:36:48 |
 Értettem a feladatot, de az FBI nem 9 pontos ujjlenyomatot tárol/használ, hanem 12 pontost. Ekkor 1:1,25.1020 az esélye annak, hogy két különböző ember ujjlenyomata megegyezzen, legalábbis Osterburg szerint. Így viszont már hihető, hogy a 200 millió között nincs két egyforma.
|
| Előzmény: [683] Kemény Legény, 2011-11-29 09:37:24 |
|
|
| [683] Kemény Legény | 2011-11-29 09:37:24 |
 Róbert Gida kérdése szerintem arra utal, hogy ha egy N=64milliárd elemű halmazból visszatevéssel kiveszel k=200millió elemet, akkor annak igen kicsi az esélye, hogy ne legyen köztük 2 egyforma.
Képlettel: annak az esélye, hogy mind különböző:
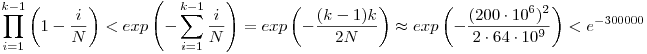
ami egy egészen kis szám, ezért nagyon valószínű, hogy van egyezés a 200millió adat között.
|
| Előzmény: [682] patba, 2011-11-28 22:23:46 |
|
|
| [681] Róbert Gida | 2011-11-28 21:11:29 |
 Egy valódi ujjgyakorlat: Kékfény szerint 9 pontot vizsgáva az ujjon 1 a 64 milliárdhoz annak az esélye, hogy valamely 2 ujjnyom megegyezzen. Elmúlt száz évben nem bukkantak 2 egyforma ujjlenyomatra ((2 különböző embertől)), pedig például az FBI-nál 200 millió ujjlenyomat van.
Mennyire higgyünk a Kékfénynek?
|
|
| [680] kovátsnorbi1994 | 2011-11-12 21:56:45 |
 Helló mindenkinek! Éppen egy hónapja érdeklődtem egy feladatsorral (ill. annak első részével) kapcsolatban, és profi válaszokat is kaptam kérdéseimre - a feladatokat végülis sikerült megoldanom az általatok megadott segítségek felhasználásával (hozzászólásom végén vázlatosan le is írom mire jutottam azokkal), már amennyire emlékszem belőle így néhány hét távlatából... Sajnos azóta elég kevés időm jutott PC elé ülni, így most onnan folytatom, ahol abbahagytam, vagyis a második feladatsorra kérdezek rá: (ezek közül leginkább a II. feladat példáihoz várnék ötleteket, megoldásokat, ott ugyanis elindulni sem tudok, én csak polinomosztással tudnék neki kezdeni, de azt tiltja a feladat...)
* * *
I. Ábrázolja vázlatosan a következő implicit alakban megadott függvényeket:
a.) x+sinx+2x=y+siny+2y b.) sinx=cosy c.) xy=yx 0<x,y
- - -
II. A következő feladatokban a polinom-osztás használatát mellőzzük (ellenőrzésre természetesen használhatjuk) !
a.) Az osztás elvégzése nélkül állapítsa meg a maradékot:
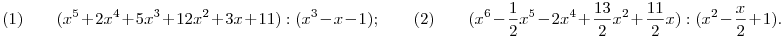
b.) Bontsuk tényezők szorzatára a következő kifejezéseket:
(1) x4+y4–xy(x3+y3)+xy(x2+y2)–8(x+y)+8xy-1 (2) 3xyz+x(y2+z2)+y(z2+x2)+z(x2+y2).
c.) A számláló és nevező átalakításával egyszerűsítsük az alábbi törteket:
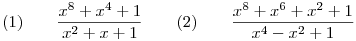
- - -
III. Mutassa meg, hogy
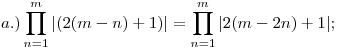

* * *
(Az első feladatsornál az eredményeim tehát:az 1. feladatban a határértékek, ahol léteztek vagyis az a) és c) feladat esetén is, azonosan 1-re adódtak, a 3. feladatban F ' (x)=mF(x)=f(x) ez utóbbi pedig (vagyis a kérdezett primitív függvény meredekségét) éppen a feladatban megadott (derivált)függvény helyettesítési értéke határozta meg az adott helyen, elvégezve a behelyettesítést 0 meredekséget kaptam. A 4. feladatnak (jonas hozzászólását tovább gondolva) minden x-re a=1 és ha b=0 akkor azonosságot kaptam, ami éppen eleget tett a feladat feltételeinek.)
|
| Előzmény: [679] jonas, 2011-10-15 21:03:20 |
|
| [679] jonas | 2011-10-15 21:03:20 |
 Nekem tetszenek ezek a gyakorlófeladatok, és a második adagra is kíváncsi vagyok, de azért jó lenne, ha azt is megosztanád velünk, hogy Te mire jutottál a feladatokkal a tippjeink után. Ha még mindig el vagy akadva valamelyikkel, akkor mondd meg hol.
|
| Előzmény: [676] kovátsnorbi1994, 2011-10-14 20:16:41 |
|
|












