| [135] Csimby | 2004-04-11 22:16:40 |
 42.feladat Bizonyítsuk be, hogy minden húrnégyszög szétvágható n db. húrnégyszögre, ha n 4 poz. egész. 4 poz. egész.
|
|
| [134] Csimby | 2004-04-11 22:10:02 |
 41. feladat Bizonyítsuk be, hogy ha a,b,c egy háromszög oldalai, akkor:
a2(-a+b+c)+b2(a-b+c)+c2(a+b-c) 3abc 3abc
|
|
| [133] Suhanc | 2004-04-10 23:11:06 |
 Kedves László!
Bevallom őszintén, összetörtél bennem egy elképzelést erről feladatról...:)
Nem gondoltam, hogy ilyen elegáns alakban is megkaphatjuk a megoldást, és sok apró lépegetés során hoztam ki egy olyan alakot,amiben már csak a három oldal négyzete szerepel... erre gondoltam, amikor "csavargatásról" írtam...
Hát ez van! ;))
De mindenképp tanulságos volt nekem, köszönöm a megoldást!
|
|
| [132] lorantfy | 2004-03-23 10:47:25 |
 40. feladat megoldása: Hát egyenlő oldalú nem lehet a  mert akkor a nevező 0 lenne. Egyenlő szárú is csak úgy, ha b az egyik szár. Kicsit átalakítva: mert akkor a nevező 0 lenne. Egyenlő szárú is csak úgy, ha b az egyik szár. Kicsit átalakítva:
(a2-c2-b2)(a+c)2=0
Így aztán derékszögű lesz a  , az átfogója: a. , az átfogója: a.
|
| Előzmény: [131] Suhanc, 2004-03-20 15:48:51 |
|
| [131] Suhanc | 2004-03-20 15:48:51 |
 Kedves Veresh!
Köszönöm a megoldást!:) Az esetszétválasztás szerintem nem szükséges, elég azt mondani, hogy "végtelen sok ilyen tulajdonságú szám van, és csak véges sok maradék osztály..." de a Te megoldásod ezt sokkal elegánsabban tálalja.
Egy matematika tesztverseny 10. osztályos feladatsorának feladata volt az alábbi feladat. Nem bonyolult, mégis szép, ahogy csavargatod, hogy kijöjjön a kívánt eredmény...:)
40.Feladat: Egy háromszög a, b, c oldalaira teljesül, hogy  Mit mondhatunk el ekkor a háromszögről? Mit mondhatunk el ekkor a háromszögről?
|
| Előzmény: [130] veresh, 2004-03-15 23:13:30 |
|
| [130] veresh | 2004-03-15 23:13:30 |
 39. feladat megoldása
Legyen n=123456789. Tekintsük a következő sorozatot:
a1=1, a2=11, a3=111, ..., an=1...1
(1) Ha
 i i {1,...,n}: n|ai, {1,...,n}: n|ai,
akkor készen vagyunk.
(2) Ellenkező esetben (legfeljebb) n-1 maradékosztály van. És mivel a sorozat n tagú, ezért a skatulya-elv szerint van a sorozatnak két olyan tagja, amely ugyanabba a maradékosztályba tartozik; formálisan:
 i>j: ai i>j: ai aj(mod n) <==> n|(ai-aj) aj(mod n) <==> n|(ai-aj)
De
ai-aj = 1...10...0 = 1...1.10j
(ahol i-j db. 1-es és j db. 0 számjegy van). És mivel
 j j N: (n,10j) = (32.3607.3803,10j) = 1 N: (n,10j) = (32.3607.3803,10j) = 1
Ezért n|1...1 (i-j db. 1-es). Azaz
 k k N: n.k=1...1 N: n.k=1...1
|
| Előzmény: [129] Suhanc, 2004-03-15 20:17:43 |
|
| [129] Suhanc | 2004-03-15 20:17:43 |
 Kedves László!
Köszöm szépen! Még pár év fórum, és megismerem az egész klaviatúrát...:)
Ez a feladat szerintem nagyon tanulságos, és szép:
39.Feladat. Igazoljuk, hogy 123456789-nek van olyan pozitív egész többszöröse, amelyben csupa 1-es szerepel!
|
| Előzmény: [128] lorantfy, 2004-03-15 12:28:59 |
|
| [128] lorantfy | 2004-03-15 12:28:59 |
 Kedves Suhanc!
Kösz a megoldást! Sokszor jól alkalmazható trükk prímszámos feladatokban, hogy a 3-nál nagyobb prímszámok p=6k 1 esetleg p=12n 1 esetleg p=12n 1 vagy p=12n 1 vagy p=12n 5 alakban írhatók! 5 alakban írhatók!
Az oszhatóság jelet simán be lehet gépelni: AltGr+w kombinációval.
|
| Előzmény: [127] Suhanc, 2004-03-15 08:19:13 |
|
| [127] Suhanc | 2004-03-15 08:19:13 |
 Megoldást írok László 38. feladatára:
Mivel p>3, és prím, ezért nem osztható 3-mal. Négyzetszámok 3-as mardéka 0 vagy 1 lehet, ez esetben tehát csak 1. Tehát p2-1 osztható 3-mal. Mivel p>3vés prím, ezért páratlan. Páratlan négyzetszámok 8-as maradéka 1. Tehát p2-1 osztható nyolccal is. Mivel 8 és 3 relatív prímek, ezért p2-1 osztható 24-gyel.
Lenne egy prózaibb kérdésem: László, az oszthatóságjelet hogyan "gyártottad"? :)
|
| Előzmény: [126] lorantfy, 2004-03-15 00:30:19 |
|
| [126] lorantfy | 2004-03-15 00:30:19 |
 38. feladat: Bbh. ha p>3 prímszám, akkor 24 | p2-1 -nek!
|
|
|
| [124] jenei.attila | 2004-03-11 15:02:18 |
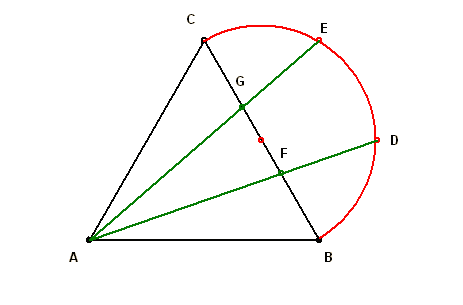
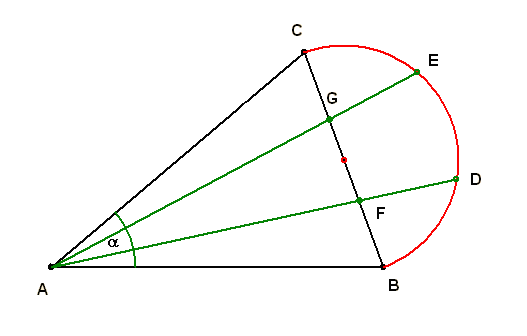
 Még egyszerűbben: BD párhuzamos AC-vel, és fele akkora, ezért BF is fele akkora, mint FC.
|
|
| [123] jenei.attila | 2004-03-11 14:57:35 |
 Vektorokkal megoldva a feladatot, legyen AB=a, AC=b (A-ból B-be mutató vektorról vab szó, csak nem tudok felső nyilat írni). A BC oldal felezőpontja legyen H. Ekkor HD vektor=a/2, és AD vektor=a+b/2. Innen már látszik, hogy az AE és AD szakaszok a BC oldalt harmadolják. AF= 2/3*a+1/3*b.
|
| Előzmény: [122] lorantfy, 2004-03-11 01:29:10 |
|
| [122] lorantfy | 2004-03-11 01:29:10 |
 37. feladat
ABC egyenlő oldalú  BC oldala fölé félkört rajzolunk és ezt D, E pontokkal három egyenlő részre osztjuk. Milyen arányban osztja AD és AE egyenes a BC oldalt ? BC oldala fölé félkört rajzolunk és ezt D, E pontokkal három egyenlő részre osztjuk. Milyen arányban osztja AD és AE egyenes a BC oldalt ?
|
 |
|
| [121] Hajba Károly | 2004-03-02 20:43:48 |
 Kedves Csimby!
Az "átlós kérdés"-nél arra gondoltam, hogy ha egy pont mindkét koordinátája végtelen, elvileg addig már végtelen sok piros vagy kék pontnak kellene lennie, így csorbul a véges feltétel.
A b. feladatrésznél is hasonló lehet a megoldás, csak itt a pontok gyakorlatilag a végtelenségig besűríthetők. Így nem biztos, hogy létezik megoldás.
(Az óvatosságom oka, hogy a végtelennel való műveletekben nem vagyok otthon, nincs kellő gyakorlatom ezzel kapcsolatban.)
HK
|
| Előzmény: [120] Csimby, 2004-03-02 20:23:14 |
|
| [120] Csimby | 2004-03-02 20:23:14 |
 Kedves Onogur!
A megoldásod jó, én is ezt ismertem, bár biztosan(?) van még. A 4 darab átlós irányra vonatkozó kérdésedet nem teljesen értem (a 45°-os egyenesekre gondolsz? és mi a kérdés/feladat?). A b. feladatről mit gondolsz?
|
|
| [119] Hajba Károly | 2004-03-02 13:07:29 |
 Kedves Csimby!
Én a megoldást az alábbi ábra szerint tudom elképzelni. Véges mértékben lehet X-Y irányban tili-tolizni, ill. a színhatár pontjai (mely most kék) akár véletlenszerűen is szinezhetők. (Habár a 4 db átlós irányú végtelenek helyén nem tudom mi a megoldás? :o)
HK
|
 |
| Előzmény: [118] Csimby, 2004-03-01 00:04:18 |
|
| [118] Csimby | 2004-03-01 00:04:18 |
 36.feladat Színezzük meg a koordinátarendszer rácspontjait két színnel, kékkel és pirossal úgy, hogy minden vízszintes egyenesen csak véges sok kék rácspont legyen és minden függőleges egyenesen csak véges sok piros rácspont legyen.
a: Rácspontnak a sík olyan pontjait nevezzük, amelyeknek mindkét koordinátája egész szám.
b: Rácspontnak a sík olyan pontjait nevezzük, amelyeknek mindkét koordinátája racionális szám.
|
|
| [117] Máté2 | 2004-02-24 17:39:17 |
 35. feladat Legyen a H={1, 2, 3, ..., 2000, 2001 } halmaz 77 elemű részhalmazai közül azoknak a száma, amelyekben az elemek összege páros, S-sel egyenlő, és azoknak a száma, amelyekben az elemek összege páratlan, N-nel egyenlő. Melyik nagyobb: S vagy N? És mennyivel?
|
|
| [116] zzz | 2004-02-24 12:31:49 |
 33. megoldása
Tudjuk, hogy f(0)=2. Tegyük fel, hogy f(x) periodikus. Ekkor van olyan x0 0, hogy f(x0)=2 . 0, hogy f(x0)=2 .
Ez azt jelenti, hogy cos (x0)=1 és 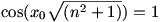 , ,
azaz vannak olyan k1, k2 nem nulla egészek, hogy x0=2k1 és és 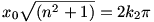 . .
Innen nyerjük, hogy 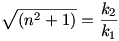 . .
Ez ellentmondás, hisz tudjuk (könnyen igazolható), hogy 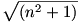 irracionális. irracionális.
|
| Előzmény: [113] Máté2, 2004-02-23 09:23:06 |
|
| [115] Csimby | 2004-02-23 23:09:01 |
 34. feladat megoldása: A négyjegyű számunk 9-cel osztva adjon k maradékot, ekkor a számjegyeinek az összege is k maradékot ad 9-cel osztva a 9-cel való oszthatóság miatt (10,100,1000... 1 maradékot ad 9-cel osztva -> egy szám annyi maradékot ad 9-cel osztva mint amennyit a számjegyeinek az összege). Tehát ha a 4-jegyű számunkból kivonjuk a számjegyeinek az összegét, akkor egy 9-cel osztható számot kapunk. 2+3+4+5+6=20, ez 9-cel osztva 2 maradékot ad, -> a 2-est írtuk hozzá a számhoz.
|
|
| [114] lorantfy | 2004-02-23 21:56:48 |
 Kedves Fórumosok!
Legyen Máté2 [112]-ben leírt feladata a 33. feladat és ezután:
34. feladat: Egy négyjegyű számból elvettem számjegyei összegét, hozzáírtam egy számjegyet, majd sorbarendeztem a számjegyeket és így a 23456 számot kaptam.
Melyik számjegyet írtam hozzá?
|
|
|
| [112] Máté2 | 2004-02-23 09:21:11 |
 Köszönöm a megoldást. Lenne még egy feladatom Bizonyítsuk be, hogy nincs olyan n pozitív egész, amelyre a valós számok halmazán értelmezett f(x)= cosx + cos (x*négyzetgyök alatt: (n2 +1))
|
| Előzmény: [111] lorybetti, 2004-02-22 23:23:42 |
|
| [111] lorybetti | 2004-02-22 23:23:42 |
 Kedves Máté2 és Fórumosok!
Már több feladat is volt mostanában a Kömal pontversenyben a  hozzáírt köreivel kapcsolatban, így ez a feladat a jól megismert összefüggések használatával megoldható: hozzáírt köreivel kapcsolatban, így ez a feladat a jól megismert összefüggések használatával megoldható:
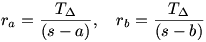
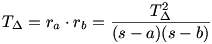
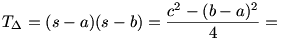
a cos-tételt és a  területképletet alkalmazva: területképletet alkalmazva:
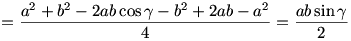
leosztva 2ab-vel:
sin  +cos +cos  =1 =1
mivel  egy egy  szöge, ezért: szöge, ezért:  =90o =90o
(érdemes volt a Tex-el dolgozni, így, hogy már a végeredményt is láttam)
|
| Előzmény: [110] Máté2, 2004-02-22 21:59:03 |
|



 4 poz. egész.
4 poz. egész.  3abc
3abc 

 mert akkor a nevező 0 lenne. Egyenlő szárú is csak úgy, ha b az egyik szár. Kicsit átalakítva:
mert akkor a nevező 0 lenne. Egyenlő szárú is csak úgy, ha b az egyik szár. Kicsit átalakítva: 
 i
i {1,...,n}: n|ai,
{1,...,n}: n|ai, aj(mod n) <==> n|(ai-aj)
aj(mod n) <==> n|(ai-aj) j
j 1 esetleg p=12n
1 esetleg p=12n ?
? 




 0, hogy f(x0)=2 .
0, hogy f(x0)=2 .  és
és 
 +cos
+cos