|
| [426] ágica | 2005-11-09 06:18:00 |
 Én úgy tudom, hogy egy szám lánctört közelítései konvergálnak az adott számhoz, tehát ezt nem kell bizonyítani :) A -1-nek pedig az 1/n sorozat nem a lánctört-közelítéseinek a sorozata :)
|
| Előzmény: [423] Lóczi Lajos, 2005-11-08 23:04:28 |
|
|
| [424] Róbert Gida | 2005-11-09 00:32:00 |
 Ez a 80. feladat elég közismert a diofantikus approximáció elméletben, de azért van elemi megoldása is: Nézzük az 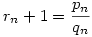 sorozatot, ahol lnko(pn,qn)=1, ekkor a sorozatból pl. p1=3;q1=2 teljesül. Ekkor a rekurzióból: sorozatot, ahol lnko(pn,qn)=1, ekkor a sorozatból pl. p1=3;q1=2 teljesül. Ekkor a rekurzióból:
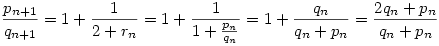
. De mivel lnko(pn,qn)=1 ezért itt a nevező és a számláló relatív prímek, azaz pn+1=2qn+pn és qn+1=qn+pn. Teljes indukcióval könnyen bizonyítható, hogy:
pn2=2*qn2+(-1)n+1
teljesül. Ebből az egyenletből:
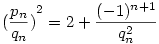
. Mivel a rekurzióból qn szigorúan monoton nő, ezért 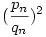 tart 2-höz, de nyilván tart 2-höz, de nyilván 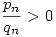 ezért ezért 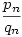 tart tart  -höz, azaz az eredeti sorozat -höz, azaz az eredeti sorozat  -hez. -hez.
|
|
| [423] Lóczi Lajos | 2005-11-08 23:04:28 |
 Körmönfont :) De azt az állítást, miszerint "n növekedésével az n-edik lánctört közelítés egyre jobban megközelíti  -t" hogy lehet bizonyítani? (Ráadásul az, hogy "egyre jobban megközelíti", nem feltétlenül jelenti azt, hogy a limesze is az lenne: pl. -1-et az 1/n sorozat egyre jobban megközelíti...) -t" hogy lehet bizonyítani? (Ráadásul az, hogy "egyre jobban megközelíti", nem feltétlenül jelenti azt, hogy a limesze is az lenne: pl. -1-et az 1/n sorozat egyre jobban megközelíti...)
|
| Előzmény: [422] ágica, 2005-11-08 21:56:41 |
|
| [422] ágica | 2005-11-08 21:56:41 |
 80. megoldás: A sorozat első pár tagját kiszámolva adódhat az a sejtés, hogy a keresett határérték 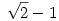 . Ennek bizonyításához határozzuk meg az . Ennek bizonyításához határozzuk meg az 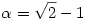 valós szám lánctört közelítéseit. Általánosan, ha valós szám lánctört közelítéseit. Általánosan, ha  irracionális, irracionális,  1= 1= , és n , és n 1 esetén 1 esetén 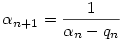 , ahol qn egyenlő , ahol qn egyenlő  n alsó egész részével, akkor n alsó egész részével, akkor  n-edik lánctört közelítése: n-edik lánctört közelítése:
 . .
Ebben az esetben tehát 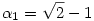 , q1=0, , q1=0, 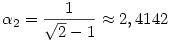 , q2=2. , q2=2.
 3-at kiszámolva azt kapjuk, hogy megegyezik 3-at kiszámolva azt kapjuk, hogy megegyezik  2-vel, tehát q3=q2, így a képzési szabály miatt minden n 2-vel, tehát q3=q2, így a képzési szabály miatt minden n 2-re 2-re  és qn=2. Vagyis és qn=2. Vagyis
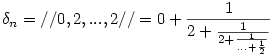 , ,
ami nem más, mint az r sorozat n-1-edik tagja. n növekedésével az n-edik lánctört közelítés egyre jobban megközelíti  -t, ami azt jelenti, hogy -t, ami azt jelenti, hogy
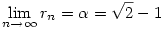 . .
|
| Előzmény: [398] Lóczi Lajos, 2005-10-30 21:17:15 |
|
|
| [420] Róbert Gida | 2005-11-06 12:12:51 |
 81.b feladatra, a sorozatra még egy élesebb egyenlőtlenség is kijött, mint amit a limeszes becslés adna. Eltüntetem először a konstansokat a rekurzióból; szorozzuk a rekurziót 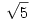 -tel, ekkor: -tel, ekkor: 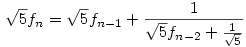 Adjunk mindkét oldalhoz Adjunk mindkét oldalhoz 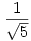 -öt és legyen az új sorozat -öt és legyen az új sorozat 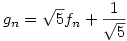 ; ekkor ; ekkor

, ha n>1 és 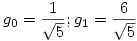
Ez a rekurzió, ha a nevezőben gn-1 lenne, akkor pont az 1975. évi 3. Kürschák példa rekurziója volna! Az ottani ötlettel: emeljük négyzetre a rekurziót, kapjuk:
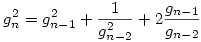
Adjuk össze ezeket az egyenleteket 2-től n-ig, sok tag kiesik, kapjuk:
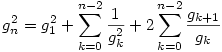 | (1) |
De g1>g0 és a rekurzióból g monoton nő; így a második szumma minden tagja legalább egy:
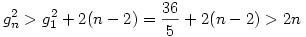
de ez n=0;1-re is teljesül és g tagjai pozitivak, így
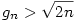
teljesül. Pont ebből az alsó becslésből kapjuk a felső becslést. g sorozatra vonatkozó rekurziót k+1-re felírva: 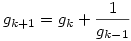 , ezt gk-val osztva: , ezt gk-val osztva: 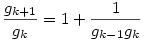 , ha k>0. Így az (1) egyenletből: , ha k>0. Így az (1) egyenletből:
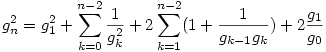
, azaz
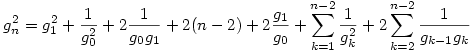
, g monotonitását és g0,g1 értékét használva kapjuk:
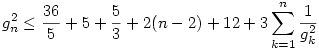
, de 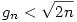 , így , így
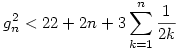
, ismert, hogy 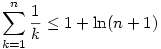 , ha n , ha n 0, így 0, így
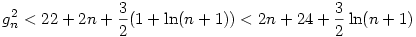
, azaz 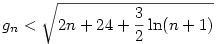 , de ez n=0;1-re is teljesül, így minden n-re igaz. Visszaírva g definicióját és az alsó becslést is használva, kapjuk: , de ez n=0;1-re is teljesül, így minden n-re igaz. Visszaírva g definicióját és az alsó becslést is használva, kapjuk:
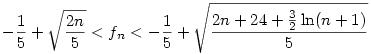
Amiből már látszik a bizonyítandó, sőt ez élesebb becslés is annál.
|
|
| [419] Lóczi Lajos | 2005-11-05 23:00:13 |
 Egy kis heurisztika:
átrendezve a rekurzív egyenletet kapjuk, hogy 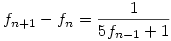 . Fogjuk fel f-et folytonos függvényként. Ekkor a bal oldal körülbelül f '(n), és (némi további elhanyagolással) a következő differenciálegyenletet nyerjük: . Fogjuk fel f-et folytonos függvényként. Ekkor a bal oldal körülbelül f '(n), és (némi további elhanyagolással) a következő differenciálegyenletet nyerjük:
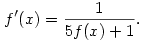
Ezt viszont expliciten meg tudjuk oldani, azt kapjuk, hogy 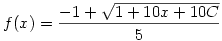 , azaz nagy n-ekre , azaz nagy n-ekre 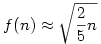 . .
|
| Előzmény: [418] nadorp, 2005-11-05 13:41:09 |
|
|
|
|
|
| [414] lorantfy | 2005-11-01 21:01:10 |
 Kedves Káli gúla!
Ötletes és egyszerű megoldás. Köszönöm! Az enyém túl körülményes.
Felhívom a figyelmedet a 202. feladatra az Érdmatfelben. Egy barátomtól hallottam, aki remélhetőleg hamarosan sakkmester lesz!
|
| Előzmény: [413] Káli gúla, 2005-11-01 20:15:01 |
|
| [413] Káli gúla | 2005-11-01 20:15:01 |
 Kedves László!
Az 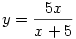 jelöléssel az egyenlet x2+y2=11 alakú. A helyettesítésből (*) xy=5(x-y), ezért jelöléssel az egyenlet x2+y2=11 alakú. A helyettesítésből (*) xy=5(x-y), ezért
x2+y2=(x-y)2+2xy=(x-y)2+10(x-y)=11.
A 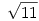 sugarú kör a (*) hiperbolának csak a jobb oldali ágát metszi, ahol y sugarú kör a (*) hiperbolának csak a jobb oldali ágát metszi, ahol y x, így az 1 és a -11 közül csak az x-y=1 gyök jó. Ezt visszaírva (*)-ba az x(x-1)=5 egyenletet kapjuk, aminek a gyökei x, így az 1 és a -11 közül csak az x-y=1 gyök jó. Ezt visszaírva (*)-ba az x(x-1)=5 egyenletet kapjuk, aminek a gyökei 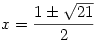 . .
|
| Előzmény: [409] lorantfy, 2005-10-31 13:56:12 |
|
|
| [411] Lóczi Lajos | 2005-10-31 17:47:59 |
 Amit írtál az annyit mond: ha feltesszük, hogy a határérték létezik, akkor az értéke csak 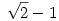 lehet. (Tehát a limesz létét is meg kellene mutatni, de nem muszáj a definíció alapján, ahogyan írtad, egyszerűbb hivatkozni olyan állításokra, mint pl. "ha egy sorozat monoton és korlátos, akkor konvergens" -- ilyesmit kell keresni pl.) lehet. (Tehát a limesz létét is meg kellene mutatni, de nem muszáj a definíció alapján, ahogyan írtad, egyszerűbb hivatkozni olyan állításokra, mint pl. "ha egy sorozat monoton és korlátos, akkor konvergens" -- ilyesmit kell keresni pl.)
|
| Előzmény: [406] Suhanc, 2005-10-31 10:30:45 |
|
|
| [409] lorantfy | 2005-10-31 13:56:12 |
 Kedves Attila!
Kösz a szép megoldást! Beírom az én megoldásomat is.
76. megoldása helyettesítéssel:

 itt legyen itt legyen 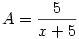 ebből ebből 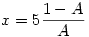 ezt visszaírva az eredeti egyenletbe: ezt visszaírva az eredeti egyenletbe:
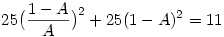
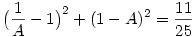
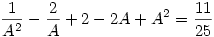

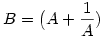
25B2-50B-11=0
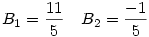
Az első gyök ad valós megoldást A-ra:
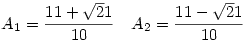
Ezt visszahelyettesítve:

|
| Előzmény: [407] jenei.attila, 2005-10-31 11:58:40 |
|
|
| [407] jenei.attila | 2005-10-31 11:58:40 |
 Végezzük el az y:=-x és
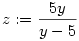
helyettesítést. Ezzel az eredeti egyenlet
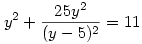
, illetve
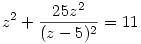
alakú lesz. Vagyis, ha y gyöke az egyenletnek, akkor z is az. De
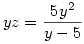
és
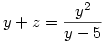
. Ezért a másodfokú egyenlet gyökeinek és együtthatóinak összefüggése szerint y és z egy x2+px-5p=0 alakú egyenelet gyökei, míg az eredeti egyenletből kapott negyedfokú egyenlet 3. és 4. gyöke szintén a x2+qx-5q=0 alakú egyenlet gyökei. Elvégezve a két másodfokú egyenlet összeszorzását és az együtthatók összehasonlítását p=1, q=-11 -et kapunk, amiből az eredeti gyökök könnyen megkaphatók.
|
| Előzmény: [382] lorantfy, 2005-10-29 11:54:41 |
|
| [406] Suhanc | 2005-10-31 10:30:45 |
 Próba-szerencse:
Legyen 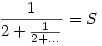 ! !
Ekkor nyilván 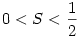 Tehát ezen intervallumon keressük S értékét! Tehát ezen intervallumon keressük S értékét!
Fenti egyenletünk reciprokát véve:

Azaz: 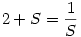
Amiből: S2+2S-1=0
Itt S értékére két lehetőség van, ebből fenti kikötéseinket 1teljesíti: 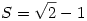
Ez elfogadható S keresés? Avagy szükséges, hogy minden  -ra mutassuk an-t. amire -ra mutassuk an-t. amire 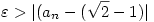 ? ?
|
| Előzmény: [398] Lóczi Lajos, 2005-10-30 21:17:15 |
|
| [405] Edgar | 2005-10-31 07:39:29 |
 jajajj, feladatom törvényen kívül került, mert nem adtam néki számot :-( Legyen:
83. feladat: Oldd meg a természetes számok körében:
x5-y2=4
|
| Előzmény: [393] Edgar, 2005-10-30 19:32:45 |
|
| [404] Róbert Gida | 2005-10-30 23:32:26 |
 A probléma nekem is megtetszett: valóban a Maple 9.5 sem tudja egyszerűsíteni a simplify paranccsal a formulát, ezután megpróbáltam a Mathematica 5.1-gyel, hogy mit tud: az egyszerübb Simplify itt sem egyszerűsít, de a bonyolultabb FullSimplify paranccsal 0.75 másodperc alatt megmondja, hogy az érték 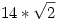 . Csodálatos, hogy már ilyen computeralgebra rendszer is van. . Csodálatos, hogy már ilyen computeralgebra rendszer is van.
|
| Előzmény: [392] Edgar, 2005-10-30 19:21:55 |
|
|





 -t" hogy lehet bizonyítani? (Ráadásul az, hogy "egyre jobban megközelíti", nem feltétlenül jelenti azt, hogy a limesze is az lenne: pl. -1-et az 1/n sorozat egyre jobban megközelíti...)
-t" hogy lehet bizonyítani? (Ráadásul az, hogy "egyre jobban megközelíti", nem feltétlenül jelenti azt, hogy a limesze is az lenne: pl. -1-et az 1/n sorozat egyre jobban megközelíti...) 1 esetén
1 esetén 

 x, így az 1 és a -11 közül csak az x-y=1 gyök jó. Ezt visszaírva (*)-ba az x(x-1)=5 egyenletet kapjuk, aminek a gyökei
x, így az 1 és a -11 közül csak az x-y=1 gyök jó. Ezt visszaírva (*)-ba az x(x-1)=5 egyenletet kapjuk, aminek a gyökei 
 -ra mutassuk an-t. amire
-ra mutassuk an-t. amire 