| [536] sakkmath | 2008-04-01 11:42:22 |
 Kedves Mumin és Suhanc!
A kérdés ismert a sakk-legek irodalmában. A pontos választ is megadták már a matematikus sakkozók (vagy sakkozó matematikusok). Szerintük egy sakkjátszma legfeljebb 5949 lépés hosszú lehet, és ezt a lépésszámot el is lehet érni. Aki nem hiszi, játsszon utána! :-)
Néhány, a sakkrekordokkal foglakozó, érdekes link itt, ott és mindenütt (ha van időnk és kedvünk egyéb webcímeken is keresni, kutakodni...)
|
| Előzmény: [533] Mumin, 2008-03-31 02:48:54 |
|
| [535] Mumin | 2008-04-01 09:10:30 |
 Igen, az világos, hogy nem javítható. De vajon elérhető-e ez? Ugye még egy szabály korlátoz: ha harmadszor is megjelenik ugyanaz az állás, akkor döntetlennel végződik a játszma. Tehát az ütések-gyaloglépések közt úgy kell lépkedni, hogy mindenképp különböző állások legyenek. Ez változtat a helyzeten?
|
| Előzmény: [534] Suhanc, 2008-03-31 16:06:05 |
|
| [534] Suhanc | 2008-03-31 16:06:05 |
 Kedves Mumin!
Nem látok teljesen precíz megoldást, de hát valahol elkezdem...
Amennyire tudom, a játék során tetszőleges egymást követő 50 lépésben gyaloglépésnek, vagy ütésnek kell történnie (ellenkező esetben döntetlen: hozzáértők esetleg világosítsanak fel, hogy ekkor igényelhető csupán a döntetlen, vagy egy játszmalapot vizsgálva a bíró is kinyilváníthatja...)
Ha a fenti megkötések érvényesek, úgy legfeljebb 14 bábút üttethetünk le, és mind a 16 gyalog legfeljebb 7 mezőt léphet. Ennek alapján legfeljebb 126*50= 6300 lépést tehetnek meg.
Kérdés, hogy ennyi megtétele lehetséges-e. Vélhetően nem, mert az azonos oszlopban álló gyalogok akadályozzák egymást. Vagy gyaloggal ütünk gyalogot (akkor egyszerre ütés és gyaloglépés is történt, -50 lépés), vagy gyaloggal ütünk le másik bábút, ám ez is ugyanezt eredményezi.
Alulról elindulva: Ha a könnyűtiszteket leüttetjük a gyakologokkal, el tudjuk érni, hogy "kettes sorba" álljanak, és ekkor már szabad az út. Itt összesen 8 ütés+gyaloglépés történt egyszerre, tehát buktunk 8*50=400 lépést. Ez egy konstrukció 5900 lépésre. Azt sejtem, hogy nem javítható.
|
| Előzmény: [533] Mumin, 2008-03-31 02:48:54 |
|
| [533] Mumin | 2008-03-31 02:48:54 |
 Milyen hosszú (hány lépés) lehet legfeljebb egy szabályos sakkjátszma?
|
|
|
|
|
|
| [528] nemtommegoldani | 2008-03-03 14:43:38 |
 Kedves lorantfy! A megoldás mostmár tényleg érthető, és nagyon szépen köszönöm! Közben én is megoldottam a kockás feladatot, és nagyon örülök neki,én ugyanígy gondolkodtam. Mégegyszer köszönöm a gyors segítséget!!
|
|
|
|
| [525] HoA | 2008-03-02 11:37:20 |
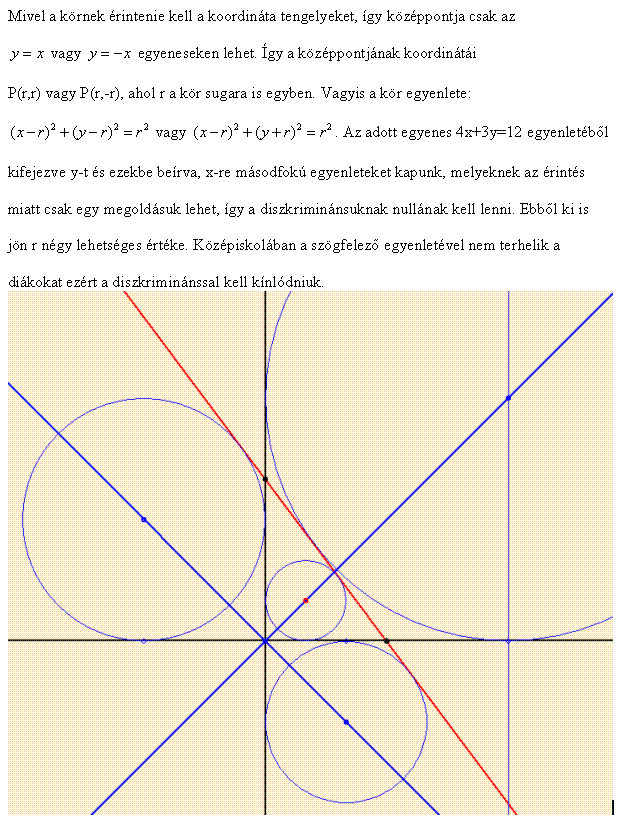
 Gondolj arra, hogy egy háromszög beírt és 3 hozzáírt körét kell megkeresni. Az oldalegyenesek adottak. Egyik a 4x+3y=12 egyenlettel. A másik kettő a két koordinátatengely: y = 0 és x = 0. Rajzold le. A három egyenletből páronként egyenletrendzert képezve a csúcsok (0;0) (3;0) (0;4) . De a csúcsok kiszámítása nélkül is a megadott képlettel két-két egyenespár , például ( x = 0 ; y = 0 ) és ( x = 0 ; 4x+3y=12 ) szögfelezőit felírhatjuk. A +- előjelet figyelembevéve 2-2 egyenes adódik ( legyen f1 és f2 ill. g1 és g2 ) . Ezek metszéspontjai (f1 g1), (f1 g2), (f2 g1) és (f2 g2) adják a négy körközéppontot. Ebben a speciális esetben - a tengelyek egyben oldalegyenesek - a körök sugara megegyezik a középpont koordinátájának abszolút értékével.
|
| Előzmény: [524] nemtommegoldani, 2008-03-01 18:51:41 |
|
| [524] nemtommegoldani | 2008-03-01 18:51:41 |
 Nem egészen értem a feladatmegoldást. Az addig oké, h. tényleg 4 körről lehet szó a megadott feltételek alapján. Az a gondom, h. a megadott egy egyenletből hogyan lépjek tovább. Bocs, de lehet, h. hiányosak a koordinátageo ismereteim. Lehetne kérnem, h. magyaráz(zza)d el nekem a megoldást? Köszönettel.
|
| Előzmény: [519] cauchy, 2008-02-09 13:53:28 |
|
|
|
|
| [520] komalboy | 2008-02-09 14:56:06 |
 Egy kis verseny-feladat... : Egy vállalat a hozzá jelentkezőket egy 25 pontból álló teszttel vizsgálja. A legfrissebben meghiretett állásra 20 fő jelentkezett, kinek a teszteredményei mind különbözőek, semelyik kettő sem azonos teljesen. Mutassuk meg, hogy kiválasztható 19 tesztkérdés úgy, hogy a 20 teszt közül bármely kettő között lesz eltérés ezen 19 kérdés alapján is.
|
|
|
| [518] nemtommegoldani | 2008-02-09 10:45:46 |
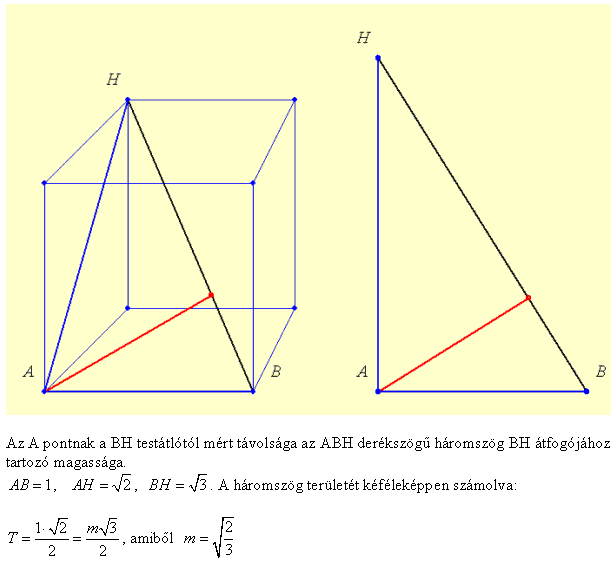
 Feladat1: Mi azon körök egyenlete, amelyek érintik a koordinátatengelyeket, és a 4x+3y=12 egyenest? Feladat2:Adott egy egységkocka, és mondjuk a BH testátló. Mekkora az A csúcsnak a testátlótól való távolsága? (A kocka betűzése:"elölről nézve" alap: ABCD az óramutató járásával ellentétesen,indul A-val a "bal első" csúcstól "teteje": EFGH, szintén az óramutató járásával ellentétesen.) Köszönöm a válaszokat, sokat segítenétek vele.
|
|
|
| [516] komalboy | 2008-01-24 18:13:05 |
 hoztam egy érdekes rekurzív feladatot! már akinek ;) Bizonyítsuk be, h a sorozat tagjai egészek!
|
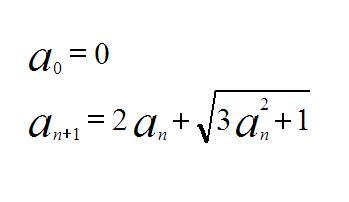 |
|
|
|
|
| [512] Python | 2007-03-21 16:08:38 |
 Ki mondta hogy a Mobius-szalag csak kicsi lehet? Vegyünk egy ~10m kerületű Mobius-szalagot és az elefánt símán átmegy rajta! :)
|
|











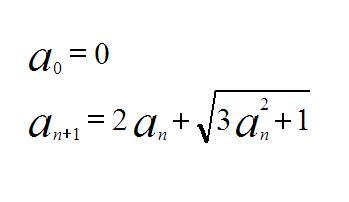


 , a,b
, a,b 0 és
0 és 