Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39]

Szeretnél hozzászólni? Jelentkezz be.

[751] juantheron

2012-06-03 13:09:57

(1) The number of solution of sin (sin (sin x))=cos (cos (cos x))

where x $\in$ [0,2 $\pi$ ]

(2) all ordered pairs (a,b) in 5a²+5b²+5ab=5a+7b

where a,b $\in$ W

[750] Lóczi Lajos	2012-06-02 22:33:25
Akkor (ha addig nem érkezik megoldás) néhány nap múlva adhatsz számunkra tippet az elinduláshoz (pl. egy nagyon speciális esetet konkávitással beláttam, de nem látom, hogy lehet-e az általánosabb esetekben is ezzel érvelni).
Előzmény: [749] sakkmath, 2012-06-02 19:11:24

[749] sakkmath

2012-06-02 19:11:24

Kiegészítések:

1. Maradjunk a feladat eredeti szövegénél:

Az a_i-k pozitív valós számok.

Bizonyítsuk be továbbá, hogy az egyenlőtlenségben egyenlőség akkor és csak akkor áll fenn, ha a₁=a₂=...=a_n .

2. E feladat (is) inkább a "Nehezebb matematikai problémák" fejezetbe való. :( / :)

Előzmény: [748] sakkmath, 2012-06-01 15:21:23

[748] sakkmath

2012-06-01 15:21:23

Egy könnyebb feladat:

Bizonyítsuk be, hogy: ha a₁,a₂,...,a_n nemnegatív valósak, akkor

$\frac{a_1+ \sqrt{a_1a_2}+\dots + \root{n}\of{a_1\dots a_n}}{n}\leqq\root{n}\of{a_1\cdot\frac{a_1+a_2}{2}\dots\frac{a_1+\dots+a_n}{n}}$

[747] Lóczi Lajos	2012-06-01 13:49:17
:-)
Előzmény: [746] HoA, 2012-06-01 11:32:56

[746] HoA	2012-06-01 11:32:56
Akkor lehet, hogy ez sem az a tipikus "ujjgyakorlat" feladat egy középiskolások lapjának fórumán?
Előzmény: [744] Csimby, 2012-05-31 02:43:57

[745] Lóczi Lajos	2012-05-31 16:42:14
Köszönöm. (A Veljan-Korchmáros keresőkifejezésre egyébként egész sok érdekes cikket és általánosítást lehet találni, többek között a Yang S.--Wang J. kínai szerzőpáros cikkeit a 90-es évek közepéről, vagy a V. Volenec--D. Veljan--J. Pecaric hármas cikkét '98-ból.)
Előzmény: [744] Csimby, 2012-05-31 02:43:57

[744] Csimby

2012-05-31 02:43:57

a,b,c oldalú háromszög területe 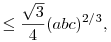$\leq \frac{\sqrt{3}}{4} (abc)^{2/3},$ egyenlőség acsa, ha szabályos a háromszög. Ezt a becslést lehet általánosítani (indukcióval) n-dim szimplexre (ez az n most egy másik n mint az előző hsz-emben - konrétan 1-gyel kisebb): Ha a_ij az A_i és A_j csúcs közti él hossza, akkor a térfogat $\leq 1/n! \sqrt{\frac{n+1}{2^n}}\prod_{1\leq i < j \leq n+1} a_{ij}^{2/(n+1)}.$ Ez D. Veljan sejtése volt, a bizonyítás amit ismerek Korchmáros Gábortól származik, sajnos nem tudom linkelni, de el tudom küldeni ha érdekel (olaszul vagy németül).

Az egyenlőtlenség ebből jön ki (ez az olasz cikkben van), ha a₁,...a_n+1 poz. valósak akkor azt mondod legyen a_ij²=a_i+a_j.

De itt még kell, hogy van ilyen oldalhosszakkal szimplex. Ezt úgy lehet csinálni hogy $\sqrt{a_i}$ -ket felmérünk az n+1-dim tér tengelyeire és akkor ez az n+1 pont jó lesz szimplexnek.

Előzmény: [743] Lóczi Lajos, 2012-05-28 16:46:29

[743] Lóczi Lajos	2012-05-28 16:46:29
Van az egyenlőtlenség megoldására valakinek tippje? (Egyelőre csak n=3-ra van bizonyításom, de abból nem tudok továbblépni nagyobb n-ekre. Valamint tudom, hogy az állítás igaz n=4-re.)
Előzmény: [735] Csimby, 2012-05-22 20:27:55

[742] sakkmath

2012-05-27 12:37:42

I was wrong, sorry.

WolframAlpha computational knowledge engine

Előzmény: [741] Róbert Gida, 2012-05-26 22:10:59

[741] Róbert Gida

2012-05-26 22:10:59

My guess is ...289

9⁹ $\equiv$ 9mod 160

9^9⁹=9^160k+9 $\equiv$ 9⁹ $\equiv$ 89mod 400

$9^{9^{9^9}}=9^{400m+89}\equiv 9^{89}\equiv 289 \mod 1000$

Előzmény: [740] sakkmath, 2012-05-26 15:34:04

[740] sakkmath	2012-05-26 15:34:04
...689
Előzmény: [739] juantheron, 2012-05-25 14:44:28

[739] juantheron

2012-05-25 14:44:28

Thanks sakkmath

Two tasks

(1) last 3 digits of $9^{9^{9^{9}}}$

[738] Róbert Gida	2012-05-22 20:46:03
Úgy már igaz lehet. (n=3-ra jónéhány esetet géppel megnéztem.)
Előzmény: [737] Csimby, 2012-05-22 20:39:10

[737] Csimby	2012-05-22 20:39:10
és ha n>2?
Előzmény: [736] Róbert Gida, 2012-05-22 20:36:16

[736] Róbert Gida	2012-05-22 20:36:16
Legyen n=2;a₁=1;a₂=2, ekkor a két oldal egyenlő, de az a_i-k nem egyenlőek.
Előzmény: [735] Csimby, 2012-05-22 20:27:55

[735] Csimby

2012-05-22 20:27:55

Utolsó próbálkozás: Legyen n $\geq$ 2, a_i-k mint előbb, ekkor:

$\sum_{i=1}^n \frac{a_1a_2\dots a_n}{na_i}\leq \left(\prod_{1\leq i < j \leq n}\frac{a_i+a_j}{2}\right)^{2/n},$

egyenlőség acsa ha a_i-k egyenlőek.

Előzmény: [733] Csimby, 2012-05-22 18:43:47

[734] Róbert Gida	2012-05-22 19:40:14
Ez pedig n=3;a₁=a₂=a₃=2-re nem teljesül.
Előzmény: [733] Csimby, 2012-05-22 18:43:47

[733] Csimby

2012-05-22 18:43:47

Na szóval, legyenek a₁,a₂...,a_n poz. valósak, továbbá n $\geq$ 3 Biz.be:

$\sum_{i=1}^n \frac{a_1a_2\dots a_n}{na_i}\leq \left( \prod_{1\leq i < j \leq n} \frac{a_i+a_j}{2}\right)^{2/(n^2-n)},$

egyenlőség pontosan akkor ha a₁=...=a_n.

Előzmény: [730] Csimby, 2012-05-22 18:12:38

[732] Csimby	2012-05-22 18:33:21
Bocs, a bal oldalt szumma van!!
Előzmény: [731] Róbert Gida, 2012-05-22 18:23:32

[731] Róbert Gida	2012-05-22 18:23:32
n=2;a₁=a₂=8-re nem teljesül az egyenlőtlenség.
Előzmény: [730] Csimby, 2012-05-22 18:12:38

[730] Csimby

2012-05-22 18:12:38

Legyenek a₁,a₂,...,a_n pozitív valós számok. Biz. be:

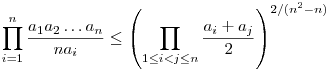
$\prod_{i=1}^n \frac{a_1a_2\dots a_n}{na_i}\leq \left(\prod_{1\leq i < j \leq n} \frac{a_i+a_j}{2}\right)^{2/(n^2-n)}$

Egyenlőség pontosan akkor ha a₁=a₂=...=a_n.

[729] sakkmath

2012-05-19 16:10:25

Az utoljára felvetett kérdésben csak idáig jutottam:

cot (1°).cot (2°).cot (3°).....cot (43°).cot (44°)=tan (46°).tan (47°).tan (48°).....tan (87°).tan (89°)

Ha valaki megkapta volna a szorzat számértékét, kérem, ne tartsa titokban :-)

Előzmény: [727] juantheron, 2012-05-18 17:02:03

[728] sakkmath	2012-05-19 00:25:39
This nostalgia for me: About 30 years ago, I proposed to publish these two problems. (Not published them ...)

Előzmény: [724] sakkmath, 2012-05-18 15:35:51

[727] juantheron

2012-05-18 17:02:03

Thanks Sakkmath i have got my solution after seeing your Answer

bcz I have solve a simillar Problem Yesterday where I have calculate value of sin (1⁰).sin (2⁰).sin (3⁰)......sin (89⁰)

Now I have another doubt in my min

can we calculate the value of

cot (1⁰).cot (2⁰).cot (3⁰)........cot (44⁰)=

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39]

Már regisztráltál?
Új vendég vagy?