|
|
|
| [117] rizs | 2005-01-13 13:53:45 |
 22. feladat: 4 eseményes totó (3 lehetséges kimenetel 1, 2, x) esetén hány szelvény kell a biztos 3 találathoz?
|
|
| [116] Gubbubu | 2005-01-13 11:44:05 |
 21. feladat Adott egy véges T test. Legyen f(a)+f(b)=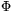 (f(a+b)) és f(a)f(b)= (f(a+b)) és f(a)f(b)=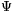 (f(ab)). (f(ab)).
a). Igaz-e, hogy 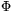 és és 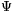 polinomok! (attól tartok, igen, de kíváncsi vagyok, van-e rá valami elemi bizonyítás). Ha ez igaz, hogy néznek ki? polinomok! (attól tartok, igen, de kíváncsi vagyok, van-e rá valami elemi bizonyítás). Ha ez igaz, hogy néznek ki?
b). Mikor bijektívek ezek a leképezések? (mondjuk tudunk-e valami algebrai feltételt adni)
Megjegyzés: felőlem a két görög betűvel jelölt függvény "inverze" is vizsgálható (pontosabban, pl. a  (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb. (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.
|
|
| [115] Atosz | 2005-01-04 18:22:48 |
 Sziasztok!
Először vagyok itt, az érd.mat.fel topikban feltettem [685]-ös hozzászólással két feladatot (137., 138.). Ha valaki tud segítsen! Köszönöm!
|
|
| [114] Bubu | 2004-12-20 15:24:57 |
 Hahó!
Ezt a példán valszám gyakon tűzte ki a tanár n=3-ra, és a megoldásom után azt mondta, hogy Ő még erről nem hallott ilyen formában. n=2-re régen (még mikor én is küldtem) 5 pontos B feladat volt. Sorry,de Texezni nem t'ok.
Feladat: Legyenek A(1), A(2), ..., A(n) tetszőleges események. Metszetük legyen A. Keressük meg a P(A)-P(A(1))*P(A(2))*...*P(A(n)) kifejezés legnagyobb alsó és legkisebb felső korlátját!
Ha valakinek megvan legyen szíves elküldeni nekem e-mailben a megoldását, mert kíváncsi vagyok, hogy egyezik-e az enyémmel. Majd azért igyekszem ide is rendszeresen ellátogatni.
Soxerencsét a megoldáshoz!
Bubu
|
|
| [113] Kós Géza | 2004-11-12 08:29:11 |
 Amennyire látom, 4 pontra mindig van.
Az illesztendő görbének 5 független paramétere van: a koordináta-rendszer origója (2), iránya, a görbe két paramétere (a,b). Az az 5 pont, amit mutattam, inkább olyasmi, mint amikor három pontra akarunk kört illeszteni, de a három pont véletlenül egy egyenesre esik.
|
| Előzmény: [112] Strenner Balázs, 2004-11-11 16:47:57 |
|
|
| [111] Kós Géza | 2004-11-11 11:48:11 |
 Nem nehéz 5 olyan pontot találni, amire nem lehet szinuszgörbét illeszteni:
A(0,0), B(1,0), C(2,0), D(3,0), E(3,1).
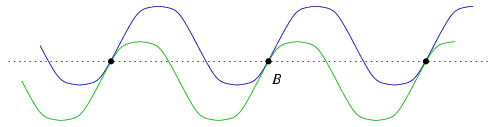
Tételezzük fel, hogy egy szinuszgörbe átmegy az A,B,C pontokon. A görbét középpontosan tükrözve B-re, a tükörkép is átmegy A-n és C-n. Ha B nem a görbe tengelyén van, akkor a görbe és a tükörkép közös pontjai periodikusan helyezkednek el (lásd az ábrát), ezért az AC egyenesnek párhuzamosnak kell lenni a tengellyel. Ugyanez elmondható a B,C,D pontokra is. Ha B és C is a tengelyen van, akkor az ABCD egyenes maga a tengely. Tehát, az ABCD egyenes mindenképpen párhuzamos a tengellyel.
A DE egyenes merőleges a tengelyre, tehát legfeljebb egy pontja lehet a görbén.
|
 |
| Előzmény: [110] Strenner Balázs, 2004-11-10 14:11:56 |
|
| [110] Strenner Balázs | 2004-11-10 14:11:56 |
 A következő probléma valószínűleg elég nehéz, pár napja vetődött fel bennem, és gyanítom, hogy a megoldása meglehetősen bonyolult, feltéve ha van.
Hallottam egy feladatot, miszerint egy szinuszgörbét kell illeszteni 3 pontra. (A szinuszgörbét egy olyan függvény grafikonjaként értelmezem, ahol a koordináta-rendszer a síkban tetszőleges helyzetű, és f(x)=asin (bx) ahol a és b nem 0. Könnyen belátó, hogy van olyan szinuszgörbe, amelyik mindhárom ponton átmegy. Gondoltam, megnézem, mi van 4 pontra. Itt már csak addig jutottam, hogy négyzetre találtam szinuszt, általánosságban azonban nem jutottam semmire. Aztán az is felvetődött, hogy ha 4-re is igaz az állítás, akkor van-e olyan n, hogy n pontot elhelyezve a síkon ne létezzen olyan szinuszgörbe, amelyre mindegyik pont illeszkedik.
Akinek van ötlete, vagy valamit valamit hozzá tud szólni, tegye meg. Köszönöm
|
|
|
|
|
| [106] Gubbubu | 2004-11-02 18:27:00 |
 A "megváltozik" szót úgy értve, hogy az input invariáns sem lehet, hanem kifejezetten más a végén, mint kezdetben... Nem mintha azt várnám, hogy bárki is válaszol erre nekem, de fő a pontosság...
|
| Előzmény: [102] Gubbubu, 2004-10-16 10:32:42 |
|
| [105] Csimby | 2004-10-30 13:42:01 |
 A.350. Adjuk meg az összes pozitív egészt, melyre a 4x2+p polinom a 0,1,...,p-1 helyeken prím értéket vesz fel.
p(x)=4x2+p
p(x)=4x2+p+(4px2-2p-1)-(4px2-2p-1)
p(x)=(p+1)(4x2-1)-(4px2-2p-1)
p(x)=(p+1)(2x-1)(2x+1)+(p+1)-4px2+p
p(x)=(p+1)(2x-1)(2x+1)+(p+1)+p(1-2x)(1+2x)
p csak prím lehet, ellenkező esetben x=0-ra p(x) összetett szám. p=2 nem jó, mert x=1-re p(x)=6, ami összetett. Tehát p páratlan, p+1 páros.
p(x)-et 3 tag összegére bontottuk fel melyek közül az 1. és a 3. osztható 2x+1-gyel. A 2. tag p+1, akkor oszthaó 2x+1-gyel, ha van páratlan osztója, hiszen 2x+1 az x=0,1,...p-1 értékeket veszi fel, vagyis minden páratlan értéket p-ig. Tehát ha p+1-nek van páratlan osztója, akkor van olyan x, hogy p+1 is osztható lesz 2x+1-gyel, tehát p(x) összetett lesz. Az nem jó nekünk amikor p+1-nek csak az 1, a páratlan osztólya illetve az, ha 2x+1=p(x), de ezt kizárhatjuk, hiszen 2x+1<p(x).
Hogyha p+1-nek nincsen 1-en kívül páratlan osztója, akkor p+1=2k, tehát p egy 2k-1 alakú prím, azaz Mersenne-prím. Ismert, hogy ekkor k is prím kell, hogy legyen. Ha k=2, akkor p=3, ez egy jó megoldás. A többi esetben k=4m+1 vagy pedig k=4m-1 alakú. Hogyha k=4m+1, akkor:
p=24m+1-1=2*(22)2m-1 2*(-1)2m-1=1 (mod5) 2*(-1)2m-1=1 (mod5)
Tehát x=1-re p(x) osztható lesz 5-tel, hacsak nem p(x)=5, akkor ez azt jelenti, hogy p(x) összetett (ha p(x)=5, az x=1, helyen, akkor p=1, ami nem prím, ez tehát nem jó).
Maradt az az eset amikor k=4m-1 és ez az ami miatt írtam, mert hogy innen nem tudok tovább menni (lehet, hogy zsákutca?). Hogyha valaki megoldotta másképpen, vagy innen tovább tud menni, az írja be, mert nagyon érdekelne.
Megjegyzés: p=7 is jó megoldás, ahol k=3.
|
|
| [104] Kemény Legény | 2004-10-24 11:20:20 |
 Kedves Bálint!Az ellenpéldád rendkivül meggyőző,és minden további nélkül el is fogadom,azonban ezuton egésziteném ki a megoldást azzal,hogy két kék szomszédos pont között 0 hosszuságu piros sorozatokat definiálunk....
|
| Előzmény: [103] Ureczky Bálint, 2004-10-23 22:34:07 |
|
|
| [102] Gubbubu | 2004-10-16 10:32:42 |
 20. feladat Egy kis algoritmikus kombinatorika:
Van-e "éles" becslés adott n-elemű véges abc feletti k állapotú klasszikus (egyszalagos, egy I/O-fejes, jobbra/balra/helyben lépegető, determinisztikus) Turing-gépek számának felső határára?
Ezek közül hány Turing-gép olyan, ami csinál is valamit, azaz van olyab véges input, amelyre ráeresztve a gépet az megváltozik a számítási eljárás során (nem kell, hogy az eljárás szabályosan érjen véget, az úgy elég nehéz lenne!).
|
|
| [101] Kós Géza | 2004-10-12 12:14:26 |
 Várhatóan péntek körül, amikor már beérkeztek a vidéki dolgozatok, a megoldásokból megint csinálok egy web-oldalt.
Addig is gyűjthetjük a megoldásokat, mert én biztos nem ismerem az összeset. :-)
Az 1. feladatra tudtok szép elemi megoldást?
|
| Előzmény: [95] Csimby, 2004-10-10 01:08:18 |
|
| [100] Kós Géza | 2004-10-11 16:49:44 |
 A feladat annak igazolása, hogy az f(x)ig(x)j alakú polinomok közül kiválasztható néhány, ami lineárisan összefüggő.
Legyen n olyan pozitív egész, ami f és g fokánál is nagyobb. (Azért kell ilyen furcsán fogalmazni, hogy a konstans polinomokból ne lehessen kellemetlenség.)
Tekintsük azokat az fi(x).gj(x) polinomokat, amikre i,j<2n. Ez össesen 4n2 darab polinom. Mindegyik foka legfeljebb 2(2n-1)(n-1)<4n2-1. A kiválasztott polinomok tehát többen vannak, mint az általuk kifeszített tér dimenziója...
|
| Előzmény: [99] Sirpi, 2004-10-11 15:37:09 |
|
| [99] Sirpi | 2004-10-11 15:37:09 |
 19. feladat: Adott két valós együtthatós polinom: f(x) és g(x). Bizonyítsuk be, hogy ezekhez mindig létezik olyan h(y,z) kétváltozós, nem az azonosan nulla polinom, melyre h(f(x),g(x)) 0. 0.
(Saját ötlet, úgy érzem, meg is oldottam, de a megoldásom nem túl szép és vannak benne picit ködös pontok is. Azért tűzöm ki, hátha valaki ad rá egy frappáns megoldást)
|
|
| [98] Kemény Legény | 2004-10-10 20:07:32 |
 A 2. feladatra n=2004+(1002!)2 jon ki,ugyanis n-2004 felbomlik 2004 kulonbozo egesz szorzatara  n-2004 legalabb (-1002)(-1001)..(-1)(1)..(1001)(1002).(Erre van is polinom, -(x-1002)...(x-1)(x+1)...(x+1002)+2004+(1002!)2),ez x=0-ra 2004,x=-1002,...,-1,1,...1002-re pedig eppen n). n-2004 legalabb (-1002)(-1001)..(-1)(1)..(1001)(1002).(Erre van is polinom, -(x-1002)...(x-1)(x+1)...(x+1002)+2004+(1002!)2),ez x=0-ra 2004,x=-1002,...,-1,1,...1002-re pedig eppen n).
|
| Előzmény: [95] Csimby, 2004-10-10 01:08:18 |
|
| [97] Csimby | 2004-10-10 19:50:37 |
 Hú, de szép! Köszi.
|
|
| [96] Kemény Legény | 2004-10-10 19:22:46 |
 Keves Csimby!A 3. feladatnal a piros sorozatok hosszanak valtakozo elojelu osszegenek a harommal valo oszthatosaga nem valtozik egy lepes soran(ellenorizd le,ha nem hiszed).2 kekre ez 0 oszthato 3-mal,mig 2 pirosrara +-2 nem oszthato 3-mal.Igy nem elerheto. A megoldas nem sajat:Molnar Andristol(11.o.)szarmazik.
|
| Előzmény: [95] Csimby, 2004-10-10 01:08:18 |
|



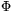 es
es 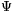 fuggveny. De ha van, akkor termeszetesen polinomok, mert veges test folott minden fuggveny polinom.
fuggveny. De ha van, akkor termeszetesen polinomok, mert veges test folott minden fuggveny polinom. 


 (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.
(f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.



 127 -et akartam írni.
127 -et akartam írni. 2m-1mod(7), ezért 7|4+23n+2-1 és 7|4.49+23n-1 miatt csak m=3n+1 jöhet szóba, azaz k=12n+7. Ekkor viszont
2m-1mod(7), ezért 7|4+23n+2-1 és 7|4.49+23n-1 miatt csak m=3n+1 jöhet szóba, azaz k=12n+7. Ekkor viszont 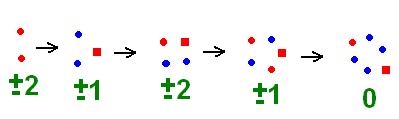

 n-2004 legalabb (-1002)(-1001)..(-1)(1)..(1001)(1002).(Erre van is polinom, -(x-1002)...(x-1)(x+1)...(x+1002)+2004+(1002!)2),ez x=0-ra 2004,x=-1002,...,-1,1,...1002-re pedig eppen n).
n-2004 legalabb (-1002)(-1001)..(-1)(1)..(1001)(1002).(Erre van is polinom, -(x-1002)...(x-1)(x+1)...(x+1002)+2004+(1002!)2),ez x=0-ra 2004,x=-1002,...,-1,1,...1002-re pedig eppen n).