|
| [124] joe | 2005-04-06 19:17:25 |
 23. feladat: Bizonyítsuk be, hogy nem lehet az (euklideszi) síkban véges számú pontot megadni úgy, hogy ha minden egyes pontpár által meghatározott egyenest behúzunk, akkor minden egyes ilyen egyenesre legalább három pont illeszkedik a megadottak közül!
Aki ismeri, ne lőjön agyon érte, hogy beírtam, és ne említsen róla semmi információt! Aki nem ismeri, ÖNÁLLÓAN próbálja megoldani, minden szakirodalom nélkül! Azért tettem ebbe a topicba, mert bár az sem igaz, hogy a megoldás könnyű, az sem igaz, hogy nehéz...
|
|
|
|
|
|
|
|
| [117] rizs | 2005-01-13 13:53:45 |
 22. feladat: 4 eseményes totó (3 lehetséges kimenetel 1, 2, x) esetén hány szelvény kell a biztos 3 találathoz?
|
|
| [116] Gubbubu | 2005-01-13 11:44:05 |
 21. feladat Adott egy véges T test. Legyen f(a)+f(b)=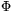 (f(a+b)) és f(a)f(b)= (f(a+b)) és f(a)f(b)=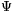 (f(ab)). (f(ab)).
a). Igaz-e, hogy 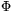 és és  polinomok! (attól tartok, igen, de kíváncsi vagyok, van-e rá valami elemi bizonyítás). Ha ez igaz, hogy néznek ki? polinomok! (attól tartok, igen, de kíváncsi vagyok, van-e rá valami elemi bizonyítás). Ha ez igaz, hogy néznek ki?
b). Mikor bijektívek ezek a leképezések? (mondjuk tudunk-e valami algebrai feltételt adni)
Megjegyzés: felőlem a két görög betűvel jelölt függvény "inverze" is vizsgálható (pontosabban, pl. a  (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb. (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.
|
|
| [115] Atosz | 2005-01-04 18:22:48 |
 Sziasztok!
Először vagyok itt, az érd.mat.fel topikban feltettem [685]-ös hozzászólással két feladatot (137., 138.). Ha valaki tud segítsen! Köszönöm!
|
|
| [114] Bubu | 2004-12-20 15:24:57 |
 Hahó!
Ezt a példán valszám gyakon tűzte ki a tanár n=3-ra, és a megoldásom után azt mondta, hogy Ő még erről nem hallott ilyen formában. n=2-re régen (még mikor én is küldtem) 5 pontos B feladat volt. Sorry,de Texezni nem t'ok.
Feladat: Legyenek A(1), A(2), ..., A(n) tetszőleges események. Metszetük legyen A. Keressük meg a P(A)-P(A(1))*P(A(2))*...*P(A(n)) kifejezés legnagyobb alsó és legkisebb felső korlátját!
Ha valakinek megvan legyen szíves elküldeni nekem e-mailben a megoldását, mert kíváncsi vagyok, hogy egyezik-e az enyémmel. Majd azért igyekszem ide is rendszeresen ellátogatni.
Soxerencsét a megoldáshoz!
Bubu
|
|
| [113] Kós Géza | 2004-11-12 08:29:11 |
 Amennyire látom, 4 pontra mindig van.
Az illesztendő görbének 5 független paramétere van: a koordináta-rendszer origója (2), iránya, a görbe két paramétere (a,b). Az az 5 pont, amit mutattam, inkább olyasmi, mint amikor három pontra akarunk kört illeszteni, de a három pont véletlenül egy egyenesre esik.
|
| Előzmény: [112] Strenner Balázs, 2004-11-11 16:47:57 |
|
|
| [111] Kós Géza | 2004-11-11 11:48:11 |
 Nem nehéz 5 olyan pontot találni, amire nem lehet szinuszgörbét illeszteni:
A(0,0), B(1,0), C(2,0), D(3,0), E(3,1).
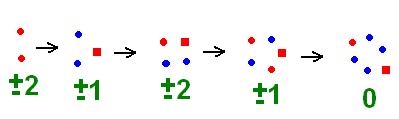
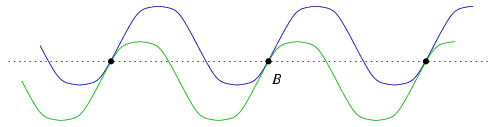
Tételezzük fel, hogy egy szinuszgörbe átmegy az A,B,C pontokon. A görbét középpontosan tükrözve B-re, a tükörkép is átmegy A-n és C-n. Ha B nem a görbe tengelyén van, akkor a görbe és a tükörkép közös pontjai periodikusan helyezkednek el (lásd az ábrát), ezért az AC egyenesnek párhuzamosnak kell lenni a tengellyel. Ugyanez elmondható a B,C,D pontokra is. Ha B és C is a tengelyen van, akkor az ABCD egyenes maga a tengely. Tehát, az ABCD egyenes mindenképpen párhuzamos a tengellyel.
A DE egyenes merőleges a tengelyre, tehát legfeljebb egy pontja lehet a görbén.
|
 |
| Előzmény: [110] Strenner Balázs, 2004-11-10 14:11:56 |
|
| [110] Strenner Balázs | 2004-11-10 14:11:56 |
 A következő probléma valószínűleg elég nehéz, pár napja vetődött fel bennem, és gyanítom, hogy a megoldása meglehetősen bonyolult, feltéve ha van.
Hallottam egy feladatot, miszerint egy szinuszgörbét kell illeszteni 3 pontra. (A szinuszgörbét egy olyan függvény grafikonjaként értelmezem, ahol a koordináta-rendszer a síkban tetszőleges helyzetű, és f(x)=asin (bx) ahol a és b nem 0. Könnyen belátó, hogy van olyan szinuszgörbe, amelyik mindhárom ponton átmegy. Gondoltam, megnézem, mi van 4 pontra. Itt már csak addig jutottam, hogy négyzetre találtam szinuszt, általánosságban azonban nem jutottam semmire. Aztán az is felvetődött, hogy ha 4-re is igaz az állítás, akkor van-e olyan n, hogy n pontot elhelyezve a síkon ne létezzen olyan szinuszgörbe, amelyre mindegyik pont illeszkedik.
Akinek van ötlete, vagy valamit valamit hozzá tud szólni, tegye meg. Köszönöm
|
|
|
|
|
| [106] Gubbubu | 2004-11-02 18:27:00 |
 A "megváltozik" szót úgy értve, hogy az input invariáns sem lehet, hanem kifejezetten más a végén, mint kezdetben... Nem mintha azt várnám, hogy bárki is válaszol erre nekem, de fő a pontosság...
|
| Előzmény: [102] Gubbubu, 2004-10-16 10:32:42 |
|
| [105] Csimby | 2004-10-30 13:42:01 |
 A.350. Adjuk meg az összes pozitív egészt, melyre a 4x2+p polinom a 0,1,...,p-1 helyeken prím értéket vesz fel.
p(x)=4x2+p
p(x)=4x2+p+(4px2-2p-1)-(4px2-2p-1)
p(x)=(p+1)(4x2-1)-(4px2-2p-1)
p(x)=(p+1)(2x-1)(2x+1)+(p+1)-4px2+p
p(x)=(p+1)(2x-1)(2x+1)+(p+1)+p(1-2x)(1+2x)
p csak prím lehet, ellenkező esetben x=0-ra p(x) összetett szám. p=2 nem jó, mert x=1-re p(x)=6, ami összetett. Tehát p páratlan, p+1 páros.
p(x)-et 3 tag összegére bontottuk fel melyek közül az 1. és a 3. osztható 2x+1-gyel. A 2. tag p+1, akkor oszthaó 2x+1-gyel, ha van páratlan osztója, hiszen 2x+1 az x=0,1,...p-1 értékeket veszi fel, vagyis minden páratlan értéket p-ig. Tehát ha p+1-nek van páratlan osztója, akkor van olyan x, hogy p+1 is osztható lesz 2x+1-gyel, tehát p(x) összetett lesz. Az nem jó nekünk amikor p+1-nek csak az 1, a páratlan osztólya illetve az, ha 2x+1=p(x), de ezt kizárhatjuk, hiszen 2x+1<p(x).
Hogyha p+1-nek nincsen 1-en kívül páratlan osztója, akkor p+1=2k, tehát p egy 2k-1 alakú prím, azaz Mersenne-prím. Ismert, hogy ekkor k is prím kell, hogy legyen. Ha k=2, akkor p=3, ez egy jó megoldás. A többi esetben k=4m+1 vagy pedig k=4m-1 alakú. Hogyha k=4m+1, akkor:
p=24m+1-1=2*(22)2m-1 2*(-1)2m-1=1 (mod5) 2*(-1)2m-1=1 (mod5)
Tehát x=1-re p(x) osztható lesz 5-tel, hacsak nem p(x)=5, akkor ez azt jelenti, hogy p(x) összetett (ha p(x)=5, az x=1, helyen, akkor p=1, ami nem prím, ez tehát nem jó).
Maradt az az eset amikor k=4m-1 és ez az ami miatt írtam, mert hogy innen nem tudok tovább menni (lehet, hogy zsákutca?). Hogyha valaki megoldotta másképpen, vagy innen tovább tud menni, az írja be, mert nagyon érdekelne.
Megjegyzés: p=7 is jó megoldás, ahol k=3.
|
|
| [104] Kemény Legény | 2004-10-24 11:20:20 |
 Kedves Bálint!Az ellenpéldád rendkivül meggyőző,és minden további nélkül el is fogadom,azonban ezuton egésziteném ki a megoldást azzal,hogy két kék szomszédos pont között 0 hosszuságu piros sorozatokat definiálunk....
|
| Előzmény: [103] Ureczky Bálint, 2004-10-23 22:34:07 |
|
|
| [102] Gubbubu | 2004-10-16 10:32:42 |
 20. feladat Egy kis algoritmikus kombinatorika:
Van-e "éles" becslés adott n-elemű véges abc feletti k állapotú klasszikus (egyszalagos, egy I/O-fejes, jobbra/balra/helyben lépegető, determinisztikus) Turing-gépek számának felső határára?
Ezek közül hány Turing-gép olyan, ami csinál is valamit, azaz van olyab véges input, amelyre ráeresztve a gépet az megváltozik a számítási eljárás során (nem kell, hogy az eljárás szabályosan érjen véget, az úgy elég nehéz lenne!).
|
|
| [101] Kós Géza | 2004-10-12 12:14:26 |
 Várhatóan péntek körül, amikor már beérkeztek a vidéki dolgozatok, a megoldásokból megint csinálok egy web-oldalt.
Addig is gyűjthetjük a megoldásokat, mert én biztos nem ismerem az összeset. :-)
Az 1. feladatra tudtok szép elemi megoldást?
|
| Előzmény: [95] Csimby, 2004-10-10 01:08:18 |
|





 T? A feladatban ugy tunik, hogy csak egy (T-beli) argumentumok kapnak.
T? A feladatban ugy tunik, hogy csak egy (T-beli) argumentumok kapnak. es
es  fuggveny. De ha van, akkor termeszetesen polinomok, mert veges test folott minden fuggveny polinom.
fuggveny. De ha van, akkor termeszetesen polinomok, mert veges test folott minden fuggveny polinom. 
 (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.
(f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.



 127 -et akartam írni.
127 -et akartam írni. 2m-1mod(7), ezért 7|4+23n+2-1 és 7|4.49+23n-1 miatt csak m=3n+1 jöhet szóba, azaz k=12n+7. Ekkor viszont
2m-1mod(7), ezért 7|4+23n+2-1 és 7|4.49+23n-1 miatt csak m=3n+1 jöhet szóba, azaz k=12n+7. Ekkor viszont