| [139] Sirpi | 2005-04-21 14:28:40 |
 Végül én sem oldottam meg, valaki elmondta órán a megoldást. Továbbra is állítom, hogy szép feladat, és szerintem nehéz. Aki nem ismeri a trükköt, nem könnyen jön rá. Annyit szerintem még nyugodtan elárulhatunk, hogy a Fermat n=4-re való megoldhatatlanságánál a végtelen leszállás módszerére utaltál.
|
| Előzmény: [137] joe, 2005-04-20 20:35:34 |
|
|
| [137] joe | 2005-04-20 20:35:34 |
 Tényleg igaz, amit mesélnek róla? Mármint ami a megoldás kitalálásának időtartamát illeti... Én nem akarom elhinni. Bár én magam nem próbálkoztam vele, hamarabb lőtem le magam előtt könyvből.
|
| Előzmény: [131] Sirpi, 2005-04-19 08:45:03 |
|
| [136] joe | 2005-04-20 20:03:55 |
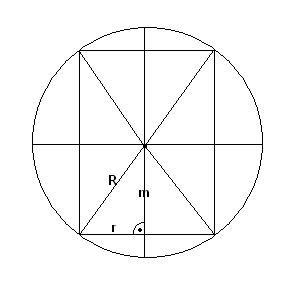
 r*r*m maximumát keressük, ahol r*r + m*m = R*R (m maradjon a "félmagasság"; a legnagyobb félhengerből úgyis könnyen csinálhatunk legnagyobb "egészhengert").
Most állandó R és változó r mellett keressük
(R - m)(R + m)m
kifejezés maximumát. Innen tovább nem akarom lőni, van egy érdekes elemi módszer ilyen esetekre (lényegében algebrai zsonglőrködés): tudjuk, hogyan becsüljünk szorzatot fölülről(?); erre az esetre ezt a módszert egy kicsit kozmetikázni kell, hogy a becslés éles legyen. Hogyan?
|
| Előzmény: [130] lorantfy, 2005-04-18 22:47:44 |
|
| [135] joe | 2005-04-20 19:56:28 |
 Szerintem nem a téglalap max. területét keressük, hanem a henger max. térfogatát keressük...ahogy ez írva vagyon...a forgástestekkel vigyázzunk.
|
| Előzmény: [134] levi, 2005-04-20 18:14:06 |
|
|
| [133] joe | 2005-04-19 19:06:32 |
 Jó, akkor egy kis segítség: a módszer egy kicsit (lényegileg vagy inkább elvileg) hasonlít arra, amivel megmutatják, hogy a nagy Fermat-sejtés igaz a 4-es kitevőre.
|
| Előzmény: [124] joe, 2005-04-06 19:17:25 |
|
|
| [131] Sirpi | 2005-04-19 08:45:03 |
 Én szívesen hozzászólnék, de ismerem a feladatot, úgyhogy inkább csöndben is maradok. Viszont szerintem nagyon jó feladat. Anno, mikor feladták, nem mondták meg, hogy igaz-e az állítás, úgyhogy egy fél füzetet telerajzoltam a különböző konstrukcióimmal :-)
|
| Előzmény: [129] joe, 2005-04-15 18:19:19 |
|
| [130] lorantfy | 2005-04-18 22:47:44 |
 24. feladat: Adjátok meg az R sugarú gömbbe írható max. térfogatú henger méreteit elemi úton!
|
|
|
|
| [127] joe | 2005-04-07 19:40:06 |
 Hát igen, úgy látszik, formában voltam, amikor írtam... Kifelejtettem a "kivéve a minden pont egyetlen egyenesen triviális esetet" mondatot.
|
| Előzmény: [126] Doom, 2005-04-06 20:02:25 |
|
| [126] Doom | 2005-04-06 20:02:25 |
 ööö... nekem úgy tűnik, hogy 3 pont egy egyenesen kielégíti a feladat feltételeit... Vagy csak nem sikerült megértenem a problémát?
|
| Előzmény: [124] joe, 2005-04-06 19:17:25 |
|
|
| [124] joe | 2005-04-06 19:17:25 |
 23. feladat: Bizonyítsuk be, hogy nem lehet az (euklideszi) síkban véges számú pontot megadni úgy, hogy ha minden egyes pontpár által meghatározott egyenest behúzunk, akkor minden egyes ilyen egyenesre legalább három pont illeszkedik a megadottak közül!
Aki ismeri, ne lőjön agyon érte, hogy beírtam, és ne említsen róla semmi információt! Aki nem ismeri, ÖNÁLLÓAN próbálja megoldani, minden szakirodalom nélkül! Azért tettem ebbe a topicba, mert bár az sem igaz, hogy a megoldás könnyű, az sem igaz, hogy nehéz...
|
|
|
|
|
|
|
|
| [117] rizs | 2005-01-13 13:53:45 |
 22. feladat: 4 eseményes totó (3 lehetséges kimenetel 1, 2, x) esetén hány szelvény kell a biztos 3 találathoz?
|
|
| [116] Gubbubu | 2005-01-13 11:44:05 |
 21. feladat Adott egy véges T test. Legyen f(a)+f(b)=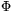 (f(a+b)) és f(a)f(b)= (f(a+b)) és f(a)f(b)=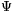 (f(ab)). (f(ab)).
a). Igaz-e, hogy 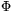 és és 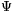 polinomok! (attól tartok, igen, de kíváncsi vagyok, van-e rá valami elemi bizonyítás). Ha ez igaz, hogy néznek ki? polinomok! (attól tartok, igen, de kíváncsi vagyok, van-e rá valami elemi bizonyítás). Ha ez igaz, hogy néznek ki?
b). Mikor bijektívek ezek a leképezések? (mondjuk tudunk-e valami algebrai feltételt adni)
Megjegyzés: felőlem a két görög betűvel jelölt függvény "inverze" is vizsgálható (pontosabban, pl. a  (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb. (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.
|
|
| [115] Atosz | 2005-01-04 18:22:48 |
 Sziasztok!
Először vagyok itt, az érd.mat.fel topikban feltettem [685]-ös hozzászólással két feladatot (137., 138.). Ha valaki tud segítsen! Köszönöm!
|
|





 =
=



 T? A feladatban ugy tunik, hogy csak egy (T-beli) argumentumok kapnak.
T? A feladatban ugy tunik, hogy csak egy (T-beli) argumentumok kapnak.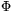 es
es 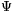 fuggveny. De ha van, akkor termeszetesen polinomok, mert veges test folott minden fuggveny polinom.
fuggveny. De ha van, akkor termeszetesen polinomok, mert veges test folott minden fuggveny polinom. 
 (f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.
(f(a)+f(b))=f(a+b) stb. -t teljesítő függvény), ha úgy könnyebb.