| [191] madár2 | 2005-10-12 15:07:27 |
 az n az fix, mondjuk a számlálóban 4, a nevezőben 5. (de olyan feladat is van, ahol két különböző gyök összege van a számlálóban) a 4. gyök alatt a polinom foka 5, az 5. gyök alatt 6 a foka. (még nem megy a tex, most léptem be először, bocs)
|
|
|
| [189] madár2 | 2005-10-12 13:32:53 |
 Sziasztok! Valaki meg tudná nekem sürgősen mondani, hogy kell megcsinálni, a: végtelen/végtelen tipusú határérték feladatot, ha szerepel/nek banne n.gyökök is, és a gyök alatt álló polinom foka nagyobb, mint az n. (a gyökön) a módszer érdekelne, tudom, hogy nem középiskolás anyag, de fontos lenne. 8tanultam, és elfelejtődött) köszi
|
|
| [188] Lóczi Lajos | 2005-10-12 10:25:21 |
 Persze. Legyen a>1/2. A (konvergencia szempontjából) lényegtelen konstansokat elhagyva elég ezt nézni:
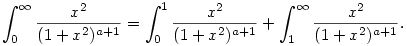
Az első integrandus nyilván korlátos, az integrál tehát véges. A másik integrandus viszont felülről becsülhető
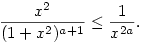
Itt 2a>1, és ismert, hogy ilyenkor 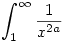 konvergens. konvergens.
|
| Előzmény: [187] rizsesz, 2005-10-11 22:07:36 |
|
| [187] rizsesz | 2005-10-11 22:07:36 |
 minden a>1/2-re konvergens?
|
|
| [186] Lóczi Lajos | 2005-10-11 20:31:32 |
 A végeredmény jónak tűnik, azonban az integrál csak a>1/2 esetén konvergens, különben divergens. (Ha a komplex szám is lehet, akkor a valós része legyen nagyobb 1/2-nél.)
|
| Előzmény: [185] nadorp, 2005-10-11 19:52:32 |
|
| [185] nadorp | 2005-10-11 19:52:32 |
 No comment, ilyen volt a példa, egyszerűbb megoldást nem látok. De lehet, hogy igazad van és legközelebb E-mailben válaszolok a kitűzőnek, ha a példa jóval meghaladja a középiskolai anyagot.
Üdv
|
| Előzmény: [184] hobbymatekos, 2005-10-11 17:02:17 |
|
|
|
| [182] rizsesz | 2005-10-09 23:02:30 |
 Az a baj, hogy a TeX-hez nem értek :( Kezd gyanús lenni, hogy hibás integrál kell ráadásul. Azt elmondhatom esetleg? A lényeg, hogy a feladat a következő volt: Adott egy a paraméterrel rendelkező Pareto-típusú eloszlás: X=1-1/(x+1) ad a, és ezt transzformáljuk Y=gyökX alakba, majd annak kell a várható értéke. Az intervallum o és +végtelen. teX az meg meg lesz tanulva :)
|
|
| [181] Lóczi Lajos | 2005-10-09 16:40:50 |
 (Miért nem TeX-ben írod a képletet? :)
Erre gondolsz?
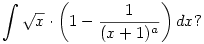
Az általános esetben hipergeometrikus függvény szerepel a képletben, de speciális a-kra (úgy látom, egész vagy egészek fele alakú számokra) elemi függvényekkel is kifejezhető. Pl. a=1 esetén a válasz
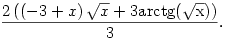
Látogass el a http://integrals.wolfram.com/ címre, ott próbálkozhatsz más a értékekkel is.
|
| Előzmény: [180] rizsesz, 2005-10-09 13:55:45 |
|
| [180] rizsesz | 2005-10-09 13:55:45 |
 Sziasztok! Az alábbi függvényt kellene integrálnom: xad 0,5*(1-1/(x+1)ad a), az ad a hatványozás, ill. "a" tetszőlegesen változtatható paraméter, de úgy nem igazán megy :) és sajna zárt alak kellene. ha bárki tud segíteni, annak előre is köszönöm,
rizsesz
|
|
|
| [178] Stranger | 2005-09-25 16:17:15 |
 Sziasztok nagyon elakadtam, de nem csak én! Ha valaki tudja az vezesse már leegyenlettel, előre is köszi!
Egy villamos sín mellet 4km/h sebességgel haladunk. Minden 12 percben elhagy minket egy villamos, s 4 percenként találkozunk egy szembejövővel . Mekkora a villamosok sebessége, és milyen időközönként követik egymást?
|
|
| [177] hobbymatekos | 2005-09-25 15:07:24 |
 A hengert tartalmazó gömbök közül a minimális térfogatut, a gömbbe irható hengerek közül a maximális térfogatut keressük.A gömb térfogata nagyobb mint a hengeré, térfogataik különbsége pozitiv és minimális. Ha adott egy téglalap, amiről állitjuk, hogy henger középvonalát tartalmazó sikmetszet, akkor az két henger lehet, térfogatuk viszont általában különböző. Ezért elegendő azt mondani, hogy, ha az ilyen kétféle hengerek térfogata egyenlő,tehát a metszet négyzet, akkor a köré irható gömbre nézve max. térfogatú.( Igazolni kell, hogy csak egy max.térfogatú henger irható a gömbbe, másrészt invariáns a forgatásra nézve.) Márpedig a két henger 9o fokos elforgatott.(Egy henger(forgástest) térfogata,(felszine, tömege ha sűrűsége állandó ) a sikmetszetével (sőt már meridiánjával) megadott. Pappus-Guldin tételek.) Másképp: A gömbök és a hengerek között egy m(r,R) fv.feltételezve Vg-Vh min keressük az összes gömbtérfogat és összes hengertérfogat között.(Ez eleminek számit, de nem középiskola. Lagrange multiplikátor módszer). m(r,R) ilyen átviteli fv. szerepü.
|
| Előzmény: [134] levi, 2005-04-20 18:14:06 |
|
|
|
| [174] joe | 2005-07-26 20:00:10 |
 Érdekességek:
Egy derékszögű vonalzóval meg lehet szerkeszteni a másodfokú egyenlet gyökeit;
két derékszögű vonalzóval megoldható a déloszi probléma és a szögharmadolás; szerkeszthető szabályos hét- és kilencszög is.
Ezeket most csak "favágó módjára" kiírtam (Sain Márton: Matematikatörténeti ABC, Szerkesztések címszó), úgyhogy nem tudom, ezek közül mik a nehezebbek. Ha valaki tudja, adja föl feladatnak...
|
|
| [173] joe | 2005-07-26 19:56:24 |
 Én a következő dolgokat találtam: Bármilyen körzővel és vonalzóval elvégezhető szerkesztés elvégezhető:
1) Csak körzővel;
2) Csak körzővel úgy is, hogy adott egy legnagyaobb és egy legkisebb megengedett körzőnyílás;
3) Csak vonalzóval, HA adott egy bármilyen kicsi körív a középpontjával együtt;
4) PÁRHUZAMOS ÉLŰ vonalzóval.
|
| Előzmény: [172] Hajba Károly, 2005-07-25 13:26:01 |
|
| [172] Hajba Károly | 2005-07-25 13:26:01 |
 Üdv!
Viktorhoz hasonlóan már nekem is van "1 körös" megoldásom, de ismerve a feladat forrását ill. egy régebbi, de már kopott emléket, talán meg lehet a feladatot körző használata nélkül is oldani.
Valami dereng, hogy már a görögök is ..., de lényeg, hogy -emlékeim szerint- már jó ideje bizonyított a tény, miszerint, ha egy geometriai szerkesztés megoldható körzővel és vonalzóval, akkor csak az egyikkel is megoldható. Majd megmondjátok, mi igaz ebből.
HK
|
| Előzmény: [165] jonas, 2005-07-04 10:01:56 |
|
| [171] Ali | 2005-07-25 10:24:10 |
 132. feladat.
Bizonyítsuk be, hogy egy téglalap pontosan akkor bontható föl különböző oldalú négyzetekre, ha a téglalap oldalainak aránya racionális szám.
|
|
|
|
| [168] qer | 2005-07-23 21:33:43 |
 131. feladatra: 3 körzőhasználattal megy eddig, még lehet kevesebb?
|
|
| [167] Lóczi Lajos | 2005-07-04 23:02:59 |
 Érdekes a terminológia kérdése, ezen meg is lepődtem.
Nekem a "szimmetriaközéppont" nem feltétlenül jelenti a "középpontos szimmetria" (azaz pontosabban: középpont körüli 180 fokos forgatás) szimmetriapontját. Én azt válaszoltam volna a kérdésre, hogy persze hogy nincs ilyen alakzat, mert forgásszimmetria-középpont mindig van (l. jonas érvelése).
Ki mit gondol a fogalom szempontjából, milyen transzformációk "középpontját" takarhatja a szimmetriaközéppont fogalma?
|
| Előzmény: [159] jonas, 2005-07-02 10:07:10 |
|





