| [222] Lóczi Lajos | 2005-11-28 13:43:22 |
 Szép sejtés (én az "S értékével egy kicsit játszva" lépésben az internetes Inverse Symbolic Calculator-hoz szoktam folyamodni, ami a Sloane-adatbázis kiterjesztése valós számokra.)
Igazoljuk tehát Róbert Gida sejtését, miszerint a feladatbeli összeg értéke 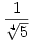 . (A bizonyítás ugyanúgy kell menjen, mint az "ujjgyakorlatok"-beli analóg feladat esetén, amit a Mathematica kiszámolt.) . (A bizonyítás ugyanúgy kell menjen, mint az "ujjgyakorlatok"-beli analóg feladat esetén, amit a Mathematica kiszámolt.)
|
| Előzmény: [221] Róbert Gida, 2005-11-27 16:32:32 |
|
| [221] Róbert Gida | 2005-11-27 16:32:32 |
 Sejtés a 134. feladatra:
n=107-ig összegeztem a tagokat PARI-GP-ben , persze rekurziót használva a tagokra, hogy egy lépésben ne kelljen a faktoriálist kiszámolni, így T=0.6687025753463730983726573923 körülbelül. A maradék tagokra pedig a Stirling formula becslése szerint az n. tag nagyságrendileg: 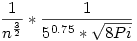 . Így az integrálközelítő összegeket használva egy T-nél jobb becslést is kaphatunk a sorösszegre: . Így az integrálközelítő összegeket használva egy T-nél jobb becslést is kaphatunk a sorösszegre:
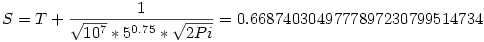
Tehát ennyi jó közelítéssel a sorösszeg. S értékével egy kicsit játszva kiderül, hogy S hihetetlen közel van 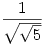 értékéhez, a hiba tőle mindössze 10-12, így valószínűleg ennyi a sorösszeg. értékéhez, a hiba tőle mindössze 10-12, így valószínűleg ennyi a sorösszeg.
|
|
| [220] Róbert Gida | 2005-11-27 15:16:10 |
 Pepin teszt szerint: legyen n>0. Az Fn=22n+1 prím pontosan akkor, ha 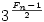 modulo Fn az -1. Így ez a teszt 2n-1 darab négyzetreemelést és redukciót igényel modulo Fn. modulo Fn az -1. Így ez a teszt 2n-1 darab négyzetreemelést és redukciót igényel modulo Fn.
A másik új teszt pedig 2n-2 darab ilyen műveletet igényel, hiszen nekünk itt igazából nem S2n-2 értéke kell, hanem annak modulo Fn vett értéke, így a rekurziót is vehetjük modulo Fn De ott még mindig van 2 kivonása, ami ha binárisan van ábrázolva a szám, akkor átlagosan csak konstans műveletbe kerül.
Így mindkét eljárás lényegében 2n darab négyzetreemelést és redukciót igényel modulo Fn, azaz egyforma gyorsak.
Sőt nagyságrendileg ugyanolyan gyors, mint a Lucas-Lehmer teszt, csak éppen a Mersenne számok jóval sűrűbben vannak, mint a Fermat számok és nem is valószínű, hogy létezne akár még csak egy új prím is a Fermat számok közt, ezért keresnek általában Mersenne prímet.
Még egy dolog a futásidőről: egy sejtés szerint nincs lényegesen gyorsabb prímalgoritmus annál, mint annak a futásideje ami megnézi egy számról log2n négyzetreemeléssel és redukcióval, hogy egy szám egy adott alapra nézve ( erős ) álprím-e. Az előbbiek mind ilyen gyorsak voltak, így nem valószínű, hogy lenne ezeknél gyorsabb algoritmus ezen számokra. Ezért volt számomra nagyon meglepő amikor azt olvastam TRex-től, hogy egy másik algoritmusa szerint ő 25%-kal gyorsabban tudja megcsinálni a Fermat számokra a prímtesztet!, de kiderült, hogy tévedett.
TRex-ről még valamit: hihetetlen egyébként miket meg nem sejt, amik általában ismert tételek a számelméletben:) De ez az eredmény valóban újnak tűnik, én sem láttam sehol hasonlót. Én tőle októberben olvastam ezt a sejtését szintén egy külföldi fórumon: http://mersenneforum.org.
|
| Előzmény: [219] Lóczi Lajos, 2005-11-27 13:32:14 |
|
| [219] Lóczi Lajos | 2005-11-27 13:32:14 |
 És melyik teszt hatékonyabb a Fermat-számokra, a Pepin-féle exponenciális vagy a Reix-féle iteratív? (Úgy értem, melyiket igényel kevesebb számolást?)
T. Reix amúgy egy külföldi fórumon TRex néven tűzte ki ugyanezt a feladatot november elején. Lesz belőle közös cikk? Újnak tűnik az eredmény, nem?
|
| Előzmény: [217] Róbert Gida, 2005-11-27 11:11:30 |
|
| [218] Lóczi Lajos | 2005-11-27 13:26:51 |
 134. feladat. Mennyi a

összeg értéke kifejezve olyan formában, amit még általános iskolában tanultunk?
|
|
| [217] Róbert Gida | 2005-11-27 11:11:30 |
 Valóban nem én vagyok Tony Reix. Ő egyébként egy francia programozó. Váltottunk olyan 6 emailt egymás között a témában, sejtésével kapcsolatban. Nemrégiben adtam rá egy bizonyítást, ami elemi és nem használ tételeket a Lucas sorozatokról. Az ő bizonyítása egyébként hibás, köszönhetően 6. tétel (8.4.7)-nek, mivel ott, hogy mikor van +-1 azt éppenséggel egy Legendre szimbólum adja meg.
Az a legmeglepőbb, hogy a Freud-Gyarmati Számelmélet könyvben a Mersenne számokra vonatkozó kritérium bizonyítását átírva ezt a tételt is meg lehet kapni! Ezt átírva valamivel több mint 2 oldal a bizonyítása néhány könnyen ellenőrizhető számolás kihagyásával. Részletesen olyan 4-5 oldal lenne.
Fermat számokra egyébként a Pepin teszt közismert, ami azért más mint ez a teszt. Éppen szerintem ezért érdekes, hogy a Mersenne és Fermat számokra most már van két hasonló prímteszt, aminek a bizonyítása is hasonló.
Kis segítség a kezdéshez az érdeklödőknek: itt most a ![Q[\sqrt {21}]](keplet.cgi?k=1515E82577882C36) gyűrűben kell dolgozni! Ebben a gyűrűben egyébként igaz a számelmélet alaptétele, de ezt nem kell a bizonyításhoz használni. gyűrűben kell dolgozni! Ebben a gyűrűben egyébként igaz a számelmélet alaptétele, de ezt nem kell a bizonyításhoz használni.
|
| Előzmény: [216] Lóczi Lajos, 2005-11-27 02:39:20 |
|
|
| [215] Róbert Gida | 2005-11-26 22:25:41 |
 133. feladat
Legyen n 1, bizonyítsuk be ekkor, hogy Fn=22n+1 ( azaz az n-edik Fermat szám ) prím akkor és csak akkor, ha az S0=5 és Sk+1=Sk2-2 rekurzióval definiált sorozat esetén az S2n-2 osztható Fn-nel. 1, bizonyítsuk be ekkor, hogy Fn=22n+1 ( azaz az n-edik Fermat szám ) prím akkor és csak akkor, ha az S0=5 és Sk+1=Sk2-2 rekurzióval definiált sorozat esetén az S2n-2 osztható Fn-nel.
|
|
|
|
|
| [211] Wolf | 2005-11-21 11:59:27 |
 Üdv!!!
Szintén Laplace kérdésem van... Adott F(s) törtfv.-nél, ha pólus helyet keresek, pl.: exp(-s*(T/4))=-1 helyen pólus van, akkor ebből hogy jön ki az s*(T/4)=j*k*pi, ahol k=+-1,+-3,+-5,... Fourier-sor meghatározásánál vizsgáltuk, ahol T a gerjesztési jel periódus ideje.
U.I.:Az ilyen jellegű kérdéseket melyik "témában" tehetem fel???
|
|
| [210] Wolf | 2005-11-05 18:12:23 |
 Nagyon szépen köszönöm a segítségét... Tudnillik ezt a módszert villamosságtanban használjuk és sajnos nincs elég idő az adott módszerek megértéséhez csupán csak a használatához és ez ahhoz vezet,hogy a fiatal mérnökök az életben már nem is fogják használni, egyrészt nincs rá szükségük (munkahelyi feladatkör), másrészt meg se marad nekik a tanult anyag. Nem értem mi a célja a mérnökképzéseknek,ha nem az,hogy a tanult anyagokat rögzítsék a hallgatóságban és jólképzett mérnököket adjanak ki a kezükből. Mindenkinek még nekem is utána kell járnom bizonyos témákban ismereteket szerezni, különben nem fogunk semmit megérteni csupán "néhány órás" szemináriumokon.
|
| Előzmény: [209] Lóczi Lajos, 2005-11-04 20:46:17 |
|
| [209] Lóczi Lajos | 2005-11-04 20:46:17 |
 Ezzel kapcsolatban a következők jutottak eszembe. A Fourier- és Laplace-transzformációkkal szoktunk az integráltranszformációk közül leggyakrabban találkozni. Ha a transzformálandó függvény a negatív számokon nem érdekes (pl. azonosan nulla), akkor jó a Laplace-transzformációt alkalmazni. Továbbá, ha a függvény a plusz végtelen felé haladva nem csökken elég gyorsan, akkor a Fourier-transzformációban szereplő integrál esetleg nem lesz konvergens. Ekkor is előnyös a Laplace-tr., amely tehát egyfajta súlyozott Fourier-tr.-ként fogható fel: a súlyfüggvény az exponenciális függv. Mivel ez gyorsan csökken, az integrált konvergenssé teheti, akár még exponenciálisan gyorsan növő f-ek esetén is. (Az a bizonyos s a súlyfüggvény kitevőjében a Laplace-transzformáció konvergenciafélsíkjának szélét határozza meg.)
A Laplace-tr. tipikus alkalmazásai közé tartozik bizonyos differenciálegyenletek megoldása. A diff. egyenletet transzformálva egy "algebrai" egyenletet kapunk. Ennek megoldását kell vissza-Laplace-transzformálni, hogy megkapjuk az eredeti diff. egyenlet megoldását. Nyilván ez utóbbi lépés a legnehezebb, ezen múlik a módszer sikere és alkalmazhatósága.
|
| Előzmény: [208] Wolf, 2005-11-04 11:43:09 |
|
| [208] Wolf | 2005-11-04 11:43:09 |
 Üdvözletem!!!
Elnézést, gondolhattam volna... Tehát arra vagyok kiváncsi, ha az időfv.-em w körfrekvencia szerint változik, akkor a fv. Laplace-transzformáltja a komplex számsíkon ábrázolható.Ennek a transzformálásnak mi a jelentősége, hogy kell elképzelni? Mivel a sin(wt) L.Tr.-ja valós részű, és a cos(wt) L.tr.-ja képzetes részű, akkor ezek kombinációival (pl.:Fourier-sor) egy jelleggörbét kapok a kompl.sz.-on? Ezen vektorok jellemzéséből utaltam az e(-st) tagra, melyett mindig fel kell használni... Mit befolyásol ez a tag a transzformálás során, mi az "s"? Sajnos nincs kellő átlátásom az adott témáról, elnézést ha éppenséggel "hülyeséget" írtam. Tudom kicsit már fizika, de nagy szükségem lenne a segítségére, köszönöm!!!
|
| Előzmény: [200] Lóczi Lajos, 2005-11-01 20:52:53 |
|
| [207] Lóczi Lajos | 2005-11-03 22:17:18 |
 A levezetés nekem sosem kellett, csak a formulákat használtam (többdimenziós esetben). Hallottam, hogy ezek a formulák szoros kapcsolatba hozhatók kombinatorikus fákkal és gráfokkal, tehát ilyen könyvekben is keresgélhetsz.
|
| Előzmény: [206] Tibi, 2005-11-03 08:31:26 |
|
| [206] Tibi | 2005-11-03 08:31:26 |
 Keressgettem és találtam is valamit a levezetésről, de én másképp oldottam meg: teljes indukcióval. Csinálta más is?
|
|
| [205] Tibi | 2005-11-03 08:12:56 |
 Az ok, hogy a formulák nyelvfüggetlenek, de engem a képlet bizonyítása érdekelne...magyarul.Nem tudod, merre találhatnám meg?Egyáltalán benne van ez valamilyen tankönyvben?
|
| Előzmény: [204] Lóczi Lajos, 2005-11-02 22:09:15 |
|
|
|
|
| [201] Tibi | 2005-11-02 21:03:20 |
 Sziasztok!
Lehet, hogy most butaságot fogok kérdezni, de tud valaki képletet az összetett függvények magasabbrendű deriváltjainak előállítására? Én egy könyvben sem találok ilyet. Köszönöm a választ!
|
|
|
| [199] Lóczi Lajos | 2005-11-01 20:50:38 |
 http://mathworld.wolfram.com/LaplaceTransform.html
igaz, hogy angol, de a képleteket lehet érteni. Néhány függvény Laplace-transzformáltja benne van. (Esetleg konkrétabb kérdést is megfogalmazhatsz itt, miután elolvastad és megpróbálunk válaszolni rá.)
|
| Előzmény: [198] Wolf, 2005-11-01 20:39:02 |
|
| [198] Wolf | 2005-11-01 20:39:02 |
 Üdvözletem!!!
Szeretném megkérdezni, hogy a Laplace-transzformáció tulajdonképpen miről szól és mit jelent az F(s)=integral[F(t)e(-st)1(t)dt] alakból az exponenciális tag, ahol 1(t) az egységugrás és 0-infinity intervallumban vizsgáljuk? Esetleg hol tudok ennek utánanézni(magyar leírás)?
U.i.: Bocs, hogy így adtam meg... Köszönöm
|
|




 1, bizonyítsuk be ekkor, hogy Fn=22n+1 ( azaz az n-edik Fermat szám ) prím akkor és csak akkor, ha az S0=5 és Sk+1=Sk2-2 rekurzióval definiált sorozat esetén az S2n-2 osztható Fn-nel.
1, bizonyítsuk be ekkor, hogy Fn=22n+1 ( azaz az n-edik Fermat szám ) prím akkor és csak akkor, ha az S0=5 és Sk+1=Sk2-2 rekurzióval definiált sorozat esetén az S2n-2 osztható Fn-nel. között az a kapcsolat, amit írtál, akkor ez jön ki. (De ugyanezt az eredményt írtad az eredeti kérdésedben is, tehát nem kell meglepődni.)
között az a kapcsolat, amit írtál, akkor ez jön ki. (De ugyanezt az eredményt írtad az eredeti kérdésedben is, tehát nem kell meglepődni.)
 Re?
Re?  1;
1; i alakú számok, ahol i a képzetes egység és k tetszőleges egész. (Ez pedig lényegében az Euler-formulán múlik, miszerint
i alakú számok, ahol i a képzetes egység és k tetszőleges egész. (Ez pedig lényegében az Euler-formulán múlik, miszerint  tetszőleges (komplex vagy valós) szám.)
tetszőleges (komplex vagy valós) szám.)