| [317] Károly | 2006-07-12 21:08:21 |
 Jó, nem bizonyítás...:-)) Hanem csak egy gondolatmenet, amely arra utal, hogy nincsenek 2-vel és 3-mal osztható elemszámú véges struktúrák.
A gondolatmenet arra épül, hogy ha ez a struktúra egy Abel-csoportból képződik
ac=b  ac=b2 ac=b2
definícióval, akkor a csoport rendje, amelyből létrejön, nem lehet 2-vel vagy 3-mal osztható. Csakhogy - amint az Általatok bemutatott példák illusztrálják - nem csak csoportból jöhet létre ilyen struktúra. A +n-es "visszacsinálási" módszer sem megy minden ilyen táblára, a +n ugyanis nem lesz feltétlenül asszociatív.
Ettől függetlenül lehetséges, hogy a 2-vel vagy 3-mal oszthatóság tilalma öröklődik ezekre a táblákra, de ezt még nem tudom.
Károly
|
| Előzmény: [316] Károly, 2006-07-11 21:38:19 |
|
|
| [315] lgdt | 2006-07-11 21:26:05 |
 Köszi. Úgy néz ki, hibás volt a kódom. Elvileg az enyém is megtalálta volna az összes lehetőséget. :) Most bizonyítsuk be vagy cáfoljuk meg, h nincs páros elemszámú!
|
|
|
| [313] Károly | 2006-07-11 17:42:40 |
 Bocs, közben rájöttem, hogy hogy kell nézni... A fejléc mindenütt 0, 1, ... n - 1. Látom a táblákról, hogy idempotensek, kommutatívak, regulárisak. A hurokmentességet kapásból nem látom, de biztos úgy van. Akkor ezek ellenpéldák, és köszönöm.
Károly
|
| Előzmény: [311] lgdt, 2006-07-11 16:45:41 |
|
| [312] Károly | 2006-07-11 17:19:44 |
 Milyen szabályokkal hoztad létre ezeket a struktúrákat? Ha jól olvasom őket (nem biztos, hogy jól olvasom, mert fej- és oldalléceket nem látok), ezek a struktúrák nem idempotensek.
Károly
P.S.: Használsz valamilyen matematikai programot, vagy ez egy SQL-eredmény?
|
| Előzmény: [311] lgdt, 2006-07-11 16:45:41 |
|
| [311] lgdt | 2006-07-11 16:45:41 |
 Nekem most úgy tűnik, hogy nem igaz (az asszociativitás hiányából nem következik, hogy ez van helyette).
Itt van 8-ig az összes véges struktúra, hételemű a legelső, amire nem teljesül az állítás. Kérlek, ellenőrizz le egy ellenpéldát, hogy biztosan nem értettem-e félre valamit.
De vajon az igaz, hogy csak páratlan elemszámú ilyen struktúra létezik a végesek között?
|
| Előzmény: [310] Károly, 2006-07-10 21:05:50 |
|
|
|
| [308] Károly | 2006-07-09 17:17:55 |
 Kösz! Persze! "Elszámoltam" magam. Rossz szelektet írtam (ezeket a táblákat SQL-ben nézegetem).
Vagyis a +n visszaadja az 5-elemű ciklikus csoportot, melynek egységeleme n.
Ez már olyan, mintha lenne egy tételünk...:-))
Szerinted az axiómákból le lehet-e vezetni, hogy (ab)(ac)=b(ac) vagy esetleg van ellenpélda?
(Vagy, ami ezzel szorosan összefügg: be lehet-e bizonyítani, hogy az ab létezik definícióval adott reláció ekvivalenciareláció?)
Még egyszer nagyon köszönöm, hogy kijavítottál.
Üdv
Károly
|
| Előzmény: [307] 2501, 2006-07-09 16:01:49 |
|
| [307] 2501 | 2006-07-09 16:01:49 |
 Szervusz!
Szerintem elszámoltál (illetve "-betűztél" :)) valamit. Az a+nb=c  a*b=c*n definícióból következik, hogy a+nzn=a a*b=c*n definícióból következik, hogy a+nzn=a  a*zn=a*n (ahol zn az egység). Ebből már következik, hogy zn=n, feltéve, hogy az fa(b)=a*b függvény injektív. a*zn=a*n (ahol zn az egység). Ebből már következik, hogy zn=n, feltéve, hogy az fa(b)=a*b függvény injektív.
|
| Előzmény: [306] Károly, 2006-07-07 19:28:39 |
|
| [306] Károly | 2006-07-07 19:28:39 |
 Neeem!
Nagyon örülök, hogy rögtön vágtad.
Mutatok egy nemtriviális véges példát:
|
a |
b |
c |
d |
e |
| a |
a |
d |
b |
e |
c |
| b |
d |
b |
e |
c |
a |
| c |
b |
e |
c |
a |
d |
| d |
e |
c |
a |
d |
b |
| e |
c |
a |
d |
b |
e |
|
(Húú - régen TeX-eltem...!! :-)
Ez a tábla természetesen a mod 5 additív csoportból készült - úgy, ahogy mondtad - átlagokkal.
Namost. Vissza lehet-e kapni ebből az algebrai struktúrából az 5-elemű ciklikus csoportot?
A gondolatmenet a következő: Vezessük be erre a szorzótáblára építve az a+nb műveletet, melynek eredménye c, ha ab=cn (a szorzatokat itt az én táblámban kell leolvasni). Az n természetesen a struktúra egyik rögzített eleme.
Az eljárás szépen vissza is adja az 5-elemű ciklikus csoportot. Eddig csupa derű. Csakhogy: melyik elem lesz az így visszakapott ciklikus csoport egységeleme?
Ha erre a kérdésre az átlaggal kívánsz választ adni, a következőt mondod: Most
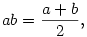
tehát
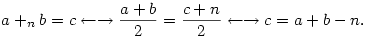
Az így kapott művelet
asszociatív, mert (a+nb)+nc=a+b+c-2n
egységelemes, egységelem az n, mert a+nn=a+n-n=a
invertálható, a inverze 2n-a
és kommutatív (ami triviális), tehát tényleg Ábel-csoport.
És - figyelem - egységeleme az n.
Na ezzel szemben ennek a táblának a származtatott +n-je így viselkedik:
| Ha n = |
a |
b |
c |
d |
e |
| akkor az egységelem |
a |
e |
d |
c |
b |
|
Vagyis az egységelem nem n, hanem az nx=a egyenlet megoldása (úgy is írhatnám ez esetben, hogy an-1.
Honnan van a-nak ez a kitüntetett szerepe? Úgy érzem, a táblázat teljesen szimmetrikus az öt betűre nézve. Vagy elszámoltam valamit?
Köszönöm
Károly
|
| Előzmény: [305] 2501, 2006-07-07 10:24:38 |
|
|
| [304] Károly | 2006-07-07 09:21:00 |
 Más: Ti hogy tanultátok a definíciót?
f felbonthatatlan, ha f = ab-ból az következik, hogy vagy f és a vagy f és b asszociáltak.
Avagy
f felbonthatatlan, ha f = ab-ből az következik, hogy vagy a vagy b egység.
Köszönöm
Károly
|
|
| [303] Károly | 2006-07-07 09:19:22 |
 Abbahagyva a hülyéskedést, én eddig a következőket látom:
(1) Ha a struktúra véges, akkor (1.a) A 2. axióma sima kommutativitásba megy át. (1.b) A 4. axióma tétel.
(2) Az 5. axióma független, mert van nemtriviális példa 1-4-re, úgy, hogy 5. nem teljesül.
Kösz
Károly
|
| Előzmény: [300] Károly, 2006-07-06 16:18:33 |
|
| [302] Károly | 2006-07-07 09:02:34 |
 Nem úgy értettem, hogy mondjatok példát. (A példa egyébként jó.:-) Hanem úgy, hogy valaki azt mondja, hogy igen, van ilyen algebrai struktúra, korbácsnak hívják, és Vittorio d'Assistenza olasz matematikus publikált tételeket a Zeitschrift der angewandten Nabelschau-ban.
Károly
|
| Előzmény: [301] 2501, 2006-07-06 23:26:24 |
|
|
| [300] Károly | 2006-07-06 16:18:33 |
 Sziasztok!
Új vagyok, ha nem jó helyen járok, irányítsatok át!
Szükségem lenne egy algebrai struktúrára, a következő axiómákkal:
1. Idempotencia: aa = a 2. "Kommutativitás": ab =?= ba (Ezt a jelölést én találtam ki; olvasd: ab, ha létezik, egyenlő ba-val. Ez amolyan "kváziművelet", nem minden ab létezik, de ha létezik, akkor ba is létezik, és egyenlő ab-vel.) 3. Megoldhatók x-re az ax = b egyenletek. 4. Az ax = a egyenlet egyetlen megoldása: x = a. 5. Hurokmentesség: (ab = c és ac = b) => b = c (És ekkor már a = b = c.)
(Asszociativitás nincs!)
Ráismertek-e valami hasonlóra? Van-e neve? Vannak-e tételek?
Köszönöm
Károly
|
|
| [299] joe | 2006-06-02 19:48:53 |
 138. feladat: (Ha nem tévedek.)
Azt mondjuk, hogy a k számot öröklődő n alapú számrendszerben írjuk föl, ha a k számot a következőképpen fejezzük ki: Írjuk föl a k számot (a hagyományos módon) n alapú számrendszerben, majd az együtthatókat "fejtsük ki", tehát 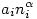 helyett írjunk ai darab összeadandót: helyett írjunk ai darab összeadandót: 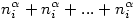 . Az így kapott kifejezésben minden kitevőt írjunk öröklődő n alapú számrendszerbe (tehát ismételjük meg az n alap minden kitevőjére az imént leírt eljárást; majd a kitevőkben szereplő számok kitevőire, és így tovább). Ezt az eljárást addig folytatjuk, amíg a kifejezésben csak a + jel, az n szám és a 0 szerepel (tehát az 1-et n0 -nak írhatjuk). Ez a rekurzív eljárás véges sok lépésben véget ér, és a k szám egyértelmű öröklődő n alapú számrendszerbeli alakját adja. . Az így kapott kifejezésben minden kitevőt írjunk öröklődő n alapú számrendszerbe (tehát ismételjük meg az n alap minden kitevőjére az imént leírt eljárást; majd a kitevőkben szereplő számok kitevőire, és így tovább). Ezt az eljárást addig folytatjuk, amíg a kifejezésben csak a + jel, az n szám és a 0 szerepel (tehát az 1-et n0 -nak írhatjuk). Ez a rekurzív eljárás véges sok lépésben véget ér, és a k szám egyértelmű öröklődő n alapú számrendszerbeli alakját adja.
Definiáljuk a következő sorozatot: a0:=k, ahol k természetes szám;
Minden i természetes számra:
Ha ai-1 nem pozitív egész, a sorozatnak nincs több tagja.
Ha ai-1 pozitív egész, akkor írjuk föl azt öröklődő i+1 alapú számrendszerben; az így kapott kifejezésben MINDEN (i+1) számot cseréljünk ki (i+2)-re, számítsuk ki az így keletkezett kifejezés értékét, és az ennél eggyel kisebb számérték legyen ai.
Melyek azok a k természetes számok, melyekre a0=k esetén az ai sorozat véges?
|
|
|
| [297] Lóczi Lajos | 2006-05-25 15:07:12 |
 A
http://mathworld.wolfram.com/CoinTossing.html
http://mathworld.wolfram.com/Run.html
http://mathworld.wolfram.com/Fibonaccin-StepNumber.html
oldalakon mindenféle szép rekurziókat meg generátorfüggvényeket fogsz találni olyan kérdésekről, hogy pl. "mennyi az esélye, hogy n dobásban nincs k egymásutáni írás", vagy hogy "mennyi az esélye, hogy egy n hosszú dobássorozatban előfordul egy legalább k hosszúságú fejsorozat".
|
| Előzmény: [296] stephen, 2006-05-25 10:04:42 |
|
| [296] stephen | 2006-05-25 10:04:42 |
 Nagyon érdekelne az alábbi feladat megoldása:
Feldobunk n pénzérmét. Mennyi a valószínűsége, hogy lesz legalább k egyforma (fej vagy írás) egymás mellett?
|
|
| [295] nadorp | 2006-04-07 08:54:40 |
 Köszi a gyors választ és a cikket. "Tisztességes" primitív függvény létezésében én sem hittem, de gondoltam, hátha vannak itt is olyan speciális integrálási határok, ahol az érték meghatározható valamilyen módszerrel ( paraméteres integrál, komplex integrál stb,mint pld. 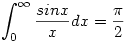 esetén) esetén)
|
| Előzmény: [292] Lóczi Lajos, 2006-04-07 00:52:18 |
|
| [294] Lóczi Lajos | 2006-04-07 01:48:32 |
 Homogenitásvizsgálatot alkalmaznak akkor, ha azt szeretnék eldönteni, hogy a két minta azonos eloszlásból származik-e, de maga az eloszlás ismeretlen.
Ha tudjuk, hogy normális eloszlásból származnak a minták és ezek egymástól függetlenek, kétmintás próba alkalmazható: ha a szórás nem ismert, de feltehető, hogy azonos, akkor használnak kétmintás t-próbát.
|
| Előzmény: [290] rizsesz, 2006-03-21 11:15:30 |
|
|




 ac=b2
ac=b2

 a*b=c*n definícióból következik, hogy a+nzn=a
a*b=c*n definícióból következik, hogy a+nzn=a 
