| [341] Sirpi | 2006-09-08 22:17:26 |
 Ja, én is ezt ismerem. Amúgy fel szokták úgy is adni, hogy számológépen kell a megfelelő számot kihozni és azokon általában nincs log2 függvény, mondjuk a log2x=(log x)/log 2 azonossággal áthidalható a probléma, ha akár 10-es, akár természetes alapú logaritmust jelöl a törtben szereplő log (tudom, túlragoztam).
|
| Előzmény: [340] jonas, 2006-09-08 00:23:26 |
|
|
| [339] rizsesz | 2006-09-07 22:29:04 |
 Egy gyors közbeékelés: Ezt is hallottam, de a megoldását nem ismerem:
Adott 3 darab kettes. A középiskolában tanult függvényekkel ezekből bármely pozitív egész előállítására alkalmas módszert keresünk.
|
|
|
|
| [336] Lóczi Lajos | 2006-08-28 17:39:00 |
 Szerintem ezek egyike sem megoldás. Gondolom, ugyanazt a hibát követted el, mint én (ezekkel a függvényekkel már én is dolgoztam, és azért nem megoldások, mert u(x2,t) áll a második tagban, tehát ez nem is differenciálegyenlet a szokásos értelemben).
|
| Előzmény: [335] Cckek, 2006-08-28 13:33:03 |
|
|
| [334] Sirpi | 2006-08-28 11:26:19 |
 Tudom, lényegi részre tapintottam rá (és bocs a kukacoskodásért), de a ugye jól gondolom, hogy a beolvasztható b-be és c-be, ezért nincs is rá szükség?
|
| Előzmény: [333] Cckek, 2006-08-28 09:40:47 |
|
|
| [332] Cckek | 2006-08-26 19:11:35 |
 Ugyanis, ha u(x,t)=f(x)g(t)
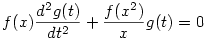 . .
Az y"+y=0 egyenlet megoldásai az: y=c.sin(t)+d.cos(t) s igy csak azokat a függvényeket keressük melyekre:
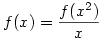 , ,
f(0)=0 s ezek nyilván az f(x)=ax R-beli lineáris függvények
|
| Előzmény: [331] Lóczi Lajos, 2006-08-26 17:55:41 |
|
|
| [330] Cckek | 2006-08-26 00:39:29 |
 Nagyon érdekes, köszönöm. Esetleg olyan megoldás mely nem szétválasztható változójú?
|
|
|
| [328] Cckek | 2006-08-25 19:30:43 |
 A következő memlineáris differenciálegyenlet megoldhatósága érdekel,bármilyen határok között:
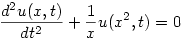
|
|
|
|
| [325] Károly | 2006-07-21 16:19:02 |
 Hm... nadorp, első ránézésre úgy tűnik, igazad van. Meg a másodikra is.
Valami nem stimmel nekem. Én erre emlékszem: "To every polynomial f in R[X], one can associate a polynomial function with domain and range equal to R. One obtains the value of this function for a given argument r by everywhere replacing the symbol X in f's expression by r. The reason that algebraists have to distinguish between polynomials and polynomial functions is that over some rings R (for instance, over finite fields), two different polynomials may give rise to the same polynomial function. This is not the case over the real or complex numbers and therefore many analysts often don't separate the two concepts." (Forrás: Wikipedia "Polynomial" szócikk.)
Mit zagyválok össze?
Meg egyébként is: a "véges testekben minden függvény polinom" annyira alapvető állításnak tűnik, miért nem szaladtam bele eddig? Csak elbambultam?
Üdv
Károly
|
| Előzmény: [324] nadorp, 2006-07-20 18:12:56 |
|
| [324] nadorp | 2006-07-20 18:12:56 |
 Kedves Károly !
Ott tévedsz el, hogy GF(4) felett 43=64 polinom van. Nem igaz, mert a polinomok legmagasabb kitevője 3 és nem 2 lehet. Az ellentmondásnak az az oka, hogy Te felteszed az x3=1 azonosságot, holott x=0 esetén nem igaz ( más szavakkal pld az x3+x+1 polinom nem egyenlő az 1+x+1=x+2 polinommal). A harmadfokú polinomok száma pedig 44=256, tehát nincs semmilyen ellentmondás.
|
| Előzmény: [323] Károly, 2006-07-20 14:10:13 |
|
| [323] Károly | 2006-07-20 14:10:13 |
 Kedves nadorp!
Köszönöm a pontosítást. Ami a lényeg: pk elemű testben kevesebb polinom van, mint ahány függvény. Pl. GF(4)-ben 64 polinom van (itt eltévesztettem egy kitevőt, hiszen 2 a legmagasabb fokszám), ugyanakkor 256 függvény van, mert GF(4) 4-elemű halmaz. Ezért gondolom, hogy nem lehet minden függvény polinom.
Károly
|
| Előzmény: [322] nadorp, 2006-07-20 09:28:14 |
|
| [322] nadorp | 2006-07-20 09:28:14 |
 A karakterisztika azt jelenti, hogy a test egy x elemére nx=0 teljesül és n a legkisebb ilyen tulajdonságú pozitív egész ( véges testben persze a karakterisztika prím), nem azt, hogy xp-1=1. Ha q=pk, akkor minden nem 0 elemre xq-1=1
http://mathworld.wolfram.com/FiniteField.html
|
| Előzmény: [321] Károly, 2006-07-19 17:58:17 |
|
| [321] Károly | 2006-07-19 17:58:17 |
 Bocs, lehet, hogy nem jól értek valamit: miért van az, hogy "véges test fölött minden függvény polinom"? Én úgy számolok, hogy ha egy véges test elemszáma pk, akkor a test fölött (pk)pk függvény van. De minden elem karakterisztikája p, ezért a legmagasabb fokszámú polinom p-1-edfokú. Ezekből pedig (pk)p db - azaz sokkal kevesebb - van.
Üdv
Károly
|
| Előzmény: [120] jonas, 2005-01-13 17:21:23 |
|
| [320] Károly | 2006-07-14 08:38:04 |
 Köszönöm a bizonyítást!
Nevezzük az idempotens, kommutatív, reguláris és hurokmentes táblákat K-tábláknak, hogy tudjunk róluk beszélni! Az eddigiek szerint
1. Ha G olyan 1-nél több elemű Abel-csoport, hogy a2=b2 a=b és a3=b3 a=b és a3=b3 a=b, akkor a G-ből képzett a=b, akkor a G-ből képzett 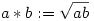 művelet K-tábla. Az ilyen csoport neve legyen E-csoport! művelet K-tábla. Az ilyen csoport neve legyen E-csoport!
2. Véges E-csoportok elemszáma nem lehet 2-vel illetve 3-mal osztható, mert ebben az esetben van bennük 2- ill. 3-elemű direkt osztó, amelyben a2=b2 ill. a3=b3 úgy, hogy a b. Azaz, ha a K-tábla ilyen csoportból keletkezik, akkor elemszáma nem lehet 2-vel vagy 3-mal osztható. b. Azaz, ha a K-tábla ilyen csoportból keletkezik, akkor elemszáma nem lehet 2-vel vagy 3-mal osztható.
3. Ha a K-tábla E-csoportból keletkezik, a +n művelettel (a+nb=c  a*b=c*n) visszakapjuk az E-csoport egy izomorf képét, a képben az egységelem az n. a*b=c*n) visszakapjuk az E-csoport egy izomorf képét, a képben az egységelem az n.
4. Vannak nem E-csoportból származó K-táblák. Az ilyen (véges) K-táblák elemszáma továbbra sem lehet páros, 3-mal osztható viszont igen.
5. A (4) pontban említett K-táblák esetében a +n művelet nem asszociatív, és (a*b)*(b*c)=b*(a*c) sem teljesül.
Ezek igazak?
Üdv
Károly
|
| Előzmény: [319] 2501, 2006-07-13 20:13:37 |
|
| [319] 2501 | 2006-07-13 20:13:37 |
 Tétel: nincs páros elemszámú ilyen struktúra.
Biz.: Próbáljuk megadni az a*b = c műveletet az Ma,b = c mátrix kitöltésével (ahogyan az [311]-ben és [314]-ben látható). A művelet idempotens (1), tehát az (a=b) átlót teljesen kitöltjük: M0,0 = 0, M1,1 = 1 stb. A művelet kommutatív (2), és megoldhatók az a*x = b egyenletek (3), tehát a mátrix az átlóra szimmetrikus, és minden sorban illetve oszlopban minden érték pontosan egyszer szerepel. Ezért az első (jobban mondva 0.) sor illetve oszlop elhagyásával kapott részmátrixban el kell még helyeznünk annyi 0-t, amennyi sora (illetve oszlopa) van, tehát páratlan számút. Ahhoz viszont, hogy a mátrix szimmetrikus legyen, páros számú 0-t kellene elhelyeznünk, mivel az átló már teljesen be van töltve. Ez ellentmondás, a mátrixot nem lehet kitölteni, tehát a művelet nem létezik páros elemszámú struktúrán.
|
| Előzmény: [300] Károly, 2006-07-06 16:18:33 |
|
|
| [317] Károly | 2006-07-12 21:08:21 |
 Jó, nem bizonyítás...:-)) Hanem csak egy gondolatmenet, amely arra utal, hogy nincsenek 2-vel és 3-mal osztható elemszámú véges struktúrák.
A gondolatmenet arra épül, hogy ha ez a struktúra egy Abel-csoportból képződik
ac=b  ac=b2 ac=b2
definícióval, akkor a csoport rendje, amelyből létrejön, nem lehet 2-vel vagy 3-mal osztható. Csakhogy - amint az Általatok bemutatott példák illusztrálják - nem csak csoportból jöhet létre ilyen struktúra. A +n-es "visszacsinálási" módszer sem megy minden ilyen táblára, a +n ugyanis nem lesz feltétlenül asszociatív.
Ettől függetlenül lehetséges, hogy a 2-vel vagy 3-mal oszthatóság tilalma öröklődik ezekre a táblákra, de ezt még nem tudom.
Károly
|
| Előzmény: [316] Károly, 2006-07-11 21:38:19 |
|







 R
R


 b. Azaz, ha a K-tábla ilyen csoportból keletkezik, akkor elemszáma nem lehet 2-vel vagy 3-mal osztható.
b. Azaz, ha a K-tábla ilyen csoportból keletkezik, akkor elemszáma nem lehet 2-vel vagy 3-mal osztható. 
 a*b=c*n) visszakapjuk az E-csoport egy izomorf képét, a képben az egységelem az n.
a*b=c*n) visszakapjuk az E-csoport egy izomorf képét, a képben az egységelem az n. 