|
| [351] rizsesz | 2006-09-25 18:06:09 |
 2 remek stratégia-alkotó feladat:
a., adott 4 város, melyek egy 20 egység oldalú négyzet sarkaiban vannak. lehetőségünk van 55 km út kiépítésére, de többre nem. ezek segítségével kiépíthető olyan út-rendszer, melyeken bármely városból bárhova el lehet-e jutni? b., Egy kirándulónk egy félsík alakú erdőben tévedt el. Ismert, hogy legfeljebb 6km-t tett meg az. A maratoni távnál kisebb séta alatt ki tud-e jutni, magyarul a legrosszabb esetben is olyan stratégiája van, hogy kijut.
|
|
| [350] jonas | 2006-09-18 13:45:23 |
 Nem is tudom.
Először is  amiből 2x=1/((1/x)/2) amiből pedig x2=exp(2log x) tehát a négyzetreemelést pontosan el tudjuk végezni. amiből 2x=1/((1/x)/2) amiből pedig x2=exp(2log x) tehát a négyzetreemelést pontosan el tudjuk végezni.
Ha lenne 2 alapú logaritmusunk és exponensünk is, akkor most egyszerű dolgunk lenne:
n=log2(2.2...2.2.1)
1=2n/2/2/.../2/2
|
| Előzmény: [349] rizsesz, 2006-09-18 13:00:49 |
|
| [349] rizsesz | 2006-09-18 13:00:49 |
 a [342]-es hozzászólásomra nincsen valakinek valami remek ötlete?
|
|
|
|
| [346] lorantfy | 2006-09-17 20:17:58 |
 Szia Atlas!
Ha levágod a gúla tetejét az alappal párhuzamos síkkal az is egy gúla lesz és hasonló az eredeti gúlához.
A térfogatok aránya, ami 1/2, a hasonlóság arányának köbével egyenlő. Így a magasságok aránya ennek köbgyöke.
Ennek fordítotja: Ha a magassága feléig töltünk egy kúp alakú pezsgőspoharat akkor valójában meddig van pezsgővel?
|
| Előzmény: [345] Atlas1458, 2006-09-17 16:09:25 |
|
| [345] Atlas1458 | 2006-09-17 16:09:25 |
 Hello. Tudom hogy nem nehéz a feladat( nem pont ide tartozik), de nekem nem nagyon akar menni. Hol metszünk el egy négyzet alapú egyenes gúlát az alaplappal párhuzamos síkkal, hogy a térfogatát megfelezzük?
|
|
| [344] Gubbubu | 2006-09-10 23:21:33 |
 Na, kezdem érteni. Elnézést, a fordítás első mondatát kicsit elhibáztam az előbb: nem arról van szó, hogy R[X] a valós számok teste feletti polinomgyűrűt jelölné, és hogy egy-egyértelműen tartozna minden polinomfüggvényhez polinom. A cikkíró itt nyilván csak arra gondol, hogy ha már van egy polinomod, akkor abba rendre bepötyögve a gyűrű elemeit, egy függvényt kapsz, ami (minthogy polinommal számoltad ki az értékeit) polinomfüggvény.
|
| Előzmény: [343] Gubbubu, 2006-09-10 11:32:57 |
|
| [343] Gubbubu | 2006-09-10 11:32:57 |
 "To every polynomial f in R[X], one can associate a polynomial function with domain and range equal to R. One obtains the value of this function for a given argument r by everywhere replacing the symbol X in f's expression by r. The reason that algebraists have to distinguish between polynomials and polynomial functions is that over some rings R (for instance, over finite fields), two different polynomials may give rise to the same polynomial function. This is not the case over the real or complex numbers and therefore many analysts often don't separate the two concepts." (Forrás: Wikipedia "Polynomial" szócikk.)
A lényeg fordítása: a valós számok teste felett minden polinomhoz - halmazuk jele R[x] - (egy-egyértelműen - megjegyzés tőlem) tartozik egy polinomfüggvény. A legpihentebb agyú matematikusok szerint az x határozatlan helyére az r változójel írandó, de az ilyesmit nem kell komolyan venni, (ti. amíg végtelen test felett dolgozunk - megjegyzés ismét tőlem). Viszont más a helyzet az algebrában: itt meg kell különböztetni a polinomokat és polinomfüggvényeket, mert akadnak olyan R gyűrűk (itt zavaró, hogy e kontextusban R már nem a végtelen valós számokat, hanem tetszőleges gyűrűt jelölhet; nem tudom, az eredeti szövegben is így van-e - megjegyzés tőlem), különösképp ilyen R gyűrűk a véges testek - ahol két különböző polinomhoz már ugyanaz a polinomfüggvény tartozik (tehát: itt megbomlik az egy-egyértelműség, már nem mondható, hogy egy polinomfüggvényt megadva egyben egy polinomot is megadunk, hisz általában végtelen sokat adunk meg - ha jól emlékszem Gonda János "véges testek" előadására, melynek pdf-je valahol fenn van a neten, akkor az egy polinomfüggvényt képező polinomok valamilyen mod(x az akárhanyadikon+1) maradékosztályt alkotnak- duplazárójeles megjegyzés ismét tőlem). De ez a komplex számoknál ilyen nincs, mert ott lehetséges a polinomok azonosítása a polinomfüggvényekel, ld. bekezdés eleje (da capo al fine) ...
|
| Előzmény: [325] Károly, 2006-07-21 16:19:02 |
|
| [342] rizsesz | 2006-09-09 14:13:57 |
 egy ilyen feladatot is ismerek, melyben az van, hogy tetszőlegesen megadott két pozitív egész egyikéből kell eljutni a másikhoz. a számológép ismeri a köv. műveleteket: négyzet- és köbgyököt von, sinus, cosinus, tangens (mindezek hiperbolikus változatai is), 1/x, 10 és e alapú logaritmus, faktoriális. nincsenek viszont alapműveletek, se egyenlőség jel.
|
|
| [341] Sirpi | 2006-09-08 22:17:26 |
 Ja, én is ezt ismerem. Amúgy fel szokták úgy is adni, hogy számológépen kell a megfelelő számot kihozni és azokon általában nincs log2 függvény, mondjuk a log2x=(log x)/log 2 azonossággal áthidalható a probléma, ha akár 10-es, akár természetes alapú logaritmust jelöl a törtben szereplő log (tudom, túlragoztam).
|
| Előzmény: [340] jonas, 2006-09-08 00:23:26 |
|
|
| [339] rizsesz | 2006-09-07 22:29:04 |
 Egy gyors közbeékelés: Ezt is hallottam, de a megoldását nem ismerem:
Adott 3 darab kettes. A középiskolában tanult függvényekkel ezekből bármely pozitív egész előállítására alkalmas módszert keresünk.
|
|
|
|
| [336] Lóczi Lajos | 2006-08-28 17:39:00 |
 Szerintem ezek egyike sem megoldás. Gondolom, ugyanazt a hibát követted el, mint én (ezekkel a függvényekkel már én is dolgoztam, és azért nem megoldások, mert u(x2,t) áll a második tagban, tehát ez nem is differenciálegyenlet a szokásos értelemben).
|
| Előzmény: [335] Cckek, 2006-08-28 13:33:03 |
|
|
| [334] Sirpi | 2006-08-28 11:26:19 |
 Tudom, lényegi részre tapintottam rá (és bocs a kukacoskodásért), de a ugye jól gondolom, hogy a beolvasztható b-be és c-be, ezért nincs is rá szükség?
|
| Előzmény: [333] Cckek, 2006-08-28 09:40:47 |
|
|
| [332] Cckek | 2006-08-26 19:11:35 |
 Ugyanis, ha u(x,t)=f(x)g(t)
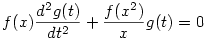 . .
Az y"+y=0 egyenlet megoldásai az: y=c.sin(t)+d.cos(t) s igy csak azokat a függvényeket keressük melyekre:
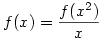 , ,
f(0)=0 s ezek nyilván az f(x)=ax R-beli lineáris függvények
|
| Előzmény: [331] Lóczi Lajos, 2006-08-26 17:55:41 |
|
|
| [330] Cckek | 2006-08-26 00:39:29 |
 Nagyon érdekes, köszönöm. Esetleg olyan megoldás mely nem szétválasztható változójú?
|
|
|
| [328] Cckek | 2006-08-25 19:30:43 |
 A következő memlineáris differenciálegyenlet megoldhatósága érdekel,bármilyen határok között:
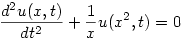
|
|










 R
R