| [38] Gubbubu | 2004-01-22 22:09:17 |
 Kedves László!
Még egy dolog eszembe jutott: szerintem tűzd ki e rovatban a programod által felvetett problémát (ti. keressük meg az összes nem nulla diszkriminánsú egész együtthatós másodfokú polinomot, ami az adott 4 helyen négyzetszámot ad, lássuk be, hogy véges/végtelen sok ilyen van stb.), vagy ha ez túl egyszerű, akkor valamiféle általánosítását (keressük meg az olyan stb. stb. polinomot, ami négy (szomszédos?) egész helyen négyzetszámot ad stb.). Én magam nem merem kitűzni, mivel tulajdonképp plágium lenne, de szívesen gondolkodnék rajta. Persze nem garantált, hogy meg is tudom oldani.
Üdvözöl: G.
|
| Előzmény: [35] lorantfy, 2004-01-22 21:32:40 |
|
| [37] Gubbubu | 2004-01-22 21:40:40 |
 Kedves László!
Csak most "kaptam meg" a hozzászólásodat. Mint az előbb említettem, ha a bizonyításom helyes, akkor a progid nem fog több "jó" polinomot találni. De ha mégis találsz, szólj, ez esetben megpróbálnám kiböngészni, hol rontottam el.
Üdvözöllek és kösz, hogy felhívtad a figyelmemet a figyelem nélküliségemre, vagyis a nemlétező figyelmemet arra, hogy nem létezik. G.
|
| Előzmény: [35] lorantfy, 2004-01-22 21:32:40 |
|
| [36] Gubbubu | 2004-01-22 21:33:10 |
 Kedves Pataki!
Bevettem néhány aszpirint, és eszembe jutott, hogy ki volt kötve D><0. A p(x) polinom diszkriminánsa véletlenül épp (-6)2-4.1.9=0. Azt azonban egyelőre (amíg még néhány gyógyszert be nem szedek) tartom, hogy nincs másik polionom, ami a többi feltételnek megfel. Tehát a válasz: szerintem nincs olyen polinom, amilyet keresel.
Üdvözlettel:M.Á.
|
| Előzmény: [34] Gubbubu, 2004-01-22 19:23:14 |
|
| [35] lorantfy | 2004-01-22 21:32:40 |
 Kedves Gubbubu!
Nem néztem át tüzetesen a levezetést, de az eredmény:
p(x)=x2-6x+9=(x-3)2
Ez "teljes négyzet", tehát minden értéke négyzetszám. A feladatban feltételként szerepelt, hogy a diszkrimináns ne legyen 0, tehát a kifejezés ne legyen teljes négyzet.
Én egyenlőre azt csináltam a témában, hogy írtam hozzá egy pár soros programot, de sajnos még olyan polinomot nem találtam ami mind az 5 helyen négyzetszám. Olyan van ami 4 helyen jó értéket ad (x=0,1,2,3-nál):
x2+498x+63 (36, 529, 1024, 1521) és párja
x2-498x+1521 (1521, 1024, 529, 36)
x2+3378x+1521 (1521, 4900, 8281, 11664) és párja
x2-3384x+11664 (11664, 8281, 4900, 1521) és
x2+7312x+256 (256, 7569, 14884, 22201).
Gondolom az utóbbinak is jó a "párja", csak egyenlőre +-12000-ig mentek az együtthatók. Ma majd kicsit gyorsítok a progin és lefottatom +-32000-ig.
|
| Előzmény: [34] Gubbubu, 2004-01-22 19:23:14 |
|
| [34] Gubbubu | 2004-01-22 19:23:14 |
 Kedves Pataki!
Nézd át tüzetesen az alábbiakat, hátha figyelmetlen voltam és hibás, szerintem van egyilyen polinom Mivel normált másodfokú egész együtthatós, p(x)=x2+bx+c legyen a polinom. Az előírt értékek alapján
I.p(0)=c=n12;
II.p(1)=1+b+c=n22;
III.p(2)=4+2b+c=n32;
IV.p(3)=9+3b+c=n42;
V.p(4)=16+4b+c=n52;
ahol b,c,ni Z; Az I. és II. egyenlet alapján Z; Az I. és II. egyenlet alapján
VI.b=(n22-n12-1)
Ezt a b-t most behelyettesítve III.-V.-be és összevonogatva az egyes egyenleteken belül az azonos nemű tagokat:
VII.2+2n22-n12=n32;
VIII.6+3n22-2n12=n42;
IX.12+4n22-3n12=n52;
Képezve a VIII.-VII.=X. és XI.-VIII.=XI. egyenleteket: X. 4+n22-n12=n42-n32; XI. 6+n22-n12=n52-n42; Kivonva XI.-ből X.-et: 2=(n52+n32);
Tehát két négyzetszám összege 2. Ez pedig nem túl sok lehetőség: 2 egyféleképp írható fel két egész szám négyzetösszegeként: 2=1+1. Tehát n5=n3=1; ezeket az értékeket visszahelyettesítve III.-ba és V.-be adódik a 4b+2c=1 és 16+4b+c=1 lineáris kétismeretlenes egyenletrendszer. Megoldva b=-6 és c=9.
Ha van ilyen polinom, az csak
p(x)=x2-6x+9
lehet. És: p(0)=9, p(1)=4, p(2)=1, p(3)=0, p(4)=1; ezek ha nem is mind "valódi" négyzetszámok, de azért annak mondhatóak.
De vizsgáztam ma és iszonyúan fáj a fejem, úgyhogy lehet, hogy rossz az egész, remélem nem.
Üdv: M.Á.
|
| Előzmény: [32] pataki, 2004-01-21 16:55:39 |
|
| [33] Gubbubu | 2004-01-21 19:50:55 |
 Kedves Lóczi Lajos!
Először is köszönöm a pontosításokat, illetve a megoldást. Véletlenül elírtam: valójában a negatív megoldások számomra nem érdekesek, elég az x R+ halmazon megoldani. A "folytonosított függvény" kifejezés nemhiába volt idézőjelben (egy kifejezés akkor lehet idézőjelben, ha idézet, vagy ha pontatlan). A mélyebb magyarázatba részben nem is akartam belemenni (ezt nehéz lenne fórumszöveg-terjedelemben véghezvinni), részben pedig nem is értek hozzá annyira (én magam nem tudnám megoldani, de szerintem ez nem ok arra, hogy egy feladat örökké az íróasztal fiókjában heverjen - úgy gondoltam, a feladat hangzik annyira érdekesen, hogy megérje kitűzni, vállalva a pontatlanság kockázatát is). R+ halmazon megoldani. A "folytonosított függvény" kifejezés nemhiába volt idézőjelben (egy kifejezés akkor lehet idézőjelben, ha idézet, vagy ha pontatlan). A mélyebb magyarázatba részben nem is akartam belemenni (ezt nehéz lenne fórumszöveg-terjedelemben véghezvinni), részben pedig nem is értek hozzá annyira (én magam nem tudnám megoldani, de szerintem ez nem ok arra, hogy egy feladat örökké az íróasztal fiókjában heverjen - úgy gondoltam, a feladat hangzik annyira érdekesen, hogy megérje kitűzni, vállalva a pontatlanság kockázatát is).
Üdv:G.
|
| Előzmény: [31] Lóczi Lajos, 2004-01-21 13:46:23 |
|
| [32] pataki | 2004-01-21 16:55:39 |
 Szeretnék olyan normált ( 1 fôegyütthatójú) egész együtthatós másodfokú polinomot, amelynek nem nulla a diszkriminánsa és a 0,1,2,3,4 helyeken négyzetszám az értéke. Vagy azt, hogy nincs ilyen.
|
|
| [31] Lóczi Lajos | 2004-01-21 13:46:23 |
 Először is pár megjegyzés: a gamma-függvényt definiáló integrálalak csak x>0 (illetve Re x>0, ahol Re a valós rész) esetén helyes. Negatív x-ekre a definíció más.
Másodszor a feladat kitűzésében nem szerencsés, hogy x jelöli mind az integrációs változót, mind az integrálás felső határát.
A "folytonosított függvény" kifejezés helyett a "folytonos kiterjesztés" a bevett szóhasználat. A faktoriális és a gamma függvény közötti kapcsolatban pedig vigyázni kell az indexeltolásra (aminek történeti okai vannak): n!= (n+1), ha n pozitív egész. (n+1), ha n pozitív egész.
Ezek után tehát az a kérdés, milyen valós x-ekre áll fenn, hogy
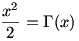
.
Pozitív x-ekre pontosan 2 megoldás van, az egyik kb. 1,33615, a másik kb. 4,34884. (Az, hogy van megoldás, folytonossági és határértéket tartalmazó meggondolásokból jön ki. A megoldások számához "kis" x-ekre konvexitási érvelés vezet, "nagy" x-ekre pedig az a tény, hogy a gamma-függvény viselkedése ilyen x-ekre ismert (Stirling-formula és társai), amiből látható, hogy a gamma-függvény sokkal "gyorsabban nő", mint bármely polinom, s így elég nagy x-ektől kezdve nincs megoldás.)
A gamma-függvénynek a nempozitív egészeknél pólusai vannak ("végtelenné válik"), az egyenletnek a negatív számok körében is vannak megoldásai, és a grafikonokat nézve számomra úgy tűnik, végtelen sok (melyek minden bizonnyal szintén nem adhatók meg rövidebb leírással, mint "a fenti egyenlet negatív megoldásai", numerikusan természetesen itt is bármelyiket akármilyen pontossággal ki lehet számolni, pl. egy negatív megoldás kb. -3,0347).
|
| Előzmény: [30] Gubbubu, 2004-01-20 19:26:37 |
|
| [30] Gubbubu | 2004-01-20 19:26:37 |
 Üdv mindenkinek!
Az "ujjgyakorlatok" c. témakörben szerepelt egy feladat: oldjuk meg a
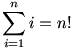
egyenletet!
Ennek a feladatnak a "folytonos analogonja" is kitűzhető (más kérdés, hogy akad-e valaki, aki megoldja:
13. fa. Oldjuk meg a
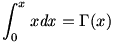
egyenletet (x R)! A gammafüggvény bizonyos értelemben a faktoriális "folytonosított függvénye": R)! A gammafüggvény bizonyos értelemben a faktoriális "folytonosított függvénye":
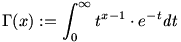
.
|
|
| [29] Gubbubu | 2004-01-16 21:59:49 |
 Kedves László:
A lényeget mindig elfelejtem! Igen, a  (n) a szám pozitív osztóinak összege, tehát (n) a szám pozitív osztóinak összege, tehát  (n)=1+d2+...+dd(n)-1+n, di az n osztói. (n)=1+d2+...+dd(n)-1+n, di az n osztói.
A "Számelméleti érdekességek" c. topikban definiáltam már ezt, itt még nem. Ezentúl nem csak itt, hanem minden számelméleti jellegű szövegben (ezt általában egyértelműen el lehet dönteni) ebben az értelemben fogom használni a  (n) jelet (minden hozzászólásomban azért mégse akarom mindig definiálni). Előfordulhat esetleg, hogy (n) jelet (minden hozzászólásomban azért mégse akarom mindig definiálni). Előfordulhat esetleg, hogy  valaminek a szórását jelöli, de ez a feladat szövegéből és képleteiből azért gondolom, kiderül majd. valaminek a szórását jelöli, de ez a feladat szövegéből és képleteiből azért gondolom, kiderül majd.
Üdv:G.
|
| Előzmény: [28] lorantfy, 2004-01-16 19:15:48 |
|
|
| [27] Gubbubu | 2004-01-16 18:55:52 |
 Üdv;
Egy határértékszámítási példa, remélem, jó nehéz lesz (ha nem, hát nem):
12. fa.: Jelölje Sn az n-edik háromszögszámot, más néven az első n természetes szám összegét. Igazoljuk, hogy
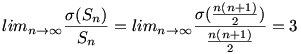
Megjegyzés: a határértéket részben empirikusan, részben a Derive programmal számoltam ki, így a feladat elvileg megoldható, és a benne foglalt állítás vsz. igaz.
|
|
| [26] Csizmadia Gábor | 2004-01-13 20:54:19 |
 A gyakorlatot vezető tanárodnak nagyon nem volt igaza, ugyanis a felső határ - akár elemi módszerekkel is - tetszőlegesen megközelíthető.
Gosztonyi Balázstól származik a következő megoldás.
Pozitív n,k,r számokra érvényes az alábbi mértani-számtani közép közti egyenlőtlenség:
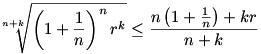
Válasszuk meg úgy k-t ér r-t, hogy a jobb oldal 1 legyen, ilyenkor:
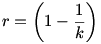
Visszaírva az eredeti kifejezésbe:
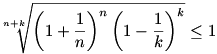
Ezután (n+k)-adik hatványra emelve, és kirendezve  -re: -re:
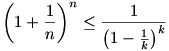
Pl. k=100 esetén
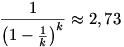
|
| Előzmény: [25] bbb, 2004-01-13 18:28:57 |
|
| [25] bbb | 2004-01-13 18:28:57 |
 Sziasztok!
Elsős egyetemista koromban analízis gyakorlaton azt bizonyítottuk, hogy az 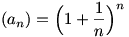 sorozat korlátos, pl. felső korlát a 3. A gyakorlatot vezető tanár úr szerint ennél pontosabb becslés nem is adható a felső korlátra elemi módszerekkel (tehát határértékszámítás használata nélkül). Felajánlotta, hogy ha ez valakinek mégis sikerülne, annak ad egy tábla csokoládét. Nekem sikerült, ám még mindig nem kaptam meg a megéremelt jutalmat. De mindez lényegtelen. A feladat a következő lenne: bbh sorozat korlátos, pl. felső korlát a 3. A gyakorlatot vezető tanár úr szerint ennél pontosabb becslés nem is adható a felső korlátra elemi módszerekkel (tehát határértékszámítás használata nélkül). Felajánlotta, hogy ha ez valakinek mégis sikerülne, annak ad egy tábla csokoládét. Nekem sikerült, ám még mindig nem kaptam meg a megéremelt jutalmat. De mindez lényegtelen. A feladat a következő lenne: bbh
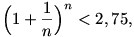
ahol n=1,2,.... A bizonyításhoz mellőzzétek a határértékszámításból tanultakat, mert így igazán izgalmas. Jó munkát!
|
|
| [24] Csizmadia Gábor | 2003-12-24 00:54:31 |
 Ugyan nem tudom, hogy ez kinek mennyire nehéz, de szerintem ezek a feladatok megérdemlik, hogy ide kerüljenek, leginkább a C. Az A és a B esetén nem csak konkrét példára gondolok, hanem egy kicsit általánosabb megoldásra.
10. feladat Konstruálj olyan valós-valós (R->R) függvényt (ha létezik ilyen), amely értelmezési tartományának minden nem megszámlálható részhalmazán felveszi a teljes értékkészletet. A. Az értékkészlet ekvivalens N-nel B. Az értékkészlet ekvivalens N-nel, valamint a függvény mindenütt differenciálható C. Az értékkészlet ekvivalens R-rel
|
|
|
|
| [21] Rácz Béla | 2003-12-16 21:52:54 |
 Egy igazi ínyencség, amit egyes érdekes ízlésű emberek diákolimpiára (1,5 óra/feladat) akartak kitűzni:
9. feladat
Mely (f, g) valósokon értelmezett valósértékű függvénypárokra teljesül minden x és y esetén az alábbi egyenlőség?
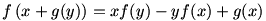
|
|
| [20] Pach Péter Pál | 2003-12-12 19:44:27 |
 Egy újabb feladat:
8. feladat
Legyen  >0. Keressük a legnagyobb >0. Keressük a legnagyobb  számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( - - )n különböző egész szám 1 és n között úgy, hogy a megadott számok közül egyik sem osztója egy másik kétszeresének. Adjuk meg 1 és n között a lehető legtöbb egész számot ezzel a tulajdonsággal. )n különböző egész szám 1 és n között úgy, hogy a megadott számok közül egyik sem osztója egy másik kétszeresének. Adjuk meg 1 és n között a lehető legtöbb egész számot ezzel a tulajdonsággal.
Megjegyzés:
Félreértések elkerülése végett:  -t nem -t nem  függvényében keressük. függvényében keressük.
|
|
|
| [18] nadorp | 2003-12-12 16:17:28 |
 Kedves Béla !
Most lehet,hogy égni fogok, de közlök egy megoldást a 6. feladatra. Nem tudom elhinni, hogy csak a triviális megoldás létezik ( azaz a sorozat elemei egyenlőek ), de a hibát nem találom. Szóval:
Legyen a p polinom n-ed fokú és írjunk fel egy Euklideszi algoritmushoz hasonlót
p(x)=(x-q2)p1(x)+q1
p1(x)=(x-q3)p2(x)+r2
p2(x)=(x-q4)p3(x)+r3
. . .
pn-2(x)=(x-qn)pn-1(x)+rn-1
Ebből következik, hogy a p polinom alkalmas s2,s3,...sn+1 racionális számokkal felírható a következő alakba:
p(x)=(x-q2)...(x-qn+1)sn+1+(x-q2)...(x-qn)sn+...(x-q2)s2+q1
A fenti eljáráshoz hasonlóan,"eggyel később kezdve",alkalmas t2,t3,...tn+1 számokkal
p(x)=(x-q3)...(x-qn+2)tn+1+(x-q3)...(x-qn+1)tn+...(x-q3)t2+q2
Írjunk a második egyenlőségben x helyére p(x)-et és használjuk fel egyrészt a qi számok közti összefüggést, másrészt, hogy minden polinomban p(x)-p(a)=(x-a)h(x) minden "a" számra. Kapjuk:
p(p(x))=(x-q2)...(x-qn+1)hn+1(x)+(x-q2)...(x-qn)hn(x)+...(x-q2)h2(x)+q1, ahol hi(x) alkalmas racionális együtthatós polinom. Az előzőek alapján
p(p(x))+p(x)=(x-q2)...(x-qn+1)(hn+1(x)+sn+1)+(x-q2)...(x-qn)(hn(x)+sn)+...(x-q2)(h2(x)+s2)+q1+q2
Ha most a fenti egynlőségben x=q3, akkor azt kapjuk, hogy
(q3-q2)(h2(x)+s2)=0
Mivel h2(x) legalább elsőfokú polinom, ez csak úgy lehet, hogy q2=q3.
Teljesen hasonló módszerrel kapjuk, hogy q3=q4 stb. Végül a q3=q2 összefüggésből p(q3)=p(q2), azaz q2=q1 következik.
|
| Előzmény: [16] Rácz Béla, 2003-12-11 00:30:39 |
|
| [17] Rácz Béla | 2003-12-11 19:42:01 |
 Eszembe jutott még egy darab. Nagyon örülnék neki, ha valaki elegáns megoldást adna rá, mert én csak elég kellemetlen bizonyításról tudok. A feladat egy háromszögben a beírt kör középpontjának az Euler-egyeneshez való viszonyát tisztázza:
7. feladat
A beírt kör K középpontjából a súlypontot és a magasságpontot összeköző SM szakasz több, mint 90°-ban látszik; más szóval K benne van az SM átmérőjű körben.
Sőt, ez az állítás éles: ha adottak az S,M,K pontok úgy, hogy ez a feltétel teljesüljön, akkor rajzolható hozzájuk megfelelő háromszög.
|
|
| [16] Rácz Béla | 2003-12-11 00:30:39 |
 Ez a magyar-izraeli versenyen volt pár éve:
6. feladat
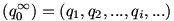 egy végtelen sorozat, ami racionális számokból áll; és p egy legalább másodfokú racionális együtthatós polinom. Tudjuk, hogy p(qi+1)=qi minden lehetséges i-re. egy végtelen sorozat, ami racionális számokból áll; és p egy legalább másodfokú racionális együtthatós polinom. Tudjuk, hogy p(qi+1)=qi minden lehetséges i-re.
Bizonyítandó, hogy a (q) sorozat periodikus.
|
|
| [15] Pach Péter Pál | 2003-12-08 20:40:47 |
 Kedves Péter!
A G gráf egy automorfizmusa: csúcsainak egy  permutációja, amelyre az i és j pontok közötti élek száma megegyezik a permutációja, amelyre az i és j pontok közötti élek száma megegyezik a  (i) és (i) és  (j) pontok közötti élek számával minden (i,j) párra. (j) pontok közötti élek számával minden (i,j) párra.
Részletezve: Megszámozzuk a gráf pontjait 1-től n-ig(, ha n pontja van). Tegyük fel, hogy ezután át tudjuk számozni a gráf pontjait úgy, hogy minden 1 i i j j n esetén teljesül, hogy ha az i. és j. pont között a „régi” számozás mellett futott él, akkor az „új” számozás mellett is fut és ha a „régi” számozás mellett nem futott él, akkor az „új” mellett sem fut. (Amennyiben a gráf nem egyszerű, akkor azt is megköveteljük, hogy ugyanannyi él fusson.) Az „új” számozást (vagyis a gráf pontjainak ezt a permutációját) a gráf egy automorfizmusának nevezzük. Minden gráfnak van legalább egy automorfizmusa: az identitás (amikor minden pont száma változatlan marad). (Általában egy „véletlenszerűen” felrajzolt gráfnak nincs is más automorfizmusa.) n esetén teljesül, hogy ha az i. és j. pont között a „régi” számozás mellett futott él, akkor az „új” számozás mellett is fut és ha a „régi” számozás mellett nem futott él, akkor az „új” mellett sem fut. (Amennyiben a gráf nem egyszerű, akkor azt is megköveteljük, hogy ugyanannyi él fusson.) Az „új” számozást (vagyis a gráf pontjainak ezt a permutációját) a gráf egy automorfizmusának nevezzük. Minden gráfnak van legalább egy automorfizmusa: az identitás (amikor minden pont száma változatlan marad). (Általában egy „véletlenszerűen” felrajzolt gráfnak nincs is más automorfizmusa.)
Példák:
- Az n pontú teljes gráfnak automorfizmusainak száma n!.
- Egy (2<)n hosszú kör automorfizmusainak száma 2n.
- A Petersen-gráf automorfizmusainak száma 120.
Az automorfizmusokat pedig úgy szorozhatjuk össze, hogy összeszorozzuk a hozzájuk tartozó permutációkat. Innen már végig lehet gondolni, hogy valóban csoportot alkotnak…
A példádat egyébként ismerem, úgyhogy Attilára, vagy másra vár a feladat, hogy megoldja, és feltegye a megoldást.
|
| Előzmény: [11] nadorp, 2003-12-08 13:53:55 |
|
| [14] Pach Péter Pál | 2003-12-08 20:29:51 |
 Térjünk vissza a 3. feladathoz, és a [4]-ben feltettem kérdésemhez. A kérdésre a válasz az, hogy nem, és nem csak „ehhez hasonlóan” nem bizonyítható, hanem egyáltalán nem, ugyanis nem is igaz.
A feladat átfogalmazható úgy, hogy 0<y1,y2,…,yn esetén igaz-e, hogy 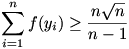 , ha , ha 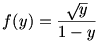 . .
Az f függvény a ![\left[0;\sqrt{\frac43}-1\right]](keplet.cgi?k=D8FAC312033F382D) intervallumon konkáv, a intervallumon konkáv, a 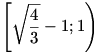 intervallumon pedig konvex. Ezt f’’(x) előjelének vizsgálatával (amihez másodfokú egyenletet kell megoldanunk) állapíthatjuk meg. intervallumon pedig konvex. Ezt f’’(x) előjelének vizsgálatával (amihez másodfokú egyenletet kell megoldanunk) állapíthatjuk meg.
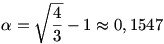
Ha n=3, akkor ha y1,y2,y3 mind legalább  , akkor készen vagyunk a Jensen-egyenlőtlenséggel. Ha közülük egy, vagy kettő , akkor készen vagyunk a Jensen-egyenlőtlenséggel. Ha közülük egy, vagy kettő  -nál kisebb, akkor a többi „annyira nagy” lesz, hogy még erősebb becslést nyerünk. (Ezt viszonylag gyorsan ki lehet hozni.) Viszont, ha n nagy, akkor lehetséges, hogy akár az összes yi kisebb, mint -nál kisebb, akkor a többi „annyira nagy” lesz, hogy még erősebb becslést nyerünk. (Ezt viszonylag gyorsan ki lehet hozni.) Viszont, ha n nagy, akkor lehetséges, hogy akár az összes yi kisebb, mint  , s ilyenkor éppen a Jensen-egyenlőtlenség mutatja, hogy , s ilyenkor éppen a Jensen-egyenlőtlenség mutatja, hogy 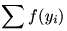 még csökkenthető. (Hiszen a [0; még csökkenthető. (Hiszen a [0; ] intervallumon f konkáv.) ] intervallumon f konkáv.)
|
| Előzmény: [4] Pach Péter Pál, 2003-12-02 23:05:43 |
|




 Z; Az I. és II. egyenlet alapján
Z; Az I. és II. egyenlet alapján 

 (n+1), ha n pozitív egész.
(n+1), ha n pozitív egész.  (n) a szám pozitív osztóinak összege, tehát
(n) a szám pozitív osztóinak összege, tehát 

 >0. Keressük a legnagyobb
>0. Keressük a legnagyobb  számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható (
számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( permutációja, amelyre az i és j pontok közötti élek száma megegyezik a
permutációja, amelyre az i és j pontok közötti élek száma megegyezik a  i
i