| [403] Cckek | 2006-10-16 14:56:14 |
 A következő egyszerünek tűnő problémához kéne egy kis segítség: Határozzuk meg 2n számjegyeinek a számát. Persze ezt lehet általánosítani de már ebben a formában is nagyon nehéznek tűnik.
|
|
|
|
| [400] qkac | 2006-10-15 21:56:22 |
 Így van megadva a feladat:
Milyen számot(betűt) írjunk az x helyébe, hogy az alábbi egyenlőségláncolatok igazak legyenek? (A hatványalapok mindegyike 1-től különböző pozitív valós szám) a) a3=b4=(ab)x b) p2=q3=(pq)2x
|
| Előzmény: [399] Lóczi Lajos, 2006-10-15 21:50:30 |
|
|
|
|
| [396] qkac | 2006-10-15 20:09:55 |
 Valaki nem tudja levezetni ezt a két példát? a) a3=b4=(ab)x b) p2=q3=(pq)2x Milyen számot(betűt) írjunk az x helyébe, hogy az alábbi egyenlőségláncolatok igazak legyenek?
|
|
|
|
|
| [392] Sirpi | 2006-10-04 09:16:59 |
 a) igen b) nem
Amúgy szerintem ha 1,4-szeresnek adod meg a sebességet, azzal túl sokat árulsz el, úgy nem annyira feltűnő, hogy min múlik a dolog, ha azt mondod, hogy Jerry 5m/s sebességgel tud úszni, a macskák pedig 7m/s sebességgel tudnak futni.
Mondjuk ekkor vagy Jerry úszik rekordsebességgel, vagy a macskák vannak nagyon ellustulva :-) Én amúgy úgy ismertem, hogy négyzet alakú karám, középen egy bárány, a 4 sarokban farkasok, és körben kerítés, de a bárány át tud bújni alatta, viszont a farkasok nem. Tudom, semmit nem változtat, csak gondoltam leírom :-)
Megoldást pedig egyelőre nem szeretnék közzétenni, remélem nem baj.
|
| Előzmény: [391] rizsesz, 2006-10-03 23:43:58 |
|
| [391] rizsesz | 2006-10-03 23:43:58 |
 Kedves Sirpi, még egyszer köszönöm. Tudom, nem ez a típus, de hátha: :)
Négyzet alakú medencében úszkál Jerry. Megjelenik 4 Tom :) a medence 4 sarkánál, akik macskák, így nem mennek a vízbe. A macskák 1,4 szer olyan gyorsan haladnak kint, mint Jerry a vízben. El tudja-e érni Jerry úgy a partot, hogy abban a pillanatban, amikor kiért, ott ne legyen macska? A macskák persze rendkívül intelligensek, semmi olyat nem tesznek, amit Jerry a maga javára tudna fordítani, képesek az egér mozgásától függő összehangolt stratégiát követni. Mindenki pontszerű. Állítás: Jerry kijuthat, kérdés, hogy hogyan? b., rész: A macskák 1,5-szor gyorsabbak. Kijuthat ilyenkor Jerry?
|
| Előzmény: [378] Sirpi, 2006-09-29 13:37:12 |
|
| [390] Cckek | 2006-10-03 21:22:26 |
 Dehogynem. Persze nem akarlak én kioktatni, de minél többet foglalkozol a matematikával, annál egyszerűbbnek fog tűnni. Úgyanakkor bonyólodik is, hisz egyre több kérdést teszel fel. De pont ez a szép benne...:)
|
| Előzmény: [388] Vini, 2006-10-03 21:08:00 |
|
|
|
|
|
| [385] Vini | 2006-10-03 18:33:52 |
 Sziasztok. Az alábbi feladattal akadtam el. Köszi előre is a segítséget.
Határozzuk meg a kifejezés értékét, ha 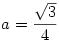
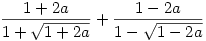
|
|
| [384] Sirpi | 2006-10-02 23:06:11 |
 Tegyük fel, hogy c 2, d 2, d 2. Ekkor (c-1)(d-1) 2. Ekkor (c-1)(d-1) 1, vagyis cd 1, vagyis cd c+d. Viszont a+b=cd c+d. Viszont a+b=cd c+d=ab, vagyis (a-1)(b-1) c+d=ab, vagyis (a-1)(b-1) 1, innen pedig következik, hogy a=1 vagy b=1, vagy mindkettő 2. Ha mindkettő 2-es, a másik kettő is az, ezt könnyű látni, tehát egy megoldás már van: a=b=c=d=2 1, innen pedig következik, hogy a=1 vagy b=1, vagy mindkettő 2. Ha mindkettő 2-es, a másik kettő is az, ezt könnyű látni, tehát egy megoldás már van: a=b=c=d=2
Innentől feltehető, hogy van a számok közt legalább egy 1-es. Legyen ez a. Ekkor viszont b+1=cd, b=c+d, ezekből cd-c-d=1, vagyis (c-1)(d-1)=2 Innen c és d értéke 2 és 3, vagyis megkaptuk a másik megoldást is: a=1, b=5, c=2, d=3.
|
| Előzmény: [382] rizsesz, 2006-10-02 22:35:53 |
|
| [383] rizsesz | 2006-10-02 22:38:11 |
 Ja az egyetlen megoldás, ami eddig szembe jött velem az (a;b)=(1;5), (c;d)=(2;3).
|
|
| [382] rizsesz | 2006-10-02 22:35:53 |
 Sziasztok! Van egy remek feladatom, amelyről nem tudom, hogy vannak-e már gondolkodások, de a google nem segített rajtam :( ez a következő egyenletrendszer lenne a pozitív egészek körében: a+b=c*d (1) a*b=c+d (2)
Ha bárkinek valami konstruktív ötlete támad, azt nagyon szívesen venném.
|
|
|
| [380] nadorp | 2006-10-02 11:43:22 |
 Szerintem a példa helyesen így van, a második tagot elírtad.
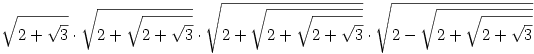 . .
Kezdjük el a végén a harmadik és negyedik taggal, és használjuk fel az (a-b)(a+b)=a2-b2 azonosságot.
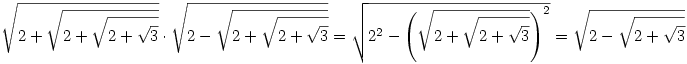
Most vegyük a második tagot és a fent kapott eredményt

Végül az első tagot és fenti utolsó eredményt véve
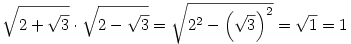
|
| Előzmény: [379] Vini, 2006-10-02 10:00:32 |
|
| [379] Vini | 2006-10-02 10:00:32 |
 Sziasztok. Tudna nekem segíteni valaki az alábbi feladat megoldásába? Előre is kösz. Számítsa ki a köv. kif. értékét:
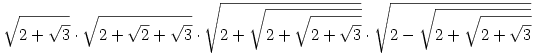
|
|







 2, d
2, d 1, innen pedig következik, hogy a=1 vagy b=1, vagy mindkettő 2. Ha mindkettő 2-es, a másik kettő is az, ezt könnyű látni, tehát egy megoldás már van: a=b=c=d=2
1, innen pedig következik, hogy a=1 vagy b=1, vagy mindkettő 2. Ha mindkettő 2-es, a másik kettő is az, ezt könnyű látni, tehát egy megoldás már van: a=b=c=d=2