| [473] thukaert | 2007-01-27 15:40:42 |
 Sziasztok!Volna 3 feladat amivel sehogy sem boldogulok, ha valaki tudna segíteni megköszönném
1.Határozzuk meg az n-edik primitív egységgyökök kettős szorzatainak az összegét!
2.Határozzuk meg azon egyenlet együtthatói közötti kapcsolatot, amelynek gyökei egy derékszögű háromszög szinuszaival egyenlők!
3.X,Y n-ed rendű négyzetes mátrixok.Bizonyítsuk be hogy
XY-YX = C megoldható X,Y -ban <=> C nyoma nulla
Előre is köszönöm mindenkinek
|
|
| [472] thukaert | 2007-01-27 14:52:09 |
 A problémára trigonometrikus megoldás is van, bár feleslegesnek tartom, hiszen egyszerűen az
(a+b)(a-b)=a*a-b*b
azonosságot kell felhasználni.
A másik megoldáshoz pedig használd fel a
cos(x/2)=sqrt[(1+cos(x))/2], sin(x/2)=sqrt[(1-cos(x))/2], sin(2x)=2sin(x)cos(x)
azonosságokat, ez szép bár felesleges.
|
| Előzmény: [379] Vini, 2006-10-02 10:00:32 |
|
|
|
|
| [468] Cckek | 2006-12-08 17:09:37 |
 Van-e végtelen sok prímszám, mely három egymásutáni prímszám összege? ilynek pl a 23=5+7+11 vagy a 31=7+11+13
Repetitio est mater studiorum:))
|
|
| [467] Tewu | 2006-12-07 21:19:28 |
 te valami nagyon okos ember lehetsz köszi szépen :D
|
|
| [466] rizsesz | 2006-12-07 21:17:59 |
 x+y=xy=x/y. a második kettőből y négyzete 1, tehát y=1 vagy -1. ha y = 1, akkor pl. az 1. 2 egyenletből x+1=x, ennek nincsen megoldása, ha pedig y=-1, akkor x-1=-x, x=0,5. az egyetlen megoldás a (0,5;-1), x és y szerepe felcserélhető.
|
|
| [465] Tewu | 2006-12-07 21:16:02 |
 Sziasztok! 2 szám összege, szorzata és hányadosa megeggyezik. Melyik ez a 2 szám? lécci lécci valaki segítsen még ma kéne :) köszii előre is jah és eggyenletben kéne felírni
|
|
|
|
|
| [461] ágica | 2006-12-02 13:12:07 |
 Ez egy lineáris diffegyenlet (azaz y'(x)-f(x)y(x)=g(x) alakú), amit úgy oldunk meg, hogy először megkeressük a homogén megoldásokat, azaz az y'(x)-f(x)y(x)=0 egyenlet megoldásait: 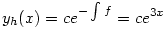 (c valós konstans). Aztán keresünk egy partikuláris megoldást a következő alakban: yp(x)=c(x)e3x (állandók variálásának módszere). Ezt behelyettesítve az eredeti egyenletbe kapjuk, hogy c'(x)=(2x)/(e3x), ahonnan c(x)=-(2+6x)/(9e3x), tehát yp(x)=-(2+6x)/9. Így a diffegyenlet megoldása: y(x) = yh(x)+yp(x) = ce3x-(2+6x)/9. (c valós konstans). Aztán keresünk egy partikuláris megoldást a következő alakban: yp(x)=c(x)e3x (állandók variálásának módszere). Ezt behelyettesítve az eredeti egyenletbe kapjuk, hogy c'(x)=(2x)/(e3x), ahonnan c(x)=-(2+6x)/(9e3x), tehát yp(x)=-(2+6x)/9. Így a diffegyenlet megoldása: y(x) = yh(x)+yp(x) = ce3x-(2+6x)/9.
|
| Előzmény: [460] ., 2006-12-02 11:15:20 |
|
| [460] . | 2006-12-02 11:15:20 |
 Hy All! Van itt valaki aki ért a z=f(y/x) típusú differenciálegyenletekhez?
Hogy kell megoldani az y'=2x+3y diffegyenletet? Előre is köszi
|
|
|
|
|
|
| [455] s.addam | 2006-11-26 11:12:08 |
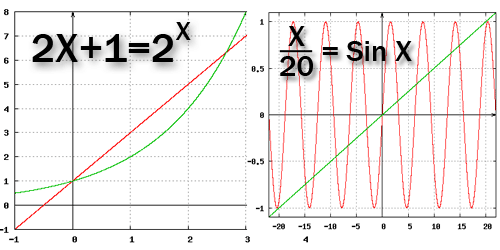
 Az alábbi két függvény összes gyöke csak grafikusan hetározható meg?
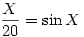
2X+1=2X
|
 |
|
| [454] Cckek | 2006-11-25 23:26:35 |
 Van-e végtelen sok prímszám, mely három egymásutáni prímszám összege? ilynek pl a 23=5+7+11 vagy a 31=7+11+13
|
|
| [453] nadorp | 2006-11-25 18:43:08 |
 Félreértés ne essék, a megoldás az említett Lovász László könyvben található és valóban nagyon szép. Az általad említett valószínűség k-tól való függetlensége ( az i értékétől nyilván nem függ) valóban meghökkentő, de igaz. Egyébként erre az 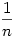 valószínűségre a könyvben van egy másik, rendkívül ötletes, számolás nélküli megoldás is. valószínűségre a könyvben van egy másik, rendkívül ötletes, számolás nélküli megoldás is.
|
| Előzmény: [452] rizsesz, 2006-11-25 17:50:44 |
|
| [452] rizsesz | 2006-11-25 17:50:44 |
 Kedves nadorp!
Nagyon szépen köszönöm, a megoldásod nagyon tetszik, bár egy pont elég furcsa, nevezetesen az, hogy hogy az i elem egy k hosszú körnek az eleme, na ennek a valószínűsége ugyanakkora minden i és k esetén :). üdv, András
|
|
| [451] nadorp | 2006-11-25 14:21:19 |
 Sziaszok !
Rizsesz elszámoltad. Annak a valószínűsége,hogy 1 kör lesz 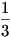 , két köré , két köré 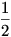 és három köré és három köré 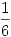 , tehát a várható érték , tehát a várható érték 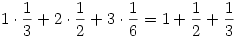 . Azért írtam így,mert n-re a várható érték . Azért írtam így,mert n-re a várható érték 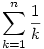 , ami nagy n-re tényleg ln n. Találtam erre egy szinte számolás nélküli - szerintem KÖNYVBE való - módszert Lovász László: Kombinatorikai feladatok és problémák című könyvében. ( hála Jenei Attilának, most már nekem is megvan ). Megpróbálom vázolni: , ami nagy n-re tényleg ln n. Találtam erre egy szinte számolás nélküli - szerintem KÖNYVBE való - módszert Lovász László: Kombinatorikai feladatok és problémák című könyvében. ( hála Jenei Attilának, most már nekem is megvan ). Megpróbálom vázolni:
Először határozzuk meg annak a valószínűségét, hogy az i elem egy k hosszú körnek az eleme. Ez nyilván úgy határozható meg, hogy az i mellé még 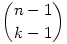 -féleképpen vehetünk k-1 számot, ezeknek (k-1)! sorrendje van, a maradék n-k elemnek pedig (n-k)! sorrendje van. A keresett valószínűség -féleképpen vehetünk k-1 számot, ezeknek (k-1)! sorrendje van, a maradék n-k elemnek pedig (n-k)! sorrendje van. A keresett valószínűség 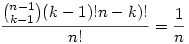 . .
Legyen most 1 k k n rögzített és definiáljuk az Xi valószínűségi változót a következőképpen: n rögzített és definiáljuk az Xi valószínűségi változót a következőképpen:
Xi=1 ha i eleme egy k hosszú körnek és legyen 0 különben. Nyilván X1+X2+...+Xn a k hosszú körökben levő elemek száma és 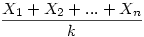 a k hosszú körök száma. Ezért a k hosszú körök számának várható értéke a k hosszú körök száma. Ezért a k hosszú körök számának várható értéke 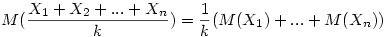 . Mivel . Mivel 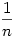 annak a valószínűsége, hogy i egy k hosszú körnek az eleme ezért annak a valószínűsége, hogy i egy k hosszú körnek az eleme ezért 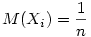 , azaz , azaz 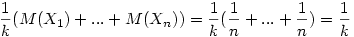 , azaz várhatóan , azaz várhatóan 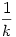 darab k hosszú kör lesz, így a körök számának várható értéke darab k hosszú kör lesz, így a körök számának várható értéke 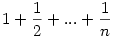 . .
|
| Előzmény: [450] Csimby, 2006-11-23 01:59:48 |
|
| [450] Csimby | 2006-11-23 01:59:48 |
 Bocsi! Csak nem tudom anélkül hogy lehetne megcsinálni, legalábbis nekünk ahhoz volt gyakorlófeladat. És ezért azt hittem ti is tanultátok és azért került elő nálatok is ez a feladat. Szóval akkor Jordan formula (egyesek szerint Jordán Károlytól, mások szerint Charles Jordan-tól származik :-)):
A1,A2,...,An tetsz. események. Jelölje N, hogy hány teljesül közülük. Ekkor 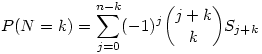
Ahol Sj-t már az előbb definiáltam. Jordan-formula speciális esete a Poincare avagy Szita-formula, Logikai-szita stb...
Mondjuk kezdessz elbizonytalanítani, szóval lehet hogy valamit elnézek vagy roszul emlékszem, ha ennyire más jön ki. Kéne írni rá egy programot ami megnézi nagyobb n-ekre is...
|
| Előzmény: [449] rizsesz, 2006-11-23 00:54:53 |
|
| [449] rizsesz | 2006-11-23 00:54:53 |
 lévén, közgazdász-hallgató a magamféle, nem tudom, hogy mi az a Jordan-formula. hiszek benne, hogy erre van valami emberi és kedves magyarázat. viszont, ahogy emlékszem, tovább is számoltuk, és lényegesen dinamikusabban nő a dolog, mint lne, legalábbis tudom, hogy tizen belül előfordult már 3-nál nagyobb szám is.
|
| Előzmény: [448] Csimby, 2006-11-22 23:43:01 |
|











 k
k