| [492] Cckek | 2007-02-07 10:22:42 |
 A következő tipusú integrálokat kéne kiszámítani:
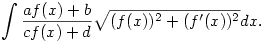
Ahol f(x) valamilyen trigonometrikus függvény a,b,c,d valós számok.
|
|
| [491] Gyöngyő | 2007-01-29 18:08:31 |
 Sziasztok!
Tudnátok segíteni az A.414 feladat megoldásában,mert elrontottam a végégt de nem tudom kijavítani.
Üdv.: Zsolt
|
|
|
| [489] nadorp | 2007-01-29 14:38:59 |
 Az 1.feladat vázlatosan.
Legyen 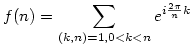 , ha n>1 és f(1)=1 , ha n>1 és f(1)=1
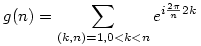 , ha n>1 és g(1)=1 , ha n>1 és g(1)=1
Nyilván f(n) az n-dik primítiv egységgyökök összege, g(n) pedig a négyzetösszege,ezért a kettős szorzatok összege 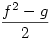 . Először bizonyítsuk be, hogy f és g multiplikatívok. Ha ez megvan, akkor kiszámolható, hogy . Először bizonyítsuk be, hogy f és g multiplikatívok. Ha ez megvan, akkor kiszámolható, hogy
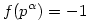 , ha , ha  =1 és 0 egyébként, azaz f(n)= =1 és 0 egyébként, azaz f(n)= (n) a Möbius-féle függvény. Hasonlóan kapjuk, hogy g(n)= (n) a Möbius-féle függvény. Hasonlóan kapjuk, hogy g(n)= (n), tehát a keresett összeg (n), tehát a keresett összeg 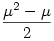 , ami 1, ha n prím és 0 különben. , ami 1, ha n prím és 0 különben.
|
| Előzmény: [473] thukaert, 2007-01-27 15:40:42 |
|
| [488] thukaert | 2007-01-27 22:31:53 |
 A,B legyen két egész elemű mátrix, és legyenek ezek relációban pontosan akkor ha létezik olyan U egész elemű unimoduláris mátrix amellyel A-t balról megszorozva B-t kapjuk.
1) Bizonyítsuk be hogy ekvivalenciarelációt kapunk! 2) Határozzuk meg a k determinánsú n-edrendű mátrixok ekvivalencia-osztályainak a számát!
|
|
| [487] Csimby | 2007-01-27 18:49:04 |
 Én ezt úgy ismerem, hogy egy amőba roszat álmodik és ösze-visza forgolódik/nyúlik stb álmában, de eközben sosem lóg le az ágyáról ami mondjuk kör vagy négyzet alakú. Bizonyítsuk be hogy lesz olyan pontja ami ugyanott ébred fel mint ahol lefeküdt.
Könnyebb a következő: Egy kígyó roszat álmodik és öszevisza tekeredik az alvócsövében, de nem lóg ki belőle. Biz be, hogy lesz olyan pontja ami ugyanott ébred mint ahol lefeküdt.
|
| Előzmény: [482] thukaert, 2007-01-27 18:00:16 |
|
|
|
| [484] thukaert | 2007-01-27 18:07:31 |
 Így gondolkoztam Lajos
Legyen a három gyök 1,x,y!Tegyük fel hogy a polinom normált!
Ekkor a másodfokú tag együtthatója:
-1-x-y
az első fokú tag együtthatója
x+y+xy
a konstans tag:
-xy
ha ezeket összeadod az -1 és nem gondoltunk a főegyütthatóra ami 1. -1+1=0
|
| Előzmény: [481] Lóczi Lajos, 2007-01-27 17:55:31 |
|
|
| [482] thukaert | 2007-01-27 18:00:16 |
 Íme egy aranyos feladat:
D:=[0,1]x[0,1]
f : D--->D folytonos
Mutassuk meg hogy f-nek van fixpontja!
Ja és Brouwer fixponttételét nem illik felhasználni!
|
|
|
|
|
|
| [477] thukaert | 2007-01-27 16:40:34 |
 Igen,egy harmadfokú polinomegyenletre gondoltam,olyan összefüggés kellene szerintem, amelyben az együtthatók szerepelnek,azok egész kitevős hatványai,és persze az alapműveletek.
|
| Előzmény: [474] Lóczi Lajos, 2007-01-27 15:51:48 |
|
|
|
|
| [473] thukaert | 2007-01-27 15:40:42 |
 Sziasztok!Volna 3 feladat amivel sehogy sem boldogulok, ha valaki tudna segíteni megköszönném
1.Határozzuk meg az n-edik primitív egységgyökök kettős szorzatainak az összegét!
2.Határozzuk meg azon egyenlet együtthatói közötti kapcsolatot, amelynek gyökei egy derékszögű háromszög szinuszaival egyenlők!
3.X,Y n-ed rendű négyzetes mátrixok.Bizonyítsuk be hogy
XY-YX = C megoldható X,Y -ban <=> C nyoma nulla
Előre is köszönöm mindenkinek
|
|
| [472] thukaert | 2007-01-27 14:52:09 |
 A problémára trigonometrikus megoldás is van, bár feleslegesnek tartom, hiszen egyszerűen az
(a+b)(a-b)=a*a-b*b
azonosságot kell felhasználni.
A másik megoldáshoz pedig használd fel a
cos(x/2)=sqrt[(1+cos(x))/2], sin(x/2)=sqrt[(1-cos(x))/2], sin(2x)=2sin(x)cos(x)
azonosságokat, ez szép bár felesleges.
|
| Előzmény: [379] Vini, 2006-10-02 10:00:32 |
|
|
|
|
| [468] Cckek | 2006-12-08 17:09:37 |
 Van-e végtelen sok prímszám, mely három egymásutáni prímszám összege? ilynek pl a 23=5+7+11 vagy a 31=7+11+13
Repetitio est mater studiorum:))
|
|





 =1 és 0 egyébként, azaz f(n)=
=1 és 0 egyébként, azaz f(n)= (n) a Möbius-féle függvény. Hasonlóan kapjuk, hogy g(n)=
(n) a Möbius-féle függvény. Hasonlóan kapjuk, hogy g(n)=


