| [517] epsilon | 2007-04-07 10:23:44 |
 Helló! Adott a következő négyzetes alak: F(x,y,z)=x(exp2)+axy+by(exp2)+z(exp2) és a kötés xyz=c ahol a,b,c,x,y,z>0. Kerestetik a minF=? Próbáltam a Lagrange módszerrel, ott nem találtam minimumhelyet. Tévedtem? Nincsen? Van egyszerűbb megoldás? Előre is kösz, üdv: epsilon
|
|
| [516] szbela | 2007-02-22 22:19:35 |
 nos átgondoltam mégegyszer, tényleg igazad van:) túl szépnek tűnt az ötletem...:) hogy elégtételt vegyek, feladok egy nagyon szép feladatot, Komáromban hallottam egy diáktalálkozón, már nem emlékszem, hogy kitől származik, íme: adott A=2x+y+2x+z+2y+z ahol x,y,z>0 valós számok. a megoldandó példa:
8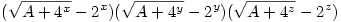 = =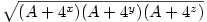 x=? y=? z=? x=? y=? z=?
jó éjszakát!
|
|
| [515] jenei.attila | 2007-02-22 20:12:15 |
 Az OK, hogy y2x+x2z+z2y+xyz 4xyz. De amit írtál: "Tehát ahol 4xyz-nek maximuma van, ott van y2x+x2z+z2y+xyz -nek a minimuma", nos ezt nem értem, és pont ezt kifogásoltam az előző hozzászolásomban.De az általad felírt egyenlőtlenségekből: (x+y)(x+z)(y+z)<=8/27 és y2x+x2z+z2y+xyz 4xyz. De amit írtál: "Tehát ahol 4xyz-nek maximuma van, ott van y2x+x2z+z2y+xyz -nek a minimuma", nos ezt nem értem, és pont ezt kifogásoltam az előző hozzászolásomban.De az általad felírt egyenlőtlenségekből: (x+y)(x+z)(y+z)<=8/27 és y2x+x2z+z2y+xyz 4xyz csak az következik, hogy 4xyz csak az következik, hogy 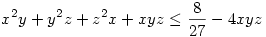 , ebből pedig, ahogy írtam, csak akkor következik az eredeti egyenlőtlenség, ha , ebből pedig, ahogy írtam, csak akkor következik az eredeti egyenlőtlenség, ha 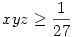 , ez pedig éppen fordítva áll. Egyébként nem állítottam, hogy a 8/27-4xyz maximumát kerested. , ez pedig éppen fordítva áll. Egyébként nem állítottam, hogy a 8/27-4xyz maximumát kerested.
|
| Előzmény: [513] szbela, 2007-02-22 18:51:58 |
|
|
| [513] szbela | 2007-02-22 18:51:58 |
 nekem ez jónak tűnik... átgondoltam még egyszer, és számomra még mindig úgy tűnik, hogy igazam van, mégpedig azért, mert amit mondasz jó, de nem 8/27-4xyz maximumát, hanem a y2x+x2z+z2y+xyz kifejezésnek a minimumát keresem, és ez a kifejezés mindig nagyobb, mint 4xyz. Tehát ahol 4xyz-nek maximuma van, ott van y2x+x2z+z2y+xyz -nek a minimuma, és minél kisebb ez, annál nagyobb az (x+y)(x+z)(y+z)-(y2x+x2z+z2y+xyz), vagyis az eredeti baloldal.
|
|
| [512] PPP | 2007-02-22 18:27:55 |
 Én is teszek egy kísérletet :-)
Ha xyz=0, akkor pl. z=0 esetén számtani-mértanival 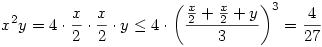
Egyenlőség akkor van, ha 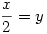 , azaz ha x=2/3, y=1/3. , azaz ha x=2/3, y=1/3.
Tegyük fel most, hogy xyz 0. Legyen x, y és z közül nagyságrendben a középső mondjuk y. (x,y,z) hármas helyett (x+z,y,0) hármasra áttérve a kifejezés értéke (x+z)2y-x2y-y2z-z2x-xyz=z2y+xyz-y2z-z2x=z(y-x)(z-y) 0. Legyen x, y és z közül nagyságrendben a középső mondjuk y. (x,y,z) hármas helyett (x+z,y,0) hármasra áttérve a kifejezés értéke (x+z)2y-x2y-y2z-z2x-xyz=z2y+xyz-y2z-z2x=z(y-x)(z-y) 0-val nő. A kifejezés értéke eredetileg 4/27-nél kisebb volt, ha ez pozitív, vagy ha (x+z,y,0)-ra nem áll egyenlőség. Ha (x+z,y,0)-ra a kifejezés értéke pont 4/27, akkor x+z=2/3, y=1/3. z(y-x)(z-y)=0, ezért - mivel z nemnulla - x=y vagy z=y. Mindkét esetben az x=y=z=1/3 megoldást kapjuk. 0-val nő. A kifejezés értéke eredetileg 4/27-nél kisebb volt, ha ez pozitív, vagy ha (x+z,y,0)-ra nem áll egyenlőség. Ha (x+z,y,0)-ra a kifejezés értéke pont 4/27, akkor x+z=2/3, y=1/3. z(y-x)(z-y)=0, ezért - mivel z nemnulla - x=y vagy z=y. Mindkét esetben az x=y=z=1/3 megoldást kapjuk.
|
| Előzmény: [505] Sümegi Károly, 2007-02-21 18:00:44 |
|
| [511] szbela | 2007-02-22 18:25:00 |
 helló Attila! igazad van, köszi szépen. ez esetben gondolkodom még rajta...:)
|
|
|
| [509] szbela | 2007-02-22 16:54:46 |
 sziasztok! nekem is hasonló megoldásom lenne, íme: írjuk fel a baloldalt a következőképp: (x+y)(x+z)(y+z)-(y2x+x2z+z2y+xyz) innen a geometriai és a számtani közép között fennálló összefüggésből megtudjuk határozni (x+y)(x+z)(y+z) maximumát, ami (2/3)3, azaz 8/27. Ez x=y=z esetében áll fenn. Most határozzuk meg y2x+x2z+z2y+xyz kifejezés minimumát a számtani közép és a geometriai közép segítségével, ami 4xyz, és akkor áll fenn, ha x=y=z. És ehhez kell, hogy meghatározzuk xyz maximumát, amit szintén a már sokszor használt számtani és mértani középpel tudunk megtenni. így 4xyz értéke (1/3)3*4, azaz 4/27. Kifejezésünk maximuma tehát nem más, mint 8/27-4/27, azaz 4/27, ami az előzőekből következve x=y=z=1/3 esetben áll fenn. Utólagos elnézést a sok szöveghez, most először használtam a TeX-et.
|
|
|
|
|
| [505] Sümegi Károly | 2007-02-21 18:00:44 |
 Köszönöm a megoldást, a módszert ismertem. Nem tudom van-e elemibb megoldása. A feladat nehézségét az adja, hogy a megszokott egyenlőtlenségekkel nehezen bizonyítható, mert több helyen is felveszi a szélsőértékét. Egy hétig próbálkoztam vele, de nem sikerült. Ha valaki megoldaná deriválás nélkül, az érdekelne. A feladat felsőbb matematikával történő megoldása eléggé jól működik.
|
| Előzmény: [504] Lóczi Lajos, 2007-02-20 14:28:40 |
|
| [504] Lóczi Lajos | 2007-02-20 14:28:40 |
 Aki szereti az ilyen tipusu feladatokat, azoknak ajanlom figyelmebe a www.artofproblemsolving.com oldal forumanak tanulmanyozasat: naponta tobb tucat ilyen feladatot tuznek ki.
A mostani feladat megintcsak nem lesz nehez, ha tudunk derivalni. Legyen f(x,y) az egyenlotlenseg bal oldala a z=1-x-y helyettesites utan. Megmutatjuk, hogy f abszolut maximuma 4/27 az x=0, y=0, x+y=1 egyenesek altal hatarolt haromszoglapon, amibol a feladat mar kovetkezik.
A parcialis derivaltakat 0-val egyenlove teve a haromszog belsejeben 4 lehetseges szelsoertekhely adodik: (1/3,1/3), illetve egy harmadfoku egyenlet harom gyokenel, amit most nem masolok ide. Itt f(1/3,1/3)=4/27, a maradek harom pontban pedig f erteke 1/7, ami kisebb 4/27-nel.
Hatra van a perem vizsgalata. Kulon nezve az f(0,y), f(x,0) es f(x,1-x) egyvaltozos fuggvenyeket megallapitjuk, hogy ezek legfeljebb 4/27-et vesznek fel, megpedig csak az alabbi helyeken: (0,2/3), (1/3,0), (2/3,1/3), amivel befejezodik az erveles.
|
| Előzmény: [499] Sümegi Károly, 2007-02-19 14:35:14 |
|
|
| [502] jonas | 2007-02-19 20:37:00 |
 Én így kezdeném el:
Vezessük be az f(t)=tp-1(1-t)n jelölést. Ezzel az integrált így írhatjuk.
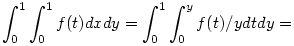
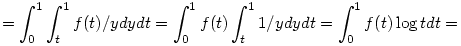
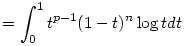
(Ha p 1, akkor esetleg lehetnek gondok az integrál felcserélésével.) 1, akkor esetleg lehetnek gondok az integrál felcserélésével.)
Innen viszont nem tudom, hogy mennék tovább.
|
| Előzmény: [496] Cckek, 2007-02-18 19:29:46 |
|
| [501] nadorp | 2007-02-19 14:53:22 |
 ... és a kígyó a saját farkába harap -:). Olyan "nagyon szép" alakot szerintem azért ne nagyon várjál, mert az integrálban a Gamma-függvény van elrejtve.
|
| Előzmény: [500] Cckek, 2007-02-19 14:43:27 |
|
|
| [499] Sümegi Károly | 2007-02-19 14:35:14 |
 Van egy nehéz feladatom:
x,y,z nemnegatív számokra x+y+z=1.
Bizonyítsuk be, hogy 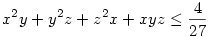
|
|
| [498] nadorp | 2007-02-19 11:26:09 |
 Így van, nekem is ez jött ki a binomiális tételből. De találtam egy "szebb" ( bár ez hozzáállás kérdése -:) alakot. Tehát
![\sum_{k=0}^n \binom{n}{k} \frac{(-1)^k}{(p+k)^2}=-n!\left[\frac1{p(p+1)(p+2)...(p+n)}\right]^'](keplet.cgi?k=289AD7F48DF267C1) ( természetesen p-szerinti deriváltról van szó) ( természetesen p-szerinti deriváltról van szó)
|
| Előzmény: [497] Lóczi Lajos, 2007-02-19 11:10:01 |
|
|
|
|
|
| [493] Lóczi Lajos | 2007-02-07 12:26:39 |
 Amit ki lehet egyáltalán számolni, arra nézve lásd http://integrals.wolfram.com/
(Gyakran segít, ha paraméterek helyett konkrét számokkal dolgozol -- a paramétereket komplex számokként kezeli alaphelyzetben, melyek néha bonyolult esetszétválasztásokat eredményeznek.)
|
| Előzmény: [492] Cckek, 2007-02-07 10:22:42 |
|



 4xyz. De amit írtál: "Tehát ahol 4xyz-nek maximuma van, ott van y2x+x2z+z2y+xyz -nek a minimuma", nos ezt nem értem, és pont ezt kifogásoltam az előző hozzászolásomban.De az általad felírt egyenlőtlenségekből: (x+y)(x+z)(y+z)<=8/27 és y2x+x2z+z2y+xyz
4xyz. De amit írtál: "Tehát ahol 4xyz-nek maximuma van, ott van y2x+x2z+z2y+xyz -nek a minimuma", nos ezt nem értem, és pont ezt kifogásoltam az előző hozzászolásomban.De az általad felírt egyenlőtlenségekből: (x+y)(x+z)(y+z)<=8/27 és y2x+x2z+z2y+xyz 0. Legyen x, y és z közül nagyságrendben a középső mondjuk y. (x,y,z) hármas helyett (x+z,y,0) hármasra áttérve a kifejezés értéke (x+z)2y-x2y-y2z-z2x-xyz=z2y+xyz-y2z-z2x=z(y-x)(z-y)
0. Legyen x, y és z közül nagyságrendben a középső mondjuk y. (x,y,z) hármas helyett (x+z,y,0) hármasra áttérve a kifejezés értéke (x+z)2y-x2y-y2z-z2x-xyz=z2y+xyz-y2z-z2x=z(y-x)(z-y) xyz lenne, ami éppen fordítva áll fenn. Mindkettőtöknél az a hiba, hogy egy egyenlőtelnségben (ahol a baloldal <= mint a jobboldal), nem biztos, hogy akkor lesz a baloldal maximális, ha a jobboldal minimális (mégha ilyenkor egyenlők is).
xyz lenne, ami éppen fordítva áll fenn. Mindkettőtöknél az a hiba, hogy egy egyenlőtelnségben (ahol a baloldal <= mint a jobboldal), nem biztos, hogy akkor lesz a baloldal maximális, ha a jobboldal minimális (mégha ilyenkor egyenlők is).




 R,n
R,n