|
| [541] amynna | 2007-06-09 19:34:13 |
 Én is most vettem észre, hogy 1/b feladatot tényleg elnézted, mert én minuszt irtam. sehogy nem jött ki a nekem az eredmény. megpróbálom mégegyszer felrakni, nagyon örülnék, ha tudnátok segiteni és nemcsak az eredményt irnátok le, hanem a levezetést is. Nagyon köszönöm. Franciska
|
| Előzmény: [540] Sirpi, 2007-06-09 11:55:35 |
|
| [540] Sirpi | 2007-06-09 11:55:35 |
 Igen, a gyökös feladatot elnéztem, kétszer is: egyrészt rosszul olvastam el a feladatot, másrészt a meg a rossz feladatra is elírtam a megoldást, köszi a helyreigazítást :-)
|
| Előzmény: [538] Fálesz Mihály, 2007-06-09 06:35:21 |
|
| [539] Fálesz Mihály | 2007-06-09 06:42:14 |
 Az azért mindig relatív, hogy milyen problémák a nehezebbek...
| ... Erre apukám megint elmondta, hogy őt nem érdekli, hogy más gyereke mit csinál, de nagyon szégyellte magát helyettem a tanító néni előtt. Sajnáltam apukámat, hogy helyettem szégyellte magát, mert szégyellni már én is tudom magamat a tanító néni előtt, csak szép kövér karikákat nem tudok még egyedül rajzolni. (Janikovszky Éva: Velem mindig történik valami) |
|
|
| Előzmény: [537] Sirpi, 2007-06-09 00:34:36 |
|
|
| [537] Sirpi | 2007-06-09 00:34:36 |
 Zárójel-fóbiád van? :-) Csak mert nem tettél ki egyet sem, pedig látható, hogy rengeteg helyre kellett volna. És ez eléggé egy (nem is túl nehéz) gyakorló feladatsornak tűnik, gondolom nem sok haszna lenne, ha tálcán kapnád az összes megoldást, ezért első körben tényleg inkább csak rávezetést adnék, ahogy írtad is az egyik hsz-edben korábban (kivéve a deriválós példáknál, ott egyszerűen nem tudtam a végeredmény leírása nélkül segíteni - ott próbáld meg Te is kiszámolni a deriváltat és vesd össze a két eredményt)
1a) emelj ki az 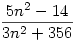 törtből n2/n2-et, és ekkor már elég könnyű látni, hogy a megmaradó tört hova tart. törtből n2/n2-et, és ekkor már elég könnyű látni, hogy a megmaradó tört hova tart.
1b) emeljünk ki a 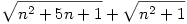 kifejezésből kifejezésből 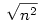 -et, és használjuk ki, hogy n2+5n+1=(n+5/2)2-21/4. -et, és használjuk ki, hogy n2+5n+1=(n+5/2)2-21/4.
2a) f'(x)=20x3-x-1/2-6.x-3
2b) f'(x)=3x2cos x-x3sin x
2c) gondolom itt az 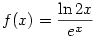 fv.-ről van, szó (bár a leírás nem könnyíti meg a helyzetem), ez esetben f'(x)=(1/x-ln 2x).e-x fv.-ről van, szó (bár a leírás nem könnyíti meg a helyzetem), ez esetben f'(x)=(1/x-ln 2x).e-x
3) 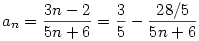 . Ebből nyilvánvaló, hogy a sorozat korlátos (hiszen monoton növekszik), és határértéke 3/5. . Ebből nyilvánvaló, hogy a sorozat korlátos (hiszen monoton növekszik), és határértéke 3/5.
4) f páros, ha f(x)=f(-x), páratlan, ha f(x)=-f(-x) minden x-re. A beírt (helyesen f(x)=x2/(1+x2)) függvény két páros függvény hányadosa, tehát páros.
Amúgy ezek a feladatok sokkal inkább az ujjgyakorlatok, mintsem a nehezebb matematikai problémák tárgykörébe tartoznak...
|
| Előzmény: [536] amynna, 2007-06-08 17:35:28 |
|
| [536] amynna | 2007-06-08 17:35:28 |
 ime: 1.) Számitsuk ki a sorozatok határértékét:
a./ an= 5n2-14n/3n2+356n b./ an= gyökjeln2+5n+1-gyökjeln2+1
2.) deriválni kell a függvényeket. a.) f(x)= 5x4-2gyökjelx +3/x2 b.) f(x)= x3. cosx c.) f(x)= ln2x/ex
3.) be kell bizonyitani a sorozat korlátosságát, monitását
an= 3n-2/ 5n+6
4.) Mikor mondjuk, egy függvényről, hogy páros ill.páratlan? paritás vizsgálat: f(x)=x2/1+x2
|
|
|
|
| [533] nadorp | 2007-06-08 13:59:10 |
 1. F(x)=3x3-2x2+5x-1
F'(x)=9x2-4x+5
F''(x)=18x-4
Ott lehet szélsőérték,ahol F'(x)=0. Mivel a másodfokú egyenlet diszkriminánsa negatív és F'(x) főállású parabola, ezért F'(x)>0, tehát F(x) szigorúan monoton növekvő.
2. f(x)=xln x
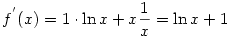 felhasználtuk, hogy (fg)'=f'g+fg' felhasználtuk, hogy (fg)'=f'g+fg'
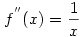
Ott lehet szélsőérték, ahol f'(x)=ln x+1=0, tehát 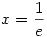 . .
Ha 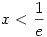 , akkor f'(x)<0, a függvény csökken , akkor f'(x)<0, a függvény csökken
Ha 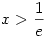 , akkor f'(x)>0, a függvény nő , akkor f'(x)>0, a függvény nő
A fentiekből következik, hogy 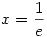 -ben minimum van -ben minimum van
3.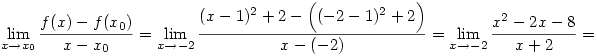
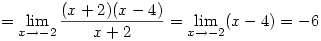
|
| Előzmény: [531] amynna, 2007-06-08 12:37:21 |
|
| [532] amynna | 2007-06-08 13:03:02 |
 Hú nagyon fontos, hogy valaki rávezessen..::!!!
|
|
| [531] amynna | 2007-06-08 12:37:21 |
 Na akkor mégegyszer, egy kis segitség kellene anal.ból...
A függvényen el kell végezni a monotonitás és szélsőérték vizsgálatot és meg kell adni a függvény második deriváltját is. F(x)=3x3-2x2+5x-1 sajna nem tudom helyesen jelölni a függvényt, de ezt ti értitek, hogy a harmadikon, másodikon... ez is kellene , f(x)=xlnx
másik példa: a differenciálhányados definiciójára épitve ki kellen számitani az f(x)=(x-1)2+2 függvény xo/null/=-2 helyen vett differenciálhányadosát.
|
|
| [530] amynna | 2007-06-08 12:35:56 |
 Segitsen ki valaki, hogyan kell itt hozzászólni eltűnt a szövegem is.? Franci
|
|
|
|
| [527] Lóczi Lajos | 2007-05-23 17:22:57 |
 Adjunk példát olyan f 0 függvényre (ha egyáltalán van), hogy 0 függvényre (ha egyáltalán van), hogy
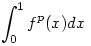
minden p>1 szám esetén végtelen, de p=1 esetén véges.
|
|
| [526] Doom | 2007-05-19 14:46:32 |

Ekkor (1)-ből kifejezve x-et:
és ezt behelyettesítve (2)-be kapjuk, hogy
64-4y-6z+y+3z=31
33=3y+3z
11=y+z
Ezt visszahelyettesítve (4)-be:
x=32-2y-33+3y
(5)-öt és (6)-ot beírva (3)-ba:
3y-3+2y+11-y=28
4y=20
y=5
Így visszahelyettesítve kapjuk, hogy x=4, y=5 és z=6.
Megjegyzés: ez mindenféle meggondolás nélkül, "favágó" módszerrel csináltuk és minden lineáris egyenletrendszer esetében működik.
|
| Előzmény: [525] Csill, 2007-05-19 12:24:25 |
|
| [525] Csill | 2007-05-19 12:24:25 |
 Nagy bajban vagyok. Szeretném megtudni, hogy hogyan lehet megoldani ezt a feledatot, hogy az eredmény (x, y, z):(4, 5, 6)legyen? A feladat: x+2y+3z = 32 (és) 2x+y+3z = 31 (és) 3x+2y+z = 28. Segítség!!!!!
|
|
| [524] Lóczi Lajos | 2007-04-08 00:33:18 |
 Valaki a Lagrange-féle multiplikátor módszerrel kereste meg az x-y4-z4 függvény szélsőértékeit az x3+y2+z2=0 feltétel mellett. Mit tapasztalt és mi ennek az oka?
|
|
|
| [522] epsilon | 2007-04-07 20:24:15 |
 Helló! Köszi a gyors véleményeket, javaslatokat! Én azért hagytam benne a kötést is, mert akkor az L(x,y,z)=x(exp2)+axy+by(exp2)+z(exp2)+K(xyz-36) esetén a deriváltak nem olyan kellemetlenek mint a 2 változósra visszavezetett esetén, de nekem itt a 3 parciális derivátnál az adódott, hogy egyidőben nem lehet x,y,z mind pozitív :-( pedig ez kellene, mert aztán a kötésbe vissza kellene írnom. Megnézem még a 2 változós esetet is, de azért elemi megoldásra is gondolnék, az a=b=4 setben, bosszantóan egszerűnek látszik az az eset, de nekem is 3-ik és négyzetgyökök jöttek ki :-( gondoltam, hogy valami jópofább számokra találok. Üdv: epsilon
|
|
| [521] Lóczi Lajos | 2007-04-07 20:08:20 |
 Persze az egészhez nem is kell multiplikátor-módszer, hiszen a feltételi egyenletből z kifejezhető x-szel, y-nal és c-vel: egy feltétel nélküli kétváltozós probléma marad a pozitív síknegyedben, minimalizálandó az 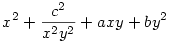 függvény. (A megfelelő parciális deriváltakból álló egyenletrendszer megoldása természetesen így sem lesz könnyebb és ugyanarra az eredményre vezet.) Ebből az alakból viszont látszik, hogy pontosan egy globális minimum lesz. függvény. (A megfelelő parciális deriváltakból álló egyenletrendszer megoldása természetesen így sem lesz könnyebb és ugyanarra az eredményre vezet.) Ebből az alakból viszont látszik, hogy pontosan egy globális minimum lesz.
|
| Előzmény: [520] Lóczi Lajos, 2007-04-07 19:57:34 |
|
| [520] Lóczi Lajos | 2007-04-07 19:57:34 |
 A Lagrange-függvény stacionárius pontja (=ahol a deriváltjának minden komponense nulla) nem fejezhető ki szép képlettel: egy olyan harmadfokú egyenlet szerepel benne, amelynek együtthatói egy másodfokú egyenlet gyökeinek hatodik gyöke, mindenesetre ebből egyetlen lehetséges szélsőértékhely adódik.
Egy konkrét példát kiragadva: az a=1, b=2, c=4 esetben a lehetséges szélsőértékhely:
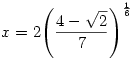 , , 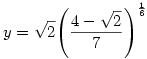 , , 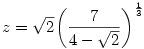 . .
Erről egyébként a másodikderivált-kritériummal be lehet látni, hogy feltételes minimum.
|
| Előzmény: [517] epsilon, 2007-04-07 10:23:44 |
|
|
| [518] nadorp | 2007-04-07 16:31:04 |
 Ugye ez a feladat: x2+axy+by2+z2 minimuma az xyz=c feltétel mellett? Ha igen, akkor ne keress minimumot. Legyen x=y=n pozitív egész és 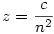 . Ekkor F(x,y,z)=(1+a+b)n2+z2 és ez tetszőleges nagy lehet. . Ekkor F(x,y,z)=(1+a+b)n2+z2 és ez tetszőleges nagy lehet.
|
| Előzmény: [517] epsilon, 2007-04-07 10:23:44 |
|






 L1 de f
L1 de f Lp,p>1? Bizonyára. De konkrétan kapni ilyet? Hmm:)
Lp,p>1? Bizonyára. De konkrétan kapni ilyet? Hmm:)
 0 függvényre (ha egyáltalán van), hogy
0 függvényre (ha egyáltalán van), hogy 