|
|
|
| [614] Róbert Gida | 2008-05-13 09:53:04 |
 De nulla. Az érdekes az, hogy a bizonyításához, hogy rossz csak az egyik híres Ramanujan kongurencia kell, eszerint: numbpart(5*k+4) 0 mod 5, így numbpart(11269)=...851 0 mod 5, így numbpart(11269)=...851 1 mod 5 nem lehet. 1 mod 5 nem lehet.
Külföldi levelezős fórumon téma. Ez az első rossz particiós szám, de 20000-es indexig még több, mint 10 ilyen van. Ahogy olvatstam a Maple 11-ben is hiba ez. De egy másik programban az ingyenes Pari-Gp-ben is rossz volt sokáig, de ott az első ellenpélda numbpart(52602)-re volt.
Nagy indexre a Rademacher formulával számolják a particiós számot a Pari-ban, nyilván a Mapleben is. Meglepő, hogy mennyire könnyű ezek szerint elrontani a programozását.
|
| Előzmény: [613] Lóczi Lajos, 2008-05-13 08:43:01 |
|
|
| [612] Róbert Gida | 2008-05-13 00:54:57 |
 Listaáron Magyarországon 800,000 forintért is árult Maple 9.5 szerint a 11269. partició szám a következő (,az alábbi utasításokkal tudjuk kiprintelni):
with(combinat);
numbpart(11269);
231139177231303975514411787649455628959060199360109972557851519105155176180318215891795874905318274163248033071851
Elhiggyem neki?
|
|
|
| [610] Róbert Gida | 2008-03-17 01:41:42 |
 Mondjuk az integrált nem tekinteném zártnak. Próbálgatással és Stirling-gel én ezt találtam, bizonyítani nem tudom, hogy ez egy korrekt közelítés, de n=106-ig a legnagyobb hibát n=1-re adja, ott a hiba kisebb, mint 1 ezred.
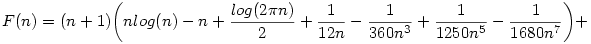
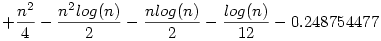
De nagyon valószínű, hogy n>1200-ra a hiba már kisebb, mint 10-9 mindig. A konstans is érdekes, az ismert inverz szimbólikus konstans kereső sem tud róla.
|
| Előzmény: [606] Lóczi Lajos, 2008-03-16 19:45:07 |
|
|
|
|
|
| [605] Róbert Gida | 2008-03-16 12:15:57 |
 Találjunk olyan zárt formulát, amely 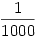 -nél kisebb hibával adja meg az alábbi összeget minden pozitív egész n-re: -nél kisebb hibával adja meg az alábbi összeget minden pozitív egész n-re:
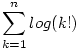
|
|
| [604] rizsesz | 2008-02-05 09:48:28 |
 A legkönnyebb a 3-asával tagolás megoldása - az egyesektől visszabontjuk 3-as blokkokra, és váltakozó előjellel összeadogatjuk őket; pl. 71435 esetében -71+435=364, osztható 7-tel, és az eredeti szám is. ez annak a következménye, hogy 7 1001-nek osztója.
|
|
| [603] jonas | 2008-02-05 09:36:40 |
 Nem könnyebb alkalmazni, de könnyebb megjegyezni azt a szabályt, hogy a 10a+b szám osztható 7-tel akkor és csak akkor, ha a-2b osztható 7-tel.
|
| Előzmény: [602] Csimby, 2008-02-05 02:55:01 |
|
| [602] Csimby | 2008-02-05 02:55:01 |
 Ha már itt tartunk, van "szabály" 7-re, sőt minden másra is. 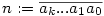 , ekkor n pontosan akkor osztható 7-tel, hogyha (a0+3a1+2a2+6a3+4a4+5a5)+(a6+3a7+2a8+... kifejezés osztható 7-tel. Ugye ez ugyanolyan típusú szabály mint pl. a 3-mal, 9-cel vagy 11-gyel való oszthatóságé, csak egy bonyolultabb sorozatot (1,3,2,6,4,5) kell hozzá megjegyezni. , ekkor n pontosan akkor osztható 7-tel, hogyha (a0+3a1+2a2+6a3+4a4+5a5)+(a6+3a7+2a8+... kifejezés osztható 7-tel. Ugye ez ugyanolyan típusú szabály mint pl. a 3-mal, 9-cel vagy 11-gyel való oszthatóságé, csak egy bonyolultabb sorozatot (1,3,2,6,4,5) kell hozzá megjegyezni.
Hogy ez miért működik? Azért mert:
100 1 (mod 7) 1 (mod 7)
101 3 (mod 7) 3 (mod 7)
102 2 (mod 7) 2 (mod 7)
103 6 (mod 7) 6 (mod 7)
104 4 (mod 7) 4 (mod 7)
105 5 (mod 7) 5 (mod 7)
106 1 (mod 7) és innentől ismétlődik a sorozat. 1 (mod 7) és innentől ismétlődik a sorozat.
|
| Előzmény: [601] sizeref, 2008-02-03 20:24:33 |
|
| [601] sizeref | 2008-02-03 20:24:33 |
 Mint irtam nem ezen a pályán vagyok ez nekem hobbi.De pl. 12 jegyű számrol 10-12 sec alatt eldöntöm,hogy osztható e 7-tel vagy sem.Nekem nem a gyorsaság volt a kérdés hanem az, hogy nincs rá szabály,legalább is ezt tanultam.Nekem az nem tetszett. Szóval van pl 3,4,5,6,8,9,11 re van szabály de a 7 kimaradt.Először csak a 7-tel való oszthatóság kérdése foglalkoztatott de aztán rájöttem, hogy minden prímszámra felírható az algoritmusom.Tehát mindenre van megoldás csak keresni kell.Egyenlőre tartozkodom az algoritmus kiírására.
|
|
| [600] Róbert Gida | 2008-01-18 20:53:16 |
 p=2-re megnézném az utolsó bitjét, ez O(1) költség a számítógépeken. Ha 0<abs(n)<p, akkor megint triviális a válasz. Továbbá, ha n "nem túl nagy" p-hez képest, akkor tényleg van gyorsabb ismert módszer is, mint a triviális, hogy osztok p-vel és megnézem a maradékot, ez implementálva van a gmp matematikai könyvtárban is, persze nemcsak prímekre működik ez. Ha n sokkal nagyobb, mint p, akkor szerintem nincs gyorsabb módszer, mint a hagyományos, nem is hiszek benne, hogy lenne, így elsőre. De, ha leírod a módszered, akkor meggyőzhetsz.
|
| Előzmény: [599] sizeref, 2008-01-18 18:28:30 |
|
| [599] sizeref | 2008-01-18 18:28:30 |
 Sziasztok! Nekem nincs problémám csak van megoldásom.A prímszámokkal való oszthatóságra van két algoritmusom mely eldönti egy adott számról,hogy osztható-e maradék nélkül vagy sem az adott szám pl.7-el.Matematikai biztonyítás is megvan rá,de mivel nem ezen a pályán vagyok nehéz kibontakoznom.Gyakorlatilag minden prímszámra felírható az algoritmus és az egyik az osztási eredményt is megadja anélkül, hogy az adott számot osztanám el az osztóval.Érdekel valakit?
|
|
|
|
| [596] Lóczi Lajos | 2007-12-13 20:11:52 |
 Az analízisből ismert, hogy egy függvény folytonossági, illetve szakadási pontjainak halmaza milyen típusú halmaz lehet, l. pl.
http://www.cs.elte.hu/ karatson/funkanal.pdf
Itt a C. 21-es Következmény bizonyítását nézd meg.
A bizonyítás egyszerű, de több, elemi előkészítő lépést igényel.
|
| Előzmény: [595] Gyöngyő, 2007-12-13 16:21:08 |
|
| [595] Gyöngyő | 2007-12-13 16:21:08 |
 Sziasztok!
Elírtam a feladatot.Pontosan így szó: Mutassuk meg,hogy nincs olyan függvény,amelyik irracionális pontokban nem folytonos,racionális pontokban folytonos.
Ez hasonló a Riemann-függvényhez,csak ott pont fordítva van.
Üdv.: Zsolt
|
|
|
|




 0 mod 5, így numbpart(11269)=...851
0 mod 5, így numbpart(11269)=...851
 '(-1)=-0.165421143700...
'(-1)=-0.165421143700...




 0 és itt a függvény folytonos, akkor bármely
0 és itt a függvény folytonos, akkor bármely  (>0) -hoz megadható olyan
(>0) -hoz megadható olyan  (>0) , hogy ha |x-q0|<
(>0) , hogy ha |x-q0|<
