| [630] Sirpi | 2008-05-25 07:54:18 |
 Már csak akkor látod mások (nem rejtett) mailcímét, ha be vagy jelentkezve, így ez már nem indok. Géza pedig sokra megy az infóval, hogy máshol megtalál, mert a regisztrációid nincsenek összekapcsolva.
Továbbra sem értem, hogy miért van szükséged erre a hozzáállásra, folyton támadsz, minősíthetetlen hangnemben tálalod a véleményed (pl. egy szó kimarad egy példából és máris "ultragagyi"-kat és hasonlókat pufogtatsz), de rád nem tehet megjegyzést senki. Legközelebb már nem fogom a fórumot zavarni, hogy megint szólok (vannak ennél érdekesebb témák is), helyette lesz egy kis időd gondolkodni (ha észrevételed van, akár a - publikus - mailcímemet is használhatod).
Ha mindenki szembejön Veled az autópályán, akkor nem biztos, hogy ők tévesztették el a sávot.
|
| Előzmény: [629] Róbert Gida, 2008-05-24 23:05:46 |
|
| [629] Róbert Gida | 2008-05-24 23:05:46 |
 A bankszámlaszámom/jelszavam nem kell? A regisztrációnál nincs is odaírva, hogy az eredeti nevünket használjuk. Egyébként én speciel nem is gondoltam rá, kb. 10 fórumon vagyok fent, van olyan, ahol névvel, fotóval, emailcímmel együtt, ahol kb. minden 10-edik ember adta meg a valódi nevét. Úgyhogy nem kell leordítani.
Spamek miatt sem publikus az emailcímem,az adatlapra kattintva kiírja ugyanis azt.
|
| Előzmény: [628] BohnerGéza, 2008-05-24 21:57:01 |
|
|
| [627] Róbert Gida | 2008-05-24 20:51:52 |
 Ez egyébként baromi ismert példa. Most néztem, a Konkrét Matematika című könyvben 6.43-as példa.
De a Mathematica programban a help menüben példaként is szerepel. Bár kipróbálva kb. 10 másodperc mire kiszámolja. Pedig 2 mértani sor összegeként felírva a példa triviális.
|
| Előzmény: [626] jonas, 2008-05-24 16:07:31 |
|
|
|
| [623] huber | 2008-05-24 13:51:21 |
 Ákos!
Köszönöm a segítséget!
huber
|
|
|
| [620] huber | 2008-05-24 13:12:25 |
 Üdv! Új vagyok és tapasztalatlan. Tudna valaki nekem segíteni? Egy végtelen sor összege vár rám: szumma fn/(10 az n+1. hatványon). A sor specialitása, hogy a számláló a Fibonacci sorozat elemeit tartalmazza, bár lehet, hogy csak az egész számokat? talán értem a feladatot, nem tudom...
Kérek segítséget!
huber
|
|
| [619] jonas | 2008-05-24 12:19:13 |
 Rondán néz ki a felírása, de szerintem ha átírod komplex összeggé, akkor a mértani sorokat összegezni lehet. Remélem, jól gondolom.
|
| Előzmény: [618] PAL, 2008-05-23 21:20:18 |
|
| [618] PAL | 2008-05-23 21:20:18 |
 Sziasztok!
Nem tudom, jó témához írom-e kérdésem, de számomra az egyik gyakorlaton kapott alábbi 2 állítás bizonyítása sajnos túlságosan is nehéznek bizonyult, aki tud kérem segítsen. Előre is köszönöm.
|
 |
|
|
|
|
| [614] Róbert Gida | 2008-05-13 09:53:04 |
 De nulla. Az érdekes az, hogy a bizonyításához, hogy rossz csak az egyik híres Ramanujan kongurencia kell, eszerint: numbpart(5*k+4) 0 mod 5, így numbpart(11269)=...851 0 mod 5, így numbpart(11269)=...851 1 mod 5 nem lehet. 1 mod 5 nem lehet.
Külföldi levelezős fórumon téma. Ez az első rossz particiós szám, de 20000-es indexig még több, mint 10 ilyen van. Ahogy olvatstam a Maple 11-ben is hiba ez. De egy másik programban az ingyenes Pari-Gp-ben is rossz volt sokáig, de ott az első ellenpélda numbpart(52602)-re volt.
Nagy indexre a Rademacher formulával számolják a particiós számot a Pari-ban, nyilván a Mapleben is. Meglepő, hogy mennyire könnyű ezek szerint elrontani a programozását.
|
| Előzmény: [613] Lóczi Lajos, 2008-05-13 08:43:01 |
|
|
| [612] Róbert Gida | 2008-05-13 00:54:57 |
 Listaáron Magyarországon 800,000 forintért is árult Maple 9.5 szerint a 11269. partició szám a következő (,az alábbi utasításokkal tudjuk kiprintelni):
with(combinat);
numbpart(11269);
231139177231303975514411787649455628959060199360109972557851519105155176180318215891795874905318274163248033071851
Elhiggyem neki?
|
|
|
| [610] Róbert Gida | 2008-03-17 01:41:42 |
 Mondjuk az integrált nem tekinteném zártnak. Próbálgatással és Stirling-gel én ezt találtam, bizonyítani nem tudom, hogy ez egy korrekt közelítés, de n=106-ig a legnagyobb hibát n=1-re adja, ott a hiba kisebb, mint 1 ezred.
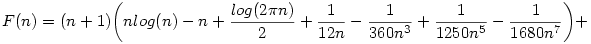
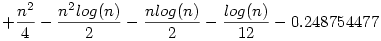
De nagyon valószínű, hogy n>1200-ra a hiba már kisebb, mint 10-9 mindig. A konstans is érdekes, az ismert inverz szimbólikus konstans kereső sem tud róla.
|
| Előzmény: [606] Lóczi Lajos, 2008-03-16 19:45:07 |
|
|
|
|
|
| [605] Róbert Gida | 2008-03-16 12:15:57 |
 Találjunk olyan zárt formulát, amely 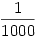 -nél kisebb hibával adja meg az alábbi összeget minden pozitív egész n-re: -nél kisebb hibával adja meg az alábbi összeget minden pozitív egész n-re:
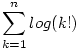
|
|
| [604] rizsesz | 2008-02-05 09:48:28 |
 A legkönnyebb a 3-asával tagolás megoldása - az egyesektől visszabontjuk 3-as blokkokra, és váltakozó előjellel összeadogatjuk őket; pl. 71435 esetében -71+435=364, osztható 7-tel, és az eredeti szám is. ez annak a következménye, hogy 7 1001-nek osztója.
|
|










 0 mod 5, így numbpart(11269)=...851
0 mod 5, így numbpart(11269)=...851
 '(-1)=-0.165421143700...
'(-1)=-0.165421143700...