|
| [62] Csimby | 2004-02-03 00:14:51 |
 Üdv!
Akik a parkettázós feladattal foglalkoznak (adott négyzetbe hány egységnyi kisnégyzet fér?) azoknak szeretnék néhány király címet mondani:
http://www.stetson.edu/ efriedma/squinsqu/
http://mathworld.wolfram.com/SquarePacking.html
|
|
| [61] pataki | 2004-02-01 06:54:00 |
 Kedves László, örülök, hogy a kérdés felkeltette az érdeklôdést (bár a "bárányok még hallgatnak", ami lehet reménykeltô is) én már egy ideje gondolkodom rajta. Mint a kitüzésembôl is kiderült,és igy remélem,hogy fair a játék, nem ismerek megoldást 5 szomszédos négyzetszám értékre.
Nem ismerek olyan eredményt sem, ami egyáltalán korlátot adna, hogy hány szomszédos helyen vehet föl négyzetszámot egy ilyen polinom, sôt, azt sem tudom, hogy van-e ilyen korlát. Úgy értem, minden n-hez lehet olyan polinom, ami n szomszédos helyen négyzetszám. (Az itt nem érdekes, hogy a dolog a nulláról indul, mert az elsôfokú tag együtthatója páros és igy el lehet tolni.) Szóval innen is lehetne támadni.
Van ugyan némi ködös kontextus, amiben az 5-nek van értelme, de teljesen homályos. Azért nem irom le, amit tudok, mert az befolyásolhatna másokat és itt fontos a friss fej, persze lehet, hogy nincs igazam. Másfelôl lényegében nem sokat tudok. Mindenesetre ha van megoldás, akkor az jó nagy. És akkor persze jönne a 6.
Ehhez a diofantikus megközelítéshez annyit, hogy ha nem építi be az ember a nemnulla diszkrimináns feltételt, akkor le kell kezelni a végtelen sok triviális megoldást. A te k-d egyébként jó jelzôszám, mert a diszkrimináns negyede. No ennyi. Üdvözlettel Pataki János
|
| Előzmény: [60] lorantfy, 2004-01-31 21:58:38 |
|
| [60] lorantfy | 2004-01-31 21:58:38 |
 Kedves Fórumosok!
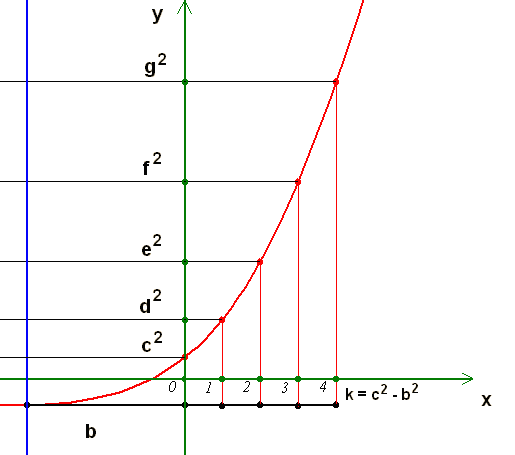
Apró ötlet a négyzetszámos polinomos példához. Hátha valaki kihoz belőle valamit, mert nekem sajnos most nincs időm rá: x2+Bx+C a másodfokú polinomunk. Eddig beláttuk, hogy B páros, így legyen B=2b és C=c2, hogy x=0-nál négyzetszám legyen az értéke.
Legyen k=b2-c2.
x2+2b+c2=(b+x)2-b2+c2=(b+x)2-(b2-c2)=(b+x)2-k
Az x=0,1,2,3,4 helyen felvett értékek: c2,d2,e2,f2,g2
c2=b2–k
d2=(b+1)2–k
e2=(b+2)2–k
f2=(b+3)2–k
g2=(b+4)2–k
5 egymás után következő egész szám négyzetéből kivonva ugyanazt a k egész számot újra négyzetszámokat kell kapnunk!
A négyzetszámok utolsó számjegye csak 0,1,4,5,6,9 lehet. A 0,1,2,3,4,5,6,7,8,9 utolsó számjegyekhez a 0,1,4,9,6,5,6,9,4,1 négyzetszám végződések tartoznak. Ezekből 5 egymásutánit (ciklikusan) kiválasztva és levonva belőle k utolsó számjegyét csak akkor kaphatunk mind az ötnél négyzetszám végződést, ha k szám 0-ra vagy 5-re végződik.
Tehát 5| k. Az egymás utáni 5 szám közül (b, b+1, b+2, b+3, b+4) egy biztos osztható 5-tel, vagyis négyzete osztható 25-tel. Ekkor viszont a bal oldalon álló megfelelő négyzetszám is oszható 5-tel, tehát 25-tel is. Így k két 25-tel osztható négyzetszám különbsége: 25| k.
Ha belátnánk még, hogy k páros, (vagy esetleg 4-el osztható), akkor a végén 0 (vagy két 0) áll. Így c, d, e, f, g számok négyzeteinek utolsó számjegye (vagy utolsó 2 számjegye) sorra egyenlő b, b+1, b+2, b+3, b+4 négyzeteinek utolsó jegyeivel. Ebből talán ellentmondásra lehetne jutni.
|
 |
| Előzmény: [56] Gubbubu, 2004-01-27 00:33:01 |
|
| [59] Gubbubu | 2004-01-27 20:20:55 |
 Elnézést - mielőtt bárki belém kötne - az "iletve" szót véletlenül (billentyűzetergonómiai gondok miatt) írtam egy l-lel! Helyesen: "illetve".
Üdv 1:00 körül: G.
|
| Előzmény: [58] Gubbubu, 2004-01-27 19:05:15 |
|
| [58] Gubbubu | 2004-01-27 19:05:15 |
 Kedves Kós Géza!
"4|B" nem egy állítás volt, hanem - ezek szerint nem egészen igaz - sejtés, ami - természeténél fogva - nem megindokolva, hanem inkább kérdezve van (iletve volt)! Nem csoda, ha nem érted, mivel ami nincs, az kicsit nehezebben érthető, mint ami van!
Üdv:G.
|
| Előzmény: [57] Kós Géza, 2004-01-27 16:32:35 |
|
| [57] Kós Géza | 2004-01-27 16:32:35 |
 A 4-gyel oszthatóság indoklását nem értem.
Az ilyen sejtéseket mindig érdemes tesztelni az olyan triviális megoldásokon, mint például x2+2x+1=(x+1)2. Ez a példa is mutatja, hogy a diszkrimináns vizsgálata nélkül nem jöhet ki, hogy a b a 2-n kívül bármivel is osztható.
|
| Előzmény: [56] Gubbubu, 2004-01-27 00:33:01 |
|
| [56] Gubbubu | 2004-01-27 00:33:01 |
 Kedves Algebristák!
A négyzetszám értékű polinommal annyira sikerült előrejutnom, hogy sikerült igazolnom Zormac immár klasszikus eredményeit, miszerint a konstans tag négyzetszám, és az elsőfokú tag együtthatója páros. Ezeket most gyorsan és röviden belátom. A feltétel miatt p(0) négyzetszám, c2=02+0.x+C, azaz C=c2. Azaz p(x)=x2+Bx+c2. Ekkor a négyzetszámértékűségi feltételek a következőket jelentik:
I. 1+B+c2=n12;
II. 4+2B+c2=n22;
III. 9+3B+c2=n32;
IV. 16+4B+c2=n42;
Ám a II. egyenletből 2B+c2 n22 (4). n22 (4).
x y (m) fogja jelölni, hogy x és y m-mel osztva azonos maradékot ad, azaz a mod(m) kongruenciát, a továbbiakban mindig mod(4) lesz a kongruencia, így nem írom ki a modulust). y (m) fogja jelölni, hogy x és y m-mel osztva azonos maradékot ad, azaz a mod(m) kongruenciát, a továbbiakban mindig mod(4) lesz a kongruencia, így nem írom ki a modulust).
És mivel B 0,1,2,3 esetén rendre 2B 0,1,2,3 esetén rendre 2B 0,2,0,2, ehhez a mod(4) 0-val vagy 1-gyel kongruens c2 számot adva rendre 0,2,0,2-t vagy 1,3,1,3-t adva a kapott szám (n22) is négyzetszám, vagyis mod(4) 0 vagy 1, amiből látható, hogy az első esetben (ha c2 0 modd(4)) is a 0,2,0,2 esetekből csak a 0-s esetek jöhetnek szóba, vagyis ha B 0 vagy 2 mod(4), azaz páros, és ugyanez van, ha az 1,3,1,3 lehetőséget nézzük (azaz ha c2 1 mod(4)). 0,2,0,2, ehhez a mod(4) 0-val vagy 1-gyel kongruens c2 számot adva rendre 0,2,0,2-t vagy 1,3,1,3-t adva a kapott szám (n22) is négyzetszám, vagyis mod(4) 0 vagy 1, amiből látható, hogy az első esetben (ha c2 0 modd(4)) is a 0,2,0,2 esetekből csak a 0-s esetek jöhetnek szóba, vagyis ha B 0 vagy 2 mod(4), azaz páros, és ugyanez van, ha az 1,3,1,3 lehetőséget nézzük (azaz ha c2 1 mod(4)).
Tehát B páros, így a B=2b jelöléssel írható p(x)=x2+2b+c2.
Megjegyzés: Figyeljük meg, hogy itt felhasználtuk, hogy a konstans tag négyzetszám.
Azt állítom, innen elindulva mod(8) be lehet látni, hogy b is páros, azaz B 4-gyel is osztható. Örülnék, ha mások is megerősítenének ebben.
Újra felírva a négyzetszámértékűségi feltételeket:
I. 1+2b+c2=n12;
II. 4+4b+c2=n22;
III. 9+6b+c2=n32;
IV. 16+8b+c2=n42;
I.-IV. alapján az is látható, hogy c2,n22,n42 kongruens mod(2), míg c2+1,n12,n32 is kongruens mod(2), és e két osztály elemei persze inkongruensek. Persze ugyanez mondható el e négyzetszámok "gyökeire" is.
Hát egyelőre csak ennyi... nem olyan sok... de még nem adtam fel...
Üdv mindenkinek:G.
|
|
| [55] Gubbubu | 2004-01-26 19:20:34 |
 Kedves Onogur!
A "közvetítői szerepemmel" kapcsolatos pozitív vagy (remélem, nem) negatív eredmény vagy e hét csütörtök, vagy jövő hét hétfő, de legkésőbb február 9. után egy-két nappal várható. Addig tehát biztosan nyugodtan "sütögethetitek" Lászlóval a kérdéses "négyzetzsúfolási" bizonyítást.
A másik úton, az interneten más d. geometriai tétel kapcsán már végeztem elég hosszadalmas kereséseket úgy egy fél éve, minden eredmény nélkül (még angol nyelvű cikkivonatokat vagy lényeges utalásokat sem találtam, nemhogy magyar nyelvű vagy rajzzal illusztrált cikkeket). Most majd megpróbálom néhány újabb keresőszóval (pl. Voronoi, Erdős-Graham, Graham stb.). A d. geometria nagyon fiatal (alig száz éves) tudományág, úgy tudom, még tankönyve sincs, tehát ez az eredménytelenség csak közepes mértékben meglepő.
Üdv. G.
|
| Előzmény: [50] Hajba Károly, 2004-01-26 00:01:18 |
|
| [54] lorantfy | 2004-01-26 15:58:57 |
 Kedves Károly!
Én is arra gondolok hogy egyre növekvő, persze nagyon kicsi elfordítások és apró eltolások vezetnek majd a megoldáshoz. Nyilván az a cél, hogy a külső üres sávból lefoglalt területeket befelé illetve "összetereljük". A belső négyzetek között is lesznek apró rések, de ezek összege kisebb lesz mint a kívül lefoglalt terület. Sorozatocskákat kell majd összegezni!
|
| Előzmény: [53] Hajba Károly, 2004-01-26 13:40:37 |
|
| [53] Hajba Károly | 2004-01-26 13:40:37 |
 Kedves László!
Örülök, hogy sikerült felpiszkálni az érdeklődésedet a téma iránt. Így már nem vagyok egyedül. :o) Én már vagy két éve vissza-visszatérek e témához alkalmanként, ...de hát nem én vagyok a PRÍM.
Arra már rájöttem, hogy 45°-os elfordítással csak akkor lehet alkalmas méret esetén megoldást találni, ha 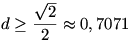 Pl.: 999.996,78 méret esetén 133.584 az elforgatott lapocskák esetén a többlet. De hát a d itt majd' 8-szoros. Továbbá kisebb méretek esetén vagy 0°-os vagy 45°-os elforgatott elemek esetén lehet 'jó' kitöltést találni. A köztes szögek a tapasztalatom szerint rontják a lehetőséget. Pl.: 999.996,78 méret esetén 133.584 az elforgatott lapocskák esetén a többlet. De hát a d itt majd' 8-szoros. Továbbá kisebb méretek esetén vagy 0°-os vagy 45°-os elforgatott elemek esetén lehet 'jó' kitöltést találni. A köztes szögek a tapasztalatom szerint rontják a lehetőséget.
Gyanítom, hogy a megoldásban minden elem egy kicsit jobban el van fordítva, de hát ezt legalább 3200-as méret esetén már számomra követhetetlen, kis méret esetén pedig még nem csökken a helyigényük.
Mindentől függetlenül Sirpi által vázolni próbált és általunk továbbgondolt eset is vezethet sikerre. Ki tudja?
Aki tudja szóljon!
HK
|
| Előzmény: [52] lorantfy, 2004-01-26 08:50:23 |
|
| [52] lorantfy | 2004-01-26 08:50:23 |
 Kedves Károly!
Sikerült rendesen felpiszkálnod az érdeklődésemet a téma iránt. Az az érzésem, hogy az eredeti megoldás megértéséhez is fel kell kötni a gatyánkat!
Gondolom a könyv szerzője is azért egyszerűsítette ilyen talányosan a műveletet: "ügyesen elcsúsztatva őket egymás mellett"-re, mert nem lehet pár mondattal egyszerűen megadni az eljárást.
Én arra gondoltam az előző megoldási kisérletemben, hogy az 1 fokos elforgatás után az oszlopok eltolásával a sarkokat CD vonalra lehet hozni és igy alul is illeszkedni fognak a négyzetek sarkai.
Csakhogy ezután ugyanezt keresztirányban már nem lehet megtenni.
|
| Előzmény: [51] Hajba Károly, 2004-01-26 01:13:06 |
|
| [51] Hajba Károly | 2004-01-26 01:13:06 |
 Kedves László!
Ha jól sejtem a CM vonal mentén közel 500.000 darab parkettát érint a belemetszés és az MF mentén egyáltalán nem vagy nagyon-nagyon keveset lehetne még többletként beillszteni. Ehhez képest a végén csak kb. 10 %-nyi új hely keletkezik. S ez nem sokat változik a szög mértékének módosításával sem.
A pontosabb itélethozatalhoz képleteket kellene felállítani  függvényében. függvényében.
De kiváncsi vagyok a Te észrevételedre is.
HK
|
| Előzmény: [49] lorantfy, 2004-01-24 10:28:59 |
|
| [50] Hajba Károly | 2004-01-26 00:01:18 |
 Kedves gubbubu!
Van egy sanda gyanúm, hogy a probléma nehezebben fog megoldódni, mint első ránézésre tűnik. Ezért közvetítői szereped nem felesleges, mit előre is köszönök.
Tehát "...1975-ben, a kombinatorikával foglalkozók legnagyobb meglepetésére és örömére Erdősnek és Grahamnek mégis sikerült nem 1, de több mint 100 ezer újabbat rakni a kezdeti 1 billió parkettához, ügyesen elcsúsztatva őket egymás mellett. Graham szerint az 1.000.000.100.000 parkettás megoldással közel jutottak az optimálishoz, a két matematikus mégsem tudta bebizonyítani, hogy ezzel a módszerrel lehet a leghatékonyabban kis négyzetekkel nagy négyzeteket lefedni. Két évtized múlt el, de az ő eljárásuk még mindig nem tudták jobbal felváltani. Nincs elégtétel, ha túl könnyű a tétel."
Azóta már lassan 30 év is eltelt, továbbá a fenti idézet előtt a könyv azt írja, hogy szabálytalan idomok esetén nem találnak hatékony stratégiát ill. a matematikai szakirodalom nem foglalkozik e (szabálytalan idomú lefedés) problémával. E témában a hálón bármilyen rajzzal illusztrált irodalom érdekel, ha fel tudsz ilyent kutatni.
HK
|
| Előzmény: [47] Gubbubu, 2004-01-23 18:27:29 |
|
| [49] lorantfy | 2004-01-24 10:28:59 |
 Kiegészítés az előzőhöz:
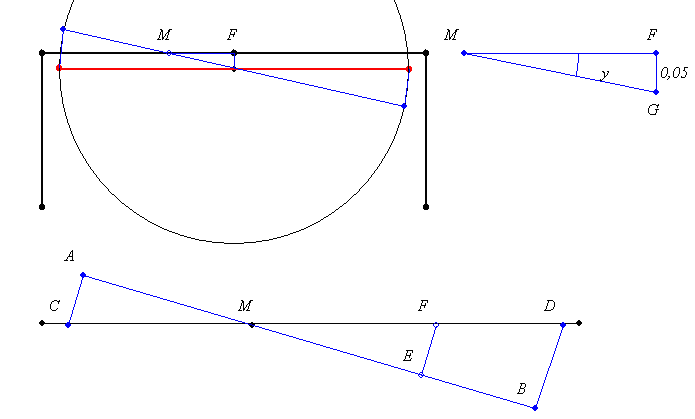
1 fokos elforgatás esetén y = MG = 2.86 és AM = 500000-y, BM = 500000+y.
AC = 8727,48, BD = 8727,58, EB= 2y = 5,73. Így az EBDF trapéz területe = 5x8727= 43635 parketta.
De, hogy ne örüljünk nagyon – Laci fiam felhívta a figyelmemet arra az aprócska problémára, ami a parkettadarabok diszkrét méretéből adódik. A kilógó ACM háromszögnél az összes olyan parkettadarabot ki kell venni amibe a CM egyenes belevág és ezeket persze nem lehet EFM háromszönél behelyezni a keretbe. De erre is van megoldás. Gondolkodjatok rajta!
|
 |
| Előzmény: [48] lorantfy, 2004-01-23 23:41:41 |
|
| [48] lorantfy | 2004-01-23 23:41:41 |
 Kedves Sirpi, Károly és Fórumosok!
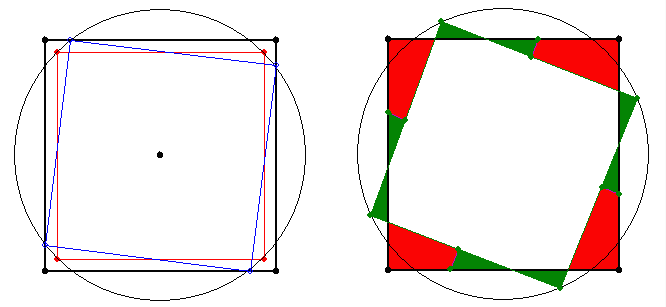
Azt hiszem nem elég a parkettákból álló négyzetet a keretnégyzet széléig fordítani, (mert az így kapott háromszögekbe még nem férnek bele a parketta négyzetek), hanem túl kell forgatni a kereten ! (Szóval jópárat ki kell szednünk és áthelyezni, ahhoz, hogy többet rakhassunk bele.)
A kilógó háromszögekben lévő kiskockákat áthelyezhetjük a szoszédos nagyobb háromszögekbe és még marad hely.
Nem számoltam utánna az adott méretekre, mert már félálomból jöttem vissza a gép elé, hogy ezt beírjam.
Remélem volt értelme. (Mármint, hogy jól gondolom.)
|
 |
| Előzmény: [45] Sirpi, 2004-01-23 14:33:08 |
|
| [47] Gubbubu | 2004-01-23 18:27:29 |
 Kedves Onogur!
Első olvasatra ez egy diszkrét geometriai, parkettázásokkal rokon probléma. Van egy ötletem, esetleg kinél érdeklődjek ez ügyben, ugyanis a jövő héten egy más ügyben beszélnem kell vele (csak egyáltalán nem tudom, mikor van bent pontosan, egyébként Böröczky Tanár Úrról van szó az ELTÉN), esetleg irodalmat vagy valami részletes útbaigazítást legalábbis tud adni, amit, ha sikerül, megpróbálok közvetíteni. Nem tudnád még megnézni a "Prímemberben", pontosan hogy hívták azokat, akik foglalkoztak-e problémával, esetleg jelent-e meg cikk róla, mi a címe, stb. (sajnos épp nincs nálam a könyv)? Persze ha megoldódna közben a problémád, értesíts, hogy ne érdeklődjek hiába.
Üdvözöl: G.
|
| Előzmény: [44] Hajba Károly, 2004-01-23 12:44:43 |
|
| [46] Hajba Károly | 2004-01-23 16:11:03 |
 Kedves Sirpi!
Lehet, hogy valamit félreértettem, de nekem a háromszög rövidebb oldalára csak az eltérés értéke jött ki, így ebbe még nem lehet belerakni semmit. Kérlek pontosítsd a magyarázatodat.
Köszi: HK
|
| Előzmény: [45] Sirpi, 2004-01-23 14:33:08 |
|
| [45] Sirpi | 2004-01-23 14:33:08 |
 Ki tud erről valamit? Röviden válaszolva: például én.
Amúgy pedig nem ördöngösség a dolog: tegyük a nagy négyzet alakú terem közepére a rengeteg parkettát koncentrikusan, szép szabályos négyzetrácsban. Ekkor mind a 4 oldalon lesz egy nagyon vékony rés (bocs, minjárt megyek haza, nincs idöm ábrát rajzolni, de szerintem követhetö a dolog). Most pedig egyszerüen forgassuk el a parketta-négyzetet annyira, hogy a csúcsai hozzáérjenek a terem oldalaihoz. Ekkor a 4 sarok mentén lesz 1-1 elnyújtott derkékaszögü háromszög, és mindbe bele lehet jópár négyzetet tenni. Akit érdekel, számolja ki, hogy mennyit. Remélem, tudtam segíteni.
S
|
| Előzmény: [44] Hajba Károly, 2004-01-23 12:44:43 |
|
| [44] Hajba Károly | 2004-01-23 12:44:43 |
 Kedves gubbubu!
Megemlítetted a PRÍM embert, s ezzel kapcsolatban lenne egy "igen nehéz" kérdésem. A róla szóló könyvben szerepel egy általa felvetett és megoldott feladat abból a műfajból, mely engem is érdekel, de a megoldásra egyáltalán nem utaltak.
Íme a feladata: Van egy 1.000.000,1 x 1.000.000,1 cm2 területű terem és le van fedve 1012 1x1 cm2-es parkettával. Megpróbáltak a maradák kis területre még néhányat elhelyezni és még 100.000 darabkát sikerült elhelyezniük "a lapocskák ügyes eltologatásával". Persze bizonyítani nem tudták, hogy nem lehet-e mégtöbbet elhelyezni mégügyesebb módon. Nos engem ez az "ügyes eltologatás" érdekelne. Ki tud erről valamit?
HK
|
| Előzmény: [43] Gubbubu, 2004-01-23 11:53:13 |
|
| [43] Gubbubu | 2004-01-23 11:53:13 |
 Üdvözlök mindenkit, s mivel elég sok választ kaptam a bizonyítási kísérletemre, most ömlesztve válaszolok mindenkinek:
Egyszóval: az utolsó - a fene egye meg, pont az utolsó! - lépést sajnos bosszantóan elnéztem. A folyamat végeredménye (feltéve, ha az előző lépések és a jelen javított verzió hibamentes): 2=n52+n32-2n42. Köszönöm Lórántfy Lászlónak, Pataki Jánosnak és Nádor Péternek (remélem, a nevekre jól tippelek és emlékszem), hogy vették a fáradtságot, átnézték és szóltak, illetve Zormac-nak, hogy foglalkoztak a témával.
Zormacnak annyit: eredetileg én is kongruenciákkal vagy kongruenciarendszerekkel próbálkoztam, de nem azért hagytam abba, mert reménytelennek tűnt a dolog, hanem mert "véletlenül" (különböző megfontolások után) az általam "levezetés"nek mondott gondolatsorra bukkantam. Ha létezik a feladatnak algebrai megoldása, akkor az valószínűleg tényleg valamilyen mod(m) gondolatmenet. Átnézem a táblázatodat, hátha még eszembe jut valami, ami segíthet.
A "marha nehéz problémákról" Erdős Pál egy kollégájának mondott szólása jut az eszembe: "Senkit sem irigyeltem még bizonyításért, de téged irigyellek ezért a sejtésedért". Egy másik: "Nincs elégtétel, ha túl könnyű a tétel". Egy feladat akkor is szép vagy érdekes lehet, ha senki (én sem) tudja megoldani. Természetesen nem az a cél, hogy mindig csak olyan marha nehezeket kérdezzünk, amit senki sem tud megoldani (az elég egyhangú lenne, vannak olyan tanárok, akiknek ez az egyetlen életcéljuk, és én sem szeretem őket), de néha talán megengedhető, különösen a "Nehéz problémák" rovatban.
Üdv:Mészáros Á.
|
|
| [42] Zormac | 2004-01-23 10:42:03 |
 Sziasztok,
a polinomos feladathoz egy apróság, jó kis általános iskolai módszerekkel, szóval valószínűleg semmi komoly nem fog kijönni belőle, esetleg segít, hogy gyorsabb programot írjunk :-). Amúgy én is leprogramoztam, s a  215 intervallumon belül szintén csak a teljes négyzetek jöttek ki. 215 intervallumon belül szintén csak a teljes négyzetek jöttek ki.
Legyen a polinom p(x)=x2+bx+c2 alakú (az trivi, hogy c négyzetszám). Akkor a következő számokról tudjuk, hogy négyzetszámok: c2, c2+b+1, c2+2b+4, c2+3b+9, c2+4b+16.
Ha megnézzük a 4-gyel való oszthatóságot (feltéve mondjuk, hogy c2 x(4)), az alábbi táblázat készíthető: x(4)), az alábbi táblázat készíthető:
[c2 x(4)] x(4)] |
b 0(4) 0(4) |
b 1(4) 1(4) |
b 2(4) 2(4) |
b 3(4) 3(4) |
| c2 |
x |
x |
x |
x |
| c2+b+1 |
x+1 |
x+2 |
x+3 |
x |
| c2+2b+4 |
x |
Ø |
x |
x+2 |
| c2+3b+9 |
x+1 |
|
x+3 |
Ø |
| c2+4b+16 |
x |
|
x |
|
|
Egy oszlopban csak két szomszédos maradékosztály állhat, mert a négyzetszám mod4 csak 0 vagy 1 lehet. Ahol ez a feltétel sérül, ott az oszlopot - az ellentmondást jelző kis villám hiányában :-) - egy Ø jel zárja.
Ha minden jól ment, ebből kijött, hogy b csak páros szám lehet. Máris kétszer olyan gyors a program (hacsak el nem rontottam :-) Persze nem valószínű, hogy van olyan modulus, ami kiadja a bizonyítást, legalábbis én nem találtam ilyet...
z.
|
|
|
| [40] pataki | 2004-01-23 07:47:22 |
 Kedves Gubbubu,
nézd meg még egyszer a legutolsó -- számozatlan -- egyenletedet. (Amikor XI-bôl kivonod a X-et)
Amúgy meg ne aggódj, itt semmi értelme plágiumról beszélni. Bár mielôtt kérdezni kezdesz, érdemes elôbb egy kicsit töprengeni, mert mire észbekap az ember, olyan marha nehezeket bir kérdezni, hogy maga is meglepödik.
Üdvözlettel Pataki János
|
| Előzmény: [34] Gubbubu, 2004-01-22 19:23:14 |
|
| [39] lorantfy | 2004-01-22 23:46:33 |
 Kedves Gubbubu!
Míg futott a program átnéztem a levezetésedet. Jónak tűnik. Holnap még pihenten papíron átnézem. A program sem talált -+32720 közötti együtthatókkal megoldást. 4 helyen jó feltétellel az említett 6 eset jött ki. (Elsőben a c=36-ot elírtam!)
Tulajdonképpen megvan a válasz Patakinak. Ha akarja, majd Ő szűkíti a feladat feltételeit.
Pihend ki magad Te is! Üdv! L.
|
| Előzmény: [38] Gubbubu, 2004-01-22 22:09:17 |
|








 n22 (4).
n22 (4). 
 függvényében.
függvényében. 



 215 intervallumon belül szintén csak a teljes négyzetek jöttek ki.
215 intervallumon belül szintén csak a teljes négyzetek jöttek ki.