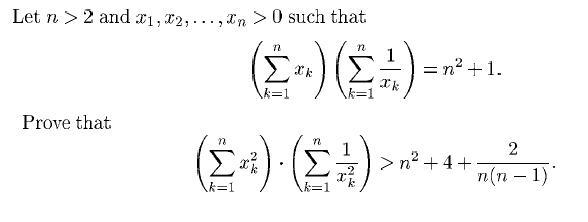| [644] sakkmath | 2009-01-19 19:07:46 |
 Tekintsük az 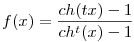 valós - valós függvényt, ahol t valós - valós függvényt, ahol t 3. 3.
1) Határozzuk meg az f függvény aszimptotáját.
2) Határozzuk meg az f görbéje és aszimptotája közötti terület nagyságát.
3) Igaz-e, hogy f inflexiós pontja rajta van az x = 1 egyenesen?
|
|
| [643] epsilon | 2009-01-08 15:05:21 |
 B.Ú.É.K. Mindenkinek! Már hosszú ideje bajlódom a következő feladattal. Egyedüli reményem az maradt, hogy hátha Ti tudnátok segíteni! Előre is kösz, üdv: epsilon
|
 |
|
| [642] Csimby | 2008-12-25 15:54:20 |
 16. tétel, ebben a tematikában szóval biztosan igaz :-) Jegyzetben nem találtam meg, de Gergő barátom szerint:
"...most néztem tanárszakosok anyagát, és abban benne van pontosan 2-vel. A tematikában. A megoldás valami olyasmi hogy jólrendezzük a sík egyeneseit, és tr.f.rekurzuióval definiáljuk a halmazt. De nem tudom, hogy pontosan hogy, gondolkozok. Pl. mindig a soron következőről választunk két pontot, vagy egyet, vagy nullát, attól függ mennyi van már rajta. Hogy ne kerüljön egyikre se több mint 2 pont, válasszuk ezeket úgy h semelyik 3 ne legyen egy egyenesen. Mivel minden lépésben a már meglévő pontok által kifeszített egyenesek száma kisebb mint kontinuum, marad még pont az épp aktuális egyenesen, amit választhatunk. Még az kellene, hogy limesz lépésben mit csináljunk? Hát köpjünk, vagy ilyesmi :)"
|
|
|
| [640] Csimby | 2008-12-25 11:57:24 |
 k=3-ra az x3 fv. szerintem jó. Ennek az x=c típusú egyenesekkel 1 metszéspontja van. Az y=ax+b típusúakkal meg annyi metszéspont lesz, mint x3=ax+b egyenlet valós gyökeinek a száma. Vagyis legalább 1 és legfeljebb 3.
|
| Előzmény: [639] Csimby, 2008-12-25 11:22:02 |
|
|
| [638] Sirpi | 2008-12-25 08:28:17 |
 Kellemes karacsonyt innen is, ha mar hozzaszolok :-)
Azert nem tertem ki a vegtelen esetre, mert nincs ra szukseg. Legalabbis nekem nagyon konnyen sikerult "eleg veges" k-ra megfelelo ponthalmazt gyartanom.
|
| Előzmény: [637] Csimby, 2008-12-24 22:30:25 |
|
| [637] Csimby | 2008-12-24 22:30:25 |
 Boldog Karácsonyt minden fórumozónak!
És hogyha azt mondjuk, hogy minden egyenesen legyen pontja, de legfeljebb megszámlálható sok pontja? Ez még gyengébb feltétel, ez esetben tudunk mondani valamit?
|
| Előzmény: [636] Sirpi, 2008-12-24 22:11:14 |
|
| [636] Sirpi | 2008-12-24 22:11:14 |
 Egy ideje erlelodik bennem egy feladat, de csak most jutottam el oda, hogy kituzzem. Egyelore nem tudom ra a megoldast. Szoval van-e olyan sikbeli ponthalmaz, aminek minden egyenesen van pontja, de mindegyiken legfeljebb ketto. Szerintem ez nehez, de mindjart konnyebb, ha azt irjuk elo, hogy minden egyenesen legalabb 1, es legfeljebb k pontja legyen a ponthalmaznak, ahol k konstans. Mennyi a lehetseges legkisebb k, amire van megfelelo ponthalmaz?
Amugy ha valaki ugy erzi, hogy elvetemult vagyok, hogy szenteste ilyen feladatokon ragodom, akkor annak van nemi igazsaga, de hozzateszem azt is, hogy jelenleg kulfoldon tartozkodom es az ajandekozast mar 20-an letudtam :-) (ezert is nem tudok ekezeteket irni, amiert utolag is bocs).
|
|
|
|
|
| [632] Csimby | 2008-05-25 14:22:09 |
 Amúgy a mail címet miért nem lehet megváltoztatni az adatmódosításnál?
|
|
|
| [630] Sirpi | 2008-05-25 07:54:18 |
 Már csak akkor látod mások (nem rejtett) mailcímét, ha be vagy jelentkezve, így ez már nem indok. Géza pedig sokra megy az infóval, hogy máshol megtalál, mert a regisztrációid nincsenek összekapcsolva.
Továbbra sem értem, hogy miért van szükséged erre a hozzáállásra, folyton támadsz, minősíthetetlen hangnemben tálalod a véleményed (pl. egy szó kimarad egy példából és máris "ultragagyi"-kat és hasonlókat pufogtatsz), de rád nem tehet megjegyzést senki. Legközelebb már nem fogom a fórumot zavarni, hogy megint szólok (vannak ennél érdekesebb témák is), helyette lesz egy kis időd gondolkodni (ha észrevételed van, akár a - publikus - mailcímemet is használhatod).
Ha mindenki szembejön Veled az autópályán, akkor nem biztos, hogy ők tévesztették el a sávot.
|
| Előzmény: [629] Róbert Gida, 2008-05-24 23:05:46 |
|
| [629] Róbert Gida | 2008-05-24 23:05:46 |
 A bankszámlaszámom/jelszavam nem kell? A regisztrációnál nincs is odaírva, hogy az eredeti nevünket használjuk. Egyébként én speciel nem is gondoltam rá, kb. 10 fórumon vagyok fent, van olyan, ahol névvel, fotóval, emailcímmel együtt, ahol kb. minden 10-edik ember adta meg a valódi nevét. Úgyhogy nem kell leordítani.
Spamek miatt sem publikus az emailcímem,az adatlapra kattintva kiírja ugyanis azt.
|
| Előzmény: [628] BohnerGéza, 2008-05-24 21:57:01 |
|
|
| [627] Róbert Gida | 2008-05-24 20:51:52 |
 Ez egyébként baromi ismert példa. Most néztem, a Konkrét Matematika című könyvben 6.43-as példa.
De a Mathematica programban a help menüben példaként is szerepel. Bár kipróbálva kb. 10 másodperc mire kiszámolja. Pedig 2 mértani sor összegeként felírva a példa triviális.
|
| Előzmény: [626] jonas, 2008-05-24 16:07:31 |
|
|
|
| [623] huber | 2008-05-24 13:51:21 |
 Ákos!
Köszönöm a segítséget!
huber
|
|
|
| [620] huber | 2008-05-24 13:12:25 |
 Üdv! Új vagyok és tapasztalatlan. Tudna valaki nekem segíteni? Egy végtelen sor összege vár rám: szumma fn/(10 az n+1. hatványon). A sor specialitása, hogy a számláló a Fibonacci sorozat elemeit tartalmazza, bár lehet, hogy csak az egész számokat? talán értem a feladatot, nem tudom...
Kérek segítséget!
huber
|
|
| [619] jonas | 2008-05-24 12:19:13 |
 Rondán néz ki a felírása, de szerintem ha átírod komplex összeggé, akkor a mértani sorokat összegezni lehet. Remélem, jól gondolom.
|
| Előzmény: [618] PAL, 2008-05-23 21:20:18 |
|
| [618] PAL | 2008-05-23 21:20:18 |
 Sziasztok!
Nem tudom, jó témához írom-e kérdésem, de számomra az egyik gyakorlaton kapott alábbi 2 állítás bizonyítása sajnos túlságosan is nehéznek bizonyult, aki tud kérem segítsen. Előre is köszönöm.
|
 |
|



 3.
3.