| [75] Sirpi | 2004-02-17 08:51:41 |
 Sziasztok!
Ha minden igaz, ezen a fórumon még nem szerepelt ez a feladat, úgyhogy kitüzöm:
Adott n és m pozitív egészekre legfeljebb hány egész számot lehet megadni úgy, hogy bármely egymás után következö n összege szigorúan pozitív, míg bármely egymás utáni m összege szigorúan negatív legyen?
|
|
| [74] Csizmadia Gábor | 2004-02-16 22:34:40 |
 A feladat egyszerű addíciós tétellel kijön, de azért szerintem ez is szép: Legyen z=a+bi komplex szám. Jelölje z arkuszát
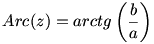
abszolút értékét
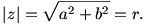
Könnyen bizonyítható az alábbi egyszerű tétel:
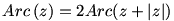
Vegyünk fel egy derékszögű koordinátarendszert, és a z, illetve z+|z| számoknak megfelelő (a;b) és (a+r;b) pontokat. Ekkor (0;0), (a;b), (a+r;b), (r;0) pontok egy rombuszt alkotnak, aminek a (0;0)-n és (a+r;b)-n átmenő egyenes átlója, tehát ennek az egyenesnek az x-tengellyel bezárt szöge valóban fele a (0;0)-n és (a;b)-n átmenő egyenes x-tengellyel bezárt szögével. (qed) Mármost
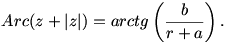
Az
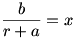
helyettesítéssel
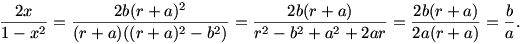
Tehát
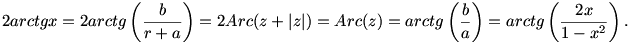
|
| Előzmény: [73] Csizmadia Gábor, 2004-02-16 21:35:35 |
|
| [73] Csizmadia Gábor | 2004-02-16 21:35:35 |
 Bocsánatot kell kérnem, ezt nem ide kellett volna beraknom, mert így a feladat egy kicsit egyszerű. Egy bonyolultabb (de valószínűleg az ide járók többsége által ismert) feladat "melléktermékeként" jött ki ez a tétel, és nem gondoltam bele, hogy ez annál sokkal egyszerűbb úton is bizonyítható.
|
| Előzmény: [72] Csizmadia Gábor, 2004-02-16 18:25:19 |
|
| [72] Csizmadia Gábor | 2004-02-16 18:25:19 |
 Szerintem ez a feladat (mármint maga a tény, és a bizonyítása is) nagyon szép:
Bizonyítsd be, hogy x (-1;1)-re érvényes az alábbi összefüggés: (-1;1)-re érvényes az alábbi összefüggés:
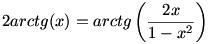
Üdv: Csizmadia Gábor
|
|
| [70] Hajba Károly | 2004-02-12 09:28:28 |
 Kedves gubbubu!
Fáradozásodat én is köszönöm, de az egészséged fontosabb, kúráld ki magad előbb. Addig is megleszünk a megoldás nélkül, mint ahogy eddig is tudtunk élni nélküle. Legalább arra inspirál, hogy újabb ötletek fel- és elvetésével tovább gondolkodjunk a problémán.
Ha lesz egy kis időm, beírom az eddigi kutatásaim eredményeit egy kis kritikára.
HK
|
| Előzmény: [68] Gubbubu, 2004-02-11 18:54:04 |
|
| [69] lorantfy | 2004-02-12 07:46:02 |
 Kedves Gubbubu!
Javulást kívánok Neked! Remélem végülis sikerrel jársz a keresésben, mert már nagyon fúrja az oldalam a kiváncsiság! Én is próbálkozom matematikus ismerőseim körében.
|
| Előzmény: [68] Gubbubu, 2004-02-11 18:54:04 |
|
| [68] Gubbubu | 2004-02-11 18:54:04 |
 Kedves Onogur!
Sajnos, eddigi kutatásaim jobbára negatív eredménnyel jártak, még van egy-két tippem, hol járjak utána, de lehetséges, hogy Magyarországon vagy legalábbis Budapesten vagy legalábbis az ELTÉ-n nincs meg az Erdős-Graham négyzetpakolásos cikk példánya. Most tartok néhány nap szünetet, mivel egy hete már hogy elkapott az "infulenzia" (szerencsére úgy látszik, nem a madárinfluenza, mivel még úgy-ahogy élek), jövő héten még elmegyek egy-két helyre ez ügyben, de lehet, hogy önerőből kell megismételnünk Erdős és Graham bravúrját.
Üdv: G.
|
|
| [67] Zormac | 2004-02-09 15:59:23 |
 Sziasztok,
ez biztos lerágott csont, de mégsem igazán leltem rá a weben a megoldás(ok)ra...
Szóval a probléma azt hiszem már annyiból is ismert, hogy "Szindbád és a nők". Azért leírom:
Szindbád feleséget akar magának választani 100 adott hölgy közül. A folyamat a következő: egymás után elvonulnak előtte a hölgyek (libasorban :-), és Szindbád tetszőleges pillanatban azt mondhatja, rámutatva az épp színe előtt álló hölgyre, hogy "őt akarom!". Ha egy hölgyet nem választott ki, az elment örökre, később már nem térhet vissza rá. Miután választott, a hátralevőket már nem nézi meg (bár ez nem lényeges).
Főhősünk nyilván minél jobb nőt akar, ámde ez is legalább kétféleképp fogalmazható meg:
1) Minden hölgy "szépsége" leírható egy tetszésindexszel (mint számmal, mondjuk 0 és 10 között) és Szindbád maximalizálni akarja ezt a bizonyos számot.
2) Szindbád minél nagyobb eséllyel A LEGSZEBB nőt akarja (speciális esete az előzőnek, ha mondjuk egy kivétellel mindegyik tetszésindex 0).
A második esetre közszájon forog a következő eljárás (azt hiszem, M-stratégia a neve): az első M hölgyet biztosan nem fogja kiválasztani, majd a maradékból kiválasztja az elsőt, aki az első M mindegyikénél szebb; ha nincs ilyen, kiválasztja az utolsót (és boldogtalan lesz).
Tehát a feladatok:
a) Határozzuk meg M azon értékét, amelyre a legnagyobb eséllyel válaszja ki a legszebb hölgyet (ez emlékeim szerint nem túl nehéz, viszont az eredmény "szép").
b) Igaz-e, hogy az M-stratégia, mint módszer, valóban helyes? Azaz, van-e más stratégia, amely az a) részben adódó valószínűségnél jobbat ad?
c) Vajon mi a helyzet az 1), általánosabb esetben?
z.
ps. aki mondjuk mostanság próbál nagyobb lakást, neadjisten házat venni, talán átérzi e feladat Életre kivetített mondanivalóját :-)
|
|
| [66] Csimby | 2004-02-04 10:59:04 |
 Kedves Onogur!
Szerintem az eddig talált legkisebb s-ek vannak fönt azon a lapon, de mivel ezeket a dolgokat nehéz bizonyítani (és szerintem ők sem tették meg) lehet, hogy a tiéd jobb...
|
|
| [65] Hajba Károly | 2004-02-04 10:26:31 |
 Kedves Csimby!
Az első linkedbeli méretek az eddig talált legkisebbeket mutatja?
Úgy tűnik, hogy én az 50 kockát el tudom helyezni kisebb helyre is, mint David Cantrell 2002. augusztusi "találása". Épp egy hasonló feladatot barkácsoltam össze, s a megoldást csak tovább kellett finomítani. s=7,620+ helyett s=7,599-, de még át szeretném számolni; sőt az 52-esre van egy teljesen más elosztású is pontosan ugyanakkora méretben.
Mindamellett az a sejtésem, hogy a közel 45 fokos elforgatással 1.000.000,25 alatti méretben újabb elemet nemigen tudunk behelyezni. Itt valami más jellegű csavarásos megoldás jöhet számításba, melyet kisebb méretben még nem lehet alkalmazni, így elképzelni is nagyon nehéz. Néhány elképzelést végigszámoltam, de nem váltak jó elképzelésnek.
HK
|
| Előzmény: [62] Csimby, 2004-02-03 00:14:51 |
|
| [64] Hajba Károly | 2004-02-03 13:54:45 |
 Kedves Csimby!
Kösz a címeket. A másodikra el is kalandoztam, s ráleltem egy a GEOMETRIA topikban feltett feladatomra is.
De nagyon érdekes az n egységkör ill. egységnégyzet elhelyezéséhez szükséges legkisebb négyzetek keresése is.
De hát hol van ez még a billiótól? :o)
HK
|
| Előzmény: [62] Csimby, 2004-02-03 00:14:51 |
|
|
| [62] Csimby | 2004-02-03 00:14:51 |
 Üdv!
Akik a parkettázós feladattal foglalkoznak (adott négyzetbe hány egységnyi kisnégyzet fér?) azoknak szeretnék néhány király címet mondani:
http://www.stetson.edu/ efriedma/squinsqu/
http://mathworld.wolfram.com/SquarePacking.html
|
|
| [61] pataki | 2004-02-01 06:54:00 |
 Kedves László, örülök, hogy a kérdés felkeltette az érdeklôdést (bár a "bárányok még hallgatnak", ami lehet reménykeltô is) én már egy ideje gondolkodom rajta. Mint a kitüzésembôl is kiderült,és igy remélem,hogy fair a játék, nem ismerek megoldást 5 szomszédos négyzetszám értékre.
Nem ismerek olyan eredményt sem, ami egyáltalán korlátot adna, hogy hány szomszédos helyen vehet föl négyzetszámot egy ilyen polinom, sôt, azt sem tudom, hogy van-e ilyen korlát. Úgy értem, minden n-hez lehet olyan polinom, ami n szomszédos helyen négyzetszám. (Az itt nem érdekes, hogy a dolog a nulláról indul, mert az elsôfokú tag együtthatója páros és igy el lehet tolni.) Szóval innen is lehetne támadni.
Van ugyan némi ködös kontextus, amiben az 5-nek van értelme, de teljesen homályos. Azért nem irom le, amit tudok, mert az befolyásolhatna másokat és itt fontos a friss fej, persze lehet, hogy nincs igazam. Másfelôl lényegében nem sokat tudok. Mindenesetre ha van megoldás, akkor az jó nagy. És akkor persze jönne a 6.
Ehhez a diofantikus megközelítéshez annyit, hogy ha nem építi be az ember a nemnulla diszkrimináns feltételt, akkor le kell kezelni a végtelen sok triviális megoldást. A te k-d egyébként jó jelzôszám, mert a diszkrimináns negyede. No ennyi. Üdvözlettel Pataki János
|
| Előzmény: [60] lorantfy, 2004-01-31 21:58:38 |
|
| [60] lorantfy | 2004-01-31 21:58:38 |
 Kedves Fórumosok!
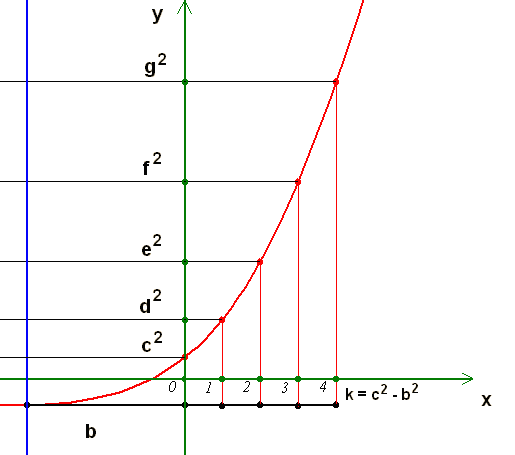
Apró ötlet a négyzetszámos polinomos példához. Hátha valaki kihoz belőle valamit, mert nekem sajnos most nincs időm rá: x2+Bx+C a másodfokú polinomunk. Eddig beláttuk, hogy B páros, így legyen B=2b és C=c2, hogy x=0-nál négyzetszám legyen az értéke.
Legyen k=b2-c2.
x2+2b+c2=(b+x)2-b2+c2=(b+x)2-(b2-c2)=(b+x)2-k
Az x=0,1,2,3,4 helyen felvett értékek: c2,d2,e2,f2,g2
c2=b2–k
d2=(b+1)2–k
e2=(b+2)2–k
f2=(b+3)2–k
g2=(b+4)2–k
5 egymás után következő egész szám négyzetéből kivonva ugyanazt a k egész számot újra négyzetszámokat kell kapnunk!
A négyzetszámok utolsó számjegye csak 0,1,4,5,6,9 lehet. A 0,1,2,3,4,5,6,7,8,9 utolsó számjegyekhez a 0,1,4,9,6,5,6,9,4,1 négyzetszám végződések tartoznak. Ezekből 5 egymásutánit (ciklikusan) kiválasztva és levonva belőle k utolsó számjegyét csak akkor kaphatunk mind az ötnél négyzetszám végződést, ha k szám 0-ra vagy 5-re végződik.
Tehát 5| k. Az egymás utáni 5 szám közül (b, b+1, b+2, b+3, b+4) egy biztos osztható 5-tel, vagyis négyzete osztható 25-tel. Ekkor viszont a bal oldalon álló megfelelő négyzetszám is oszható 5-tel, tehát 25-tel is. Így k két 25-tel osztható négyzetszám különbsége: 25| k.
Ha belátnánk még, hogy k páros, (vagy esetleg 4-el osztható), akkor a végén 0 (vagy két 0) áll. Így c, d, e, f, g számok négyzeteinek utolsó számjegye (vagy utolsó 2 számjegye) sorra egyenlő b, b+1, b+2, b+3, b+4 négyzeteinek utolsó jegyeivel. Ebből talán ellentmondásra lehetne jutni.
|
 |
| Előzmény: [56] Gubbubu, 2004-01-27 00:33:01 |
|
| [59] Gubbubu | 2004-01-27 20:20:55 |
 Elnézést - mielőtt bárki belém kötne - az "iletve" szót véletlenül (billentyűzetergonómiai gondok miatt) írtam egy l-lel! Helyesen: "illetve".
Üdv 1:00 körül: G.
|
| Előzmény: [58] Gubbubu, 2004-01-27 19:05:15 |
|
| [58] Gubbubu | 2004-01-27 19:05:15 |
 Kedves Kós Géza!
"4|B" nem egy állítás volt, hanem - ezek szerint nem egészen igaz - sejtés, ami - természeténél fogva - nem megindokolva, hanem inkább kérdezve van (iletve volt)! Nem csoda, ha nem érted, mivel ami nincs, az kicsit nehezebben érthető, mint ami van!
Üdv:G.
|
| Előzmény: [57] Kós Géza, 2004-01-27 16:32:35 |
|
| [57] Kós Géza | 2004-01-27 16:32:35 |
 A 4-gyel oszthatóság indoklását nem értem.
Az ilyen sejtéseket mindig érdemes tesztelni az olyan triviális megoldásokon, mint például x2+2x+1=(x+1)2. Ez a példa is mutatja, hogy a diszkrimináns vizsgálata nélkül nem jöhet ki, hogy a b a 2-n kívül bármivel is osztható.
|
| Előzmény: [56] Gubbubu, 2004-01-27 00:33:01 |
|
| [56] Gubbubu | 2004-01-27 00:33:01 |
 Kedves Algebristák!
A négyzetszám értékű polinommal annyira sikerült előrejutnom, hogy sikerült igazolnom Zormac immár klasszikus eredményeit, miszerint a konstans tag négyzetszám, és az elsőfokú tag együtthatója páros. Ezeket most gyorsan és röviden belátom. A feltétel miatt p(0) négyzetszám, c2=02+0.x+C, azaz C=c2. Azaz p(x)=x2+Bx+c2. Ekkor a négyzetszámértékűségi feltételek a következőket jelentik:
I. 1+B+c2=n12;
II. 4+2B+c2=n22;
III. 9+3B+c2=n32;
IV. 16+4B+c2=n42;
Ám a II. egyenletből 2B+c2 n22 (4). n22 (4).
x y (m) fogja jelölni, hogy x és y m-mel osztva azonos maradékot ad, azaz a mod(m) kongruenciát, a továbbiakban mindig mod(4) lesz a kongruencia, így nem írom ki a modulust). y (m) fogja jelölni, hogy x és y m-mel osztva azonos maradékot ad, azaz a mod(m) kongruenciát, a továbbiakban mindig mod(4) lesz a kongruencia, így nem írom ki a modulust).
És mivel B 0,1,2,3 esetén rendre 2B 0,1,2,3 esetén rendre 2B 0,2,0,2, ehhez a mod(4) 0-val vagy 1-gyel kongruens c2 számot adva rendre 0,2,0,2-t vagy 1,3,1,3-t adva a kapott szám (n22) is négyzetszám, vagyis mod(4) 0 vagy 1, amiből látható, hogy az első esetben (ha c2 0 modd(4)) is a 0,2,0,2 esetekből csak a 0-s esetek jöhetnek szóba, vagyis ha B 0 vagy 2 mod(4), azaz páros, és ugyanez van, ha az 1,3,1,3 lehetőséget nézzük (azaz ha c2 1 mod(4)). 0,2,0,2, ehhez a mod(4) 0-val vagy 1-gyel kongruens c2 számot adva rendre 0,2,0,2-t vagy 1,3,1,3-t adva a kapott szám (n22) is négyzetszám, vagyis mod(4) 0 vagy 1, amiből látható, hogy az első esetben (ha c2 0 modd(4)) is a 0,2,0,2 esetekből csak a 0-s esetek jöhetnek szóba, vagyis ha B 0 vagy 2 mod(4), azaz páros, és ugyanez van, ha az 1,3,1,3 lehetőséget nézzük (azaz ha c2 1 mod(4)).
Tehát B páros, így a B=2b jelöléssel írható p(x)=x2+2b+c2.
Megjegyzés: Figyeljük meg, hogy itt felhasználtuk, hogy a konstans tag négyzetszám.
Azt állítom, innen elindulva mod(8) be lehet látni, hogy b is páros, azaz B 4-gyel is osztható. Örülnék, ha mások is megerősítenének ebben.
Újra felírva a négyzetszámértékűségi feltételeket:
I. 1+2b+c2=n12;
II. 4+4b+c2=n22;
III. 9+6b+c2=n32;
IV. 16+8b+c2=n42;
I.-IV. alapján az is látható, hogy c2,n22,n42 kongruens mod(2), míg c2+1,n12,n32 is kongruens mod(2), és e két osztály elemei persze inkongruensek. Persze ugyanez mondható el e négyzetszámok "gyökeire" is.
Hát egyelőre csak ennyi... nem olyan sok... de még nem adtam fel...
Üdv mindenkinek:G.
|
|
| [55] Gubbubu | 2004-01-26 19:20:34 |
 Kedves Onogur!
A "közvetítői szerepemmel" kapcsolatos pozitív vagy (remélem, nem) negatív eredmény vagy e hét csütörtök, vagy jövő hét hétfő, de legkésőbb február 9. után egy-két nappal várható. Addig tehát biztosan nyugodtan "sütögethetitek" Lászlóval a kérdéses "négyzetzsúfolási" bizonyítást.
A másik úton, az interneten más d. geometriai tétel kapcsán már végeztem elég hosszadalmas kereséseket úgy egy fél éve, minden eredmény nélkül (még angol nyelvű cikkivonatokat vagy lényeges utalásokat sem találtam, nemhogy magyar nyelvű vagy rajzzal illusztrált cikkeket). Most majd megpróbálom néhány újabb keresőszóval (pl. Voronoi, Erdős-Graham, Graham stb.). A d. geometria nagyon fiatal (alig száz éves) tudományág, úgy tudom, még tankönyve sincs, tehát ez az eredménytelenség csak közepes mértékben meglepő.
Üdv. G.
|
| Előzmény: [50] Hajba Károly, 2004-01-26 00:01:18 |
|
| [54] lorantfy | 2004-01-26 15:58:57 |
 Kedves Károly!
Én is arra gondolok hogy egyre növekvő, persze nagyon kicsi elfordítások és apró eltolások vezetnek majd a megoldáshoz. Nyilván az a cél, hogy a külső üres sávból lefoglalt területeket befelé illetve "összetereljük". A belső négyzetek között is lesznek apró rések, de ezek összege kisebb lesz mint a kívül lefoglalt terület. Sorozatocskákat kell majd összegezni!
|
| Előzmény: [53] Hajba Károly, 2004-01-26 13:40:37 |
|
| [53] Hajba Károly | 2004-01-26 13:40:37 |
 Kedves László!
Örülök, hogy sikerült felpiszkálni az érdeklődésedet a téma iránt. Így már nem vagyok egyedül. :o) Én már vagy két éve vissza-visszatérek e témához alkalmanként, ...de hát nem én vagyok a PRÍM.
Arra már rájöttem, hogy 45°-os elfordítással csak akkor lehet alkalmas méret esetén megoldást találni, ha 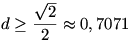 Pl.: 999.996,78 méret esetén 133.584 az elforgatott lapocskák esetén a többlet. De hát a d itt majd' 8-szoros. Továbbá kisebb méretek esetén vagy 0°-os vagy 45°-os elforgatott elemek esetén lehet 'jó' kitöltést találni. A köztes szögek a tapasztalatom szerint rontják a lehetőséget. Pl.: 999.996,78 méret esetén 133.584 az elforgatott lapocskák esetén a többlet. De hát a d itt majd' 8-szoros. Továbbá kisebb méretek esetén vagy 0°-os vagy 45°-os elforgatott elemek esetén lehet 'jó' kitöltést találni. A köztes szögek a tapasztalatom szerint rontják a lehetőséget.
Gyanítom, hogy a megoldásban minden elem egy kicsit jobban el van fordítva, de hát ezt legalább 3200-as méret esetén már számomra követhetetlen, kis méret esetén pedig még nem csökken a helyigényük.
Mindentől függetlenül Sirpi által vázolni próbált és általunk továbbgondolt eset is vezethet sikerre. Ki tudja?
Aki tudja szóljon!
HK
|
| Előzmény: [52] lorantfy, 2004-01-26 08:50:23 |
|
| [52] lorantfy | 2004-01-26 08:50:23 |
 Kedves Károly!
Sikerült rendesen felpiszkálnod az érdeklődésemet a téma iránt. Az az érzésem, hogy az eredeti megoldás megértéséhez is fel kell kötni a gatyánkat!
Gondolom a könyv szerzője is azért egyszerűsítette ilyen talányosan a műveletet: "ügyesen elcsúsztatva őket egymás mellett"-re, mert nem lehet pár mondattal egyszerűen megadni az eljárást.
Én arra gondoltam az előző megoldási kisérletemben, hogy az 1 fokos elforgatás után az oszlopok eltolásával a sarkokat CD vonalra lehet hozni és igy alul is illeszkedni fognak a négyzetek sarkai.
Csakhogy ezután ugyanezt keresztirányban már nem lehet megtenni.
|
| Előzmény: [51] Hajba Károly, 2004-01-26 01:13:06 |
|
| [51] Hajba Károly | 2004-01-26 01:13:06 |
 Kedves László!
Ha jól sejtem a CM vonal mentén közel 500.000 darab parkettát érint a belemetszés és az MF mentén egyáltalán nem vagy nagyon-nagyon keveset lehetne még többletként beillszteni. Ehhez képest a végén csak kb. 10 %-nyi új hely keletkezik. S ez nem sokat változik a szög mértékének módosításával sem.
A pontosabb itélethozatalhoz képleteket kellene felállítani  függvényében. függvényében.
De kiváncsi vagyok a Te észrevételedre is.
HK
|
| Előzmény: [49] lorantfy, 2004-01-24 10:28:59 |
|
| [50] Hajba Károly | 2004-01-26 00:01:18 |
 Kedves gubbubu!
Van egy sanda gyanúm, hogy a probléma nehezebben fog megoldódni, mint első ránézésre tűnik. Ezért közvetítői szereped nem felesleges, mit előre is köszönök.
Tehát "...1975-ben, a kombinatorikával foglalkozók legnagyobb meglepetésére és örömére Erdősnek és Grahamnek mégis sikerült nem 1, de több mint 100 ezer újabbat rakni a kezdeti 1 billió parkettához, ügyesen elcsúsztatva őket egymás mellett. Graham szerint az 1.000.000.100.000 parkettás megoldással közel jutottak az optimálishoz, a két matematikus mégsem tudta bebizonyítani, hogy ezzel a módszerrel lehet a leghatékonyabban kis négyzetekkel nagy négyzeteket lefedni. Két évtized múlt el, de az ő eljárásuk még mindig nem tudták jobbal felváltani. Nincs elégtétel, ha túl könnyű a tétel."
Azóta már lassan 30 év is eltelt, továbbá a fenti idézet előtt a könyv azt írja, hogy szabálytalan idomok esetén nem találnak hatékony stratégiát ill. a matematikai szakirodalom nem foglalkozik e (szabálytalan idomú lefedés) problémával. E témában a hálón bármilyen rajzzal illusztrált irodalom érdekel, ha fel tudsz ilyent kutatni.
HK
|
| Előzmény: [47] Gubbubu, 2004-01-23 18:27:29 |
|




 (-1;1)-re érvényes az alábbi összefüggés:
(-1;1)-re érvényes az alábbi összefüggés: 






 n22 (4).
n22 (4).  függvényében.
függvényében.