|
| [768] Sinobi | 2014-08-05 23:34:03 |
 * ha lezezik 3 ilyen egyenes, akkor vegtelen sok van.
|
|
| [767] jonas | 2014-08-05 22:52:06 |
 Ezt nem igazán hiszem.
Végy egy tetszőleges ellipszist, és rajta egy pontot. Tükrözd az egyenest erre a pontra, így kapsz egy második ellipszist. A két ellipszis akkor ebben a pontban érinteni fogja egymást. A ponton átmenő majdnem bármely egyenes a két ellipszisből ugyanolyan hosszú szakaszokat metsz ki, hiszen a két szakasz egymás tükörképe a pontra.
|
| Előzmény: [766] Sinobi, 2014-08-05 20:50:01 |
|
| [766] Sinobi | 2014-08-05 20:50:01 |
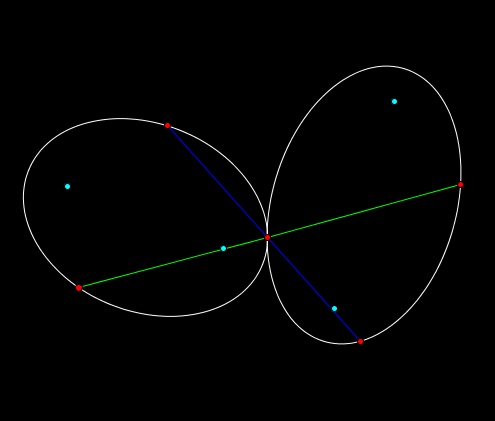
 Talan egy kicsit tul egyszeru ebbe a temaba, de az elozot se lotte le senki.
Bizonyitsd be, hogy ket erintkezo ellipszishez (az erinton kivul) maximum ket olyan egyenes letezik az erintesi ponton at, amely ugyanolyan hosszu szakaszokat metsz ki az ellipszisekbol!
abra:
|
 |
| Előzmény: [704] Sinobi, 2013-09-21 18:43:58 |
|
| [765] w | 2014-06-28 15:20:13 |
 És mindez sima De Moivre-képletes játszadozással jön ki (elég az azonosságot &tex;\displaystyle x\in [-1;+1]&xet; esetén belátni, vagyis &tex;\displaystyle x=\cos t&xet; helyettesítéssel). Mint ez vagy ez, csak sokkal egyszerűbb.
|
| Előzmény: [764] Lóczi Lajos, 2014-06-24 22:16:34 |
|
|
| [763] w | 2014-06-24 10:38:44 |
 Legyen &tex;\displaystyle T_n(x)&xet; és &tex;\displaystyle U_n(x)&xet; rendre az &tex;\displaystyle n&xet;-edik elsőfajú és másodfajú Csebisev-polinom. Bizonyítsuk be (vagy cáfoljuk/javítsuk ki, ha esetleg rosszul írtam le) a következő azonosságot:
&tex;\displaystyle 2\sum_{k=1}^n T_k(x)^2=(n-1)+U_n(x)T_n(x)=n+\frac{T_{2n+1}(x)}{2x}.&xet;
|
|
| [762] csábos | 2014-05-21 15:48:02 |
 &tex;\displaystyle (x^2-\frac{1}{2}y^2-\frac{1}{2}z^2-\frac{3}{2}xy+\frac{3}{2}yz)^2 + \frac{3}{4}( y^2-z^2-yz+2zx-xy)^2
= (x^2+y^2+z^2)^2 -3x^3y-3y^3z-3z^3x&xet;
|
| Előzmény: [739] w, 2013-11-29 22:31:58 |
|
| [761] jonas | 2014-02-17 23:18:13 |
 Az S tartományt algebrai görbe (vagy annak egy része) határolja? Vagyis azon z pontok halmazát keressük, amelyre az f valamelyik gyöke pontosan 1 abszolútértékű. Én azt hiszem, hogy ez egy algebrai görbe, de nem tudom, hogy mennyire könnyű explicit módon fölírni, és hogy hányadfokú lesz.
|
| Előzmény: [760] Lóczi Lajos, 2014-02-17 15:12:07 |
|
|
| [759] marcius8 | 2014-01-24 12:46:40 |
 Még egy újabb kérdés jutott az eszembe, de ez már geometria. Adott három egyforma sugarú és végtelen hosszú henger. A hengerek forgástengelyei páronként egymásra merőlegesek és egy pontban metszik egymást. Tekintsük azt a testet, amely egyenlő a három henger közös részével (metszetével). Mekkora ennek a testnek a felszíne és a térfogata?
|
|
| [758] marcius8 | 2014-01-24 12:42:16 |
 Egy újabb kérdés jutott az eszembe.
A.) Aprajafalván a toronyóra mutatói (kismutató és nagymutató) cm-ben mérve egész számok. 3 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. 2 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. Mekkora lehet a két mutató hossza?
B.) Aprajafalván a toronyóra mutatói (kismutató és nagymutató) cm-ben mérve egész számok. 3 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. 4 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. Mekkora lehet a két mutató hossza?
Ráadásként:
C.) Aprajafalván a toronyóra mutatói (kismutató és nagymutató) cm-ben mérve egész számok. 2 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. 4 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. Mekkora lehet a két mutató hossza?
Ha valakinek van ezeknek a kérdéseknek a megoldásához ötlete, azt előre is köszönöm. Bertalan Zoltán.
|
|
| [757] aaaa | 2014-01-23 20:36:23 |
 Legyen E(X) a keresett várható érték, és keressük a k fej egymás utáni dobásának várható értékét. Ezt megfeltételezzük (feltételes várható érték tulajdonságai miatt ez menni fog), mégpedig az alapján, hogy az első írásig hány fejet dobunk. Ekkor teljesül
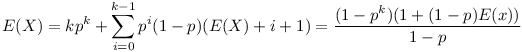
(Az összeget deriválást alkalmazó trükkel lehet könnyen számolni) Ezt kell megoldani E(X)-re, ekkor kapjuk, hogy
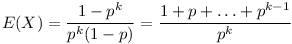
|
| Előzmény: [756] Liklihood, 2014-01-16 13:41:28 |
|
| [756] Liklihood | 2014-01-16 13:41:28 |
 A következő feladat megoldásában kérném a segítségeteket. Legyen egy cinkelt pénzérménk, melyre P(fej)=p=1-P(írás), ahol 0<p<1. Várhatóan hanyadik dobásra következik be, hogy 5 fejet dobunk egymás után?
Válaszaitokat előre is köszönöm. :)
|
|
| [755] marcius8 | 2014-01-07 10:14:14 |
 Köszönöm a hozzászólást. Igazából csak addig jutottam én is, hogy hogyan nézhet ki egy ilyen gráf, és arra jutottam, hogy egy ilyen gráf diszjunkt körökből áll. Tisztelettel: Bertalan Zoltán.
|
| Előzmény: [753] aaaa, 2013-12-23 01:12:02 |
|
| [754] aaaa | 2013-12-23 02:19:16 |
 Némi elírás, a megadott képlet minden gráfra számol, és l-et 3-től kell indítani.
Javítás páros gráfra
Párosra csak a páros tagokat kell összegezni, ezeket is csak 2-től kezdve, így a következőképpen módosulnak a dolgaink:
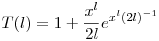
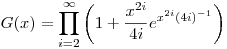
És G(x)-ben xn együtthatója adja meg a sorrendek számát n!-al osztva.
|
| Előzmény: [753] aaaa, 2013-12-23 01:12:02 |
|
| [753] aaaa | 2013-12-23 01:12:02 |
 Egy előzőhöz hasonló gondolatmenettel valahogy így kellene:
Most irányított gráfra csináljuk: Ha meg meg vannak különböztetve a csúcsok, akkor ugye ezeknek n! sorrendje van. Ezt ugye daraboljuk egy partíció szerint. Mit számolunk többször? Hát, ha ugyanazok a csúcsok más sorrendben, de ugyanabban a ciklikus permutációnak megfelelő sorrendben vannak, illetve ha ugynakkora méretű halmazaink vannak, csak más sorrendben. Most generátorfüggvényt csinálunk, 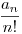 -ra: -ra:
Először csak azt vesszük bele a játékba, hogy k darab ugyanakkora halmazt (k-1)! alkalommal számoltunk, vagyis a hatványsora valahogy így nézzen ki egy tényező:
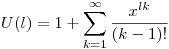
Viszont ezeknek lk darab egymástól független, ugyanolyan gráfot eredményező sorrendje van, tehát:
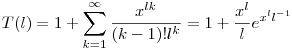
A keresett generátorfüggvény tehát úgy áll elő, hogy a
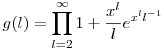
Szorzat xn-hez tartozó együtthatóját szorozzuk n!-al, és elvileg készen kellene lennünk. Ha meg irányításfüggetlen, akkor ennek pontosan a fele jó sorrend, ekkor
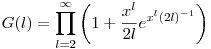
|
| Előzmény: [752] aaaa, 2013-12-23 00:24:11 |
|
| [752] aaaa | 2013-12-23 00:24:11 |
 Kb. 2 percet gondolkozva rajta a következőre jutottam: Mivel a gráf páros, minden kör 2k hosszú, ahol k 2, és ez elég is a párossághoz. Címkézetlen csúcsokon vagyunk, így lényegében n pont partíciónak a száma a kérdés, ahol minden egyes részhalmaz legalább 2 elemet tartalmaz. Ennek a generátorfüggvénye meg: 2, és ez elég is a párossághoz. Címkézetlen csúcsokon vagyunk, így lényegében n pont partíciónak a száma a kérdés, ahol minden egyes részhalmaz legalább 2 elemet tartalmaz. Ennek a generátorfüggvénye meg:
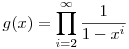
Aminek a hatványsorának xi-hez tartozó együtthatója épp a 2i-re a nem izomorf fák számát. Ennek első néhány tagja:
g(x) 1+x2+x3+2x4+2x5+4x6+4x7+7x8+8x9+12x10+14x11+21x12+24x13+34x14+41x15+55x16+66x17+88x18+105x19+137x20+O[x]21 1+x2+x3+2x4+2x5+4x6+4x7+7x8+8x9+12x10+14x11+21x12+24x13+34x14+41x15+55x16+66x17+88x18+105x19+137x20+O[x]21
Itt megtalálod a sorozat néhány következő tagját. Szerintem ez megadja az izomorfia erejéig a jó gráfok számát, csak ki kell fejteni. Azt nem hinném, hogy ennél sokkal explicitebb képlet létezik, mivel azt írja, hogy P(n+1)-P(n) sorozat ez lesz, ahol P(n) a partíciók száma. Kicsit fáradt vagyok már, szóval lehet, hogy valamit elnéztem.
|
| Előzmény: [750] marcius8, 2013-12-20 10:04:05 |
|
| [751] csábos | 2013-12-22 23:35:36 |
 Nem értem a kérdést. Adott a páros gráf? Akkor mik az élei? Ha nem adott, akkor adott két db n-elemű halmaz, és ezen hány olyan páros gráf van, amely diszjunkt körök uniója? Ha a gráf adott, meg kell-e őrizni a paritását?
|
| Előzmény: [750] marcius8, 2013-12-20 10:04:05 |
|
| [750] marcius8 | 2013-12-20 10:04:05 |
 Tekintsünk egy páros gráfot, melynek "2n" csúcsa van. Hányféleképpen lehet ebbe a páros gráfba berajzolni az éleket, úgy hogy minden csúcs foka 2 legyen? Kicsit nehezebb kérdés: ezen lehetőségek között mennyi egymással nem izomorf gráf van? Ha valakinek van ötlete ezzel kapcsolatban, kérem írja le. Előre is köszönettel: Bertalan Zoltán.
|
|
| [749] marcius8 | 2013-12-20 10:00:36 |
 Tudjuk, hogy ha egy tórusz középkörének sugara "R", meridiánkörének sugara "r", ahol "r" kisebb "R" egyenlőtlenség teljesül (klasszikus úszógumi), akkor a tórusz felszíne 4*pi*pi*R*r és a tórusz térfogata 2*pi*pi*R*r*r. Azt is tudjuk, hogy a pozitív egész számok négyzetének reciprokösszege pi*pi/6. Vajon ez utóbbi állítást nem lehetséges bebizonyítani a tórusz felszínképletének vagy térfogatképletének felhasználásával, tekintettel arra, hogy a "pi*pi" mennyiség itt is és ott is megjelenik? Ha valakinek van ötlete, és megírja, nagyon megköszönöm. Tisztelettel: Bertalan Zoltán.
|
|
|
|
|
| [745] Cogito | 2013-12-09 00:40:38 |
 Egyetértek, a "2. megoldásbeli" azonosság önmagában tényleg bosszantóan kevés.
Az interneten itt olvashatjuk a The Interesting Around Technical Analysis Three Variable Inequalities - Nguyen Duy Tung, Zhou Yuan Zhe.pdf-et, melynek 10-11. oldalán közlik a feladat egy - még mindig nem teljes és sajnos (sajtó)hibás - megoldását. E hibás helyeket negatívba fordítottam. Ide írom a javításukat:
A fekete hátterű részeknél: az egyenlőtlenség helyesen a b b c, a 2-esek helyére pedig 1-esek írandók. c, a 2-esek helyére pedig 1-esek írandók.
Kiegészítésül egy azonosság, amit itt érdemes ismerni: a3b + b3c + c3a - (ab3 + bc3 + ca3) = (a + b + c)(a - c)(c - b)(b - a).
|
 |
| Előzmény: [741] w, 2013-12-02 20:58:17 |
|









 ,z):=(11-6z)
,z):=(11-6z)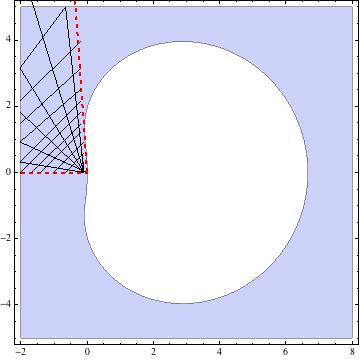

 2, és ez elég is a párossághoz. Címkézetlen csúcsokon vagyunk, így lényegében n pont partíciónak a száma a kérdés, ahol minden egyes részhalmaz legalább 2 elemet tartalmaz. Ennek a generátorfüggvénye meg:
2, és ez elég is a párossághoz. Címkézetlen csúcsokon vagyunk, így lényegében n pont partíciónak a száma a kérdés, ahol minden egyes részhalmaz legalább 2 elemet tartalmaz. Ennek a generátorfüggvénye meg:  1+x2+x3+2x4+2x5+4x6+4x7+7x8+8x9+12x10+14x11+21x12+24x13+34x14+41x15+55x16+66x17+88x18+105x19+137x20+O[x]21
1+x2+x3+2x4+2x5+4x6+4x7+7x8+8x9+12x10+14x11+21x12+24x13+34x14+41x15+55x16+66x17+88x18+105x19+137x20+O[x]21 b
b

