|
| [779] Lóczi Lajos | 2015-10-17 16:56:21 |
 Nagyon érdekes, amit írsz. Tudok egy szerzőpárosról, akiket érdekelne egy ilyen típusú bizonyítás (legalábbis pár éve foglalkoztak ezzel). Fel tudnád velem venni email-ben a kapcsolatot (mivel én nem látom a te címed)?
|
| Előzmény: [778] Róbert Gida, 2015-10-16 21:55:36 |
|
| [778] Róbert Gida | 2015-10-16 21:55:36 |
 Igaz, sőt sokkal több igaz:
&tex;\displaystyle cos(2\Pi n\sqrt 2)+1-\frac{0.13}{n^2}\ge 0&xet; (itt a 0.13 javítható még, de ez az egyenlőtlenség adja a pontos nagyságrendet: 0.16-ra már végtelen sok ellenpélda van).
|
| Előzmény: [777] Lóczi Lajos, 2015-10-16 00:14:23 |
|
| [777] Lóczi Lajos | 2015-10-16 00:14:23 |
 Vajon igaz-e, hogy
&tex;\displaystyle 1+\left(-1/2\right)^n+\cos \left(2 \pi n\sqrt{2} \right)\ge 0&xet;
tetszőleges &tex;\displaystyle n\ge 2&xet; egész szám esetén?
|
|
| [776] Sinobi | 2014-08-16 00:27:42 |
 "Bizonyitsd be, hogy egy erintkezo kor es derekszogu hiperbola eseten 0,2 vagy 4 egyenes lehetseges, amely atmegy az erintesi pontokon, es ugyananolyan hosszu hurt metsz ki mindkettobol!"
Ha adottak A, B es O pontok, akkor az olyan P pontok mertani helye, amelyekre APB szogfelezoje atmegy O-n egy inverz derekszogu hiperbola. Erre a mertani helyre peldaul igaz az, hogy ha egy tetszoleges Q pontjabol ket erintot huzunk sajat magahoz, akkor a ket erinto szogfelezoje atmegy az O ponton.
Ennek az allitasnak egy (gyengitett) inverz valtozata, hogy ha egy kor ket helyen erint egy derekszogu hiperbolat, akkor az egyikre ratukrozve a tukorkep kor is ket helyen erinti.
-------
Egy masik megoldas arra, hogy ket erintkezo kupszelethez maximum 4 ilyen egyenes letezik: huzzunk az erintesi pontbol szeloket! Konjugaljuk a szelo kupszeletekkel vett metszespontjaira az erintesi pontot. Akkor kapunk olyan egyenest, amely egyenhosszu szakaszokat metsz ki a ket erintkezo kupszeletbol, ha az erintesi pont konjugalt kepe vagy metszi az egyik kupszeletet, vagy egy idealis pontban van. Konnyu latni, hogy a konjugalt kep mertani helye egy kupszelet (amely erinti a ket gorbet az erintesi pontjaikban), amely tehat ket pontban metszheti a kupszeletet, es me'g kettoben az idealis egyenest.
Ez nem egyszerubb, de gyokeresen mas megoldas. Van-e me'g?
|
 |
| Előzmény: [775] Sinobi, 2014-08-09 18:15:19 |
|
| [775] Sinobi | 2014-08-09 18:15:19 |
 "(a ket ellipszis kozos pontjait, es az egyik es a masik tukorkepenek kozos pontjait)"
Bizonyitsd be, hogy egy erintkezo kor es derekszogu hiperbola eseten 0,2 vagy 4 egyenes lehetseges, amely atmegy az erintesi pontokon, es ugyananolyan hosszu hurt metsz ki mindkettobol!
|
| Előzmény: [770] Sinobi, 2014-08-06 18:53:46 |
|
|
|
|
| [771] HoA | 2014-08-07 15:39:22 |
 Pedig én is erre látom a megoldás útját. Középpontos tükrözés után oda vezettük vissza a feladatot, hogy "ha két - nem azonos - érintkező ellipszis metszi egymást, akkor pontosan két metszéspont van."
Persze gondolkodom más megoldáson is.
|
 |
| Előzmény: [770] Sinobi, 2014-08-06 18:53:46 |
|
|
|
| [768] Sinobi | 2014-08-05 23:34:03 |
 * ha lezezik 3 ilyen egyenes, akkor vegtelen sok van.
|
|
| [767] jonas | 2014-08-05 22:52:06 |
 Ezt nem igazán hiszem.
Végy egy tetszőleges ellipszist, és rajta egy pontot. Tükrözd az egyenest erre a pontra, így kapsz egy második ellipszist. A két ellipszis akkor ebben a pontban érinteni fogja egymást. A ponton átmenő majdnem bármely egyenes a két ellipszisből ugyanolyan hosszú szakaszokat metsz ki, hiszen a két szakasz egymás tükörképe a pontra.
|
| Előzmény: [766] Sinobi, 2014-08-05 20:50:01 |
|
| [766] Sinobi | 2014-08-05 20:50:01 |
 Talan egy kicsit tul egyszeru ebbe a temaba, de az elozot se lotte le senki.
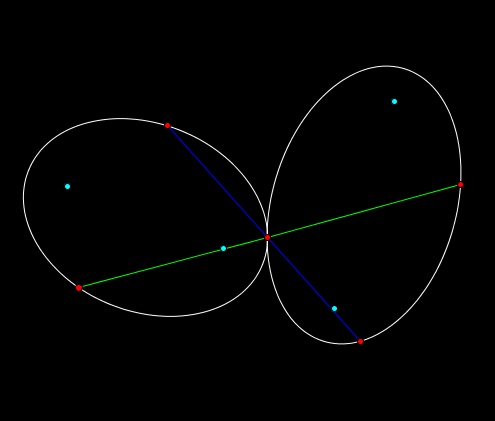
Bizonyitsd be, hogy ket erintkezo ellipszishez (az erinton kivul) maximum ket olyan egyenes letezik az erintesi ponton at, amely ugyanolyan hosszu szakaszokat metsz ki az ellipszisekbol!
abra:
|
 |
| Előzmény: [704] Sinobi, 2013-09-21 18:43:58 |
|
| [765] w | 2014-06-28 15:20:13 |
 És mindez sima De Moivre-képletes játszadozással jön ki (elég az azonosságot &tex;\displaystyle x\in [-1;+1]&xet; esetén belátni, vagyis &tex;\displaystyle x=\cos t&xet; helyettesítéssel). Mint ez vagy ez, csak sokkal egyszerűbb.
|
| Előzmény: [764] Lóczi Lajos, 2014-06-24 22:16:34 |
|
|
| [763] w | 2014-06-24 10:38:44 |
 Legyen &tex;\displaystyle T_n(x)&xet; és &tex;\displaystyle U_n(x)&xet; rendre az &tex;\displaystyle n&xet;-edik elsőfajú és másodfajú Csebisev-polinom. Bizonyítsuk be (vagy cáfoljuk/javítsuk ki, ha esetleg rosszul írtam le) a következő azonosságot:
&tex;\displaystyle 2\sum_{k=1}^n T_k(x)^2=(n-1)+U_n(x)T_n(x)=n+\frac{T_{2n+1}(x)}{2x}.&xet;
|
|
| [762] csábos | 2014-05-21 15:48:02 |
 &tex;\displaystyle (x^2-\frac{1}{2}y^2-\frac{1}{2}z^2-\frac{3}{2}xy+\frac{3}{2}yz)^2 + \frac{3}{4}( y^2-z^2-yz+2zx-xy)^2
= (x^2+y^2+z^2)^2 -3x^3y-3y^3z-3z^3x&xet;
|
| Előzmény: [739] w, 2013-11-29 22:31:58 |
|
| [761] jonas | 2014-02-17 23:18:13 |
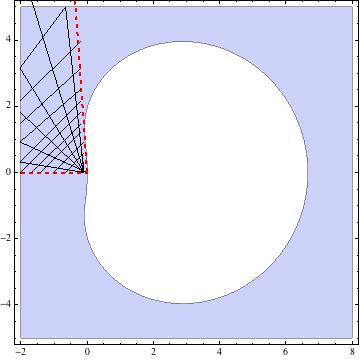
 Az S tartományt algebrai görbe (vagy annak egy része) határolja? Vagyis azon z pontok halmazát keressük, amelyre az f valamelyik gyöke pontosan 1 abszolútértékű. Én azt hiszem, hogy ez egy algebrai görbe, de nem tudom, hogy mennyire könnyű explicit módon fölírni, és hogy hányadfokú lesz.
|
| Előzmény: [760] Lóczi Lajos, 2014-02-17 15:12:07 |
|
|
| [759] marcius8 | 2014-01-24 12:46:40 |
 Még egy újabb kérdés jutott az eszembe, de ez már geometria. Adott három egyforma sugarú és végtelen hosszú henger. A hengerek forgástengelyei páronként egymásra merőlegesek és egy pontban metszik egymást. Tekintsük azt a testet, amely egyenlő a három henger közös részével (metszetével). Mekkora ennek a testnek a felszíne és a térfogata?
|
|
| [758] marcius8 | 2014-01-24 12:42:16 |
 Egy újabb kérdés jutott az eszembe.
A.) Aprajafalván a toronyóra mutatói (kismutató és nagymutató) cm-ben mérve egész számok. 3 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. 2 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. Mekkora lehet a két mutató hossza?
B.) Aprajafalván a toronyóra mutatói (kismutató és nagymutató) cm-ben mérve egész számok. 3 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. 4 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. Mekkora lehet a két mutató hossza?
Ráadásként:
C.) Aprajafalván a toronyóra mutatói (kismutató és nagymutató) cm-ben mérve egész számok. 2 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. 4 óra időtájban a két mutató végpontjának távolsága cm-ben mérve szintén egész szám. Mekkora lehet a két mutató hossza?
Ha valakinek van ezeknek a kérdéseknek a megoldásához ötlete, azt előre is köszönöm. Bertalan Zoltán.
|
|
| [757] aaaa | 2014-01-23 20:36:23 |
 Legyen E(X) a keresett várható érték, és keressük a k fej egymás utáni dobásának várható értékét. Ezt megfeltételezzük (feltételes várható érték tulajdonságai miatt ez menni fog), mégpedig az alapján, hogy az első írásig hány fejet dobunk. Ekkor teljesül
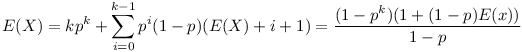
(Az összeget deriválást alkalmazó trükkel lehet könnyen számolni) Ezt kell megoldani E(X)-re, ekkor kapjuk, hogy
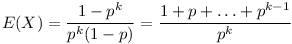
|
| Előzmény: [756] Liklihood, 2014-01-16 13:41:28 |
|
| [756] Liklihood | 2014-01-16 13:41:28 |
 A következő feladat megoldásában kérném a segítségeteket. Legyen egy cinkelt pénzérménk, melyre P(fej)=p=1-P(írás), ahol 0<p<1. Várhatóan hanyadik dobásra következik be, hogy 5 fejet dobunk egymás után?
Válaszaitokat előre is köszönöm. :)
|
|













 ,z):=(11-6z)
,z):=(11-6z)