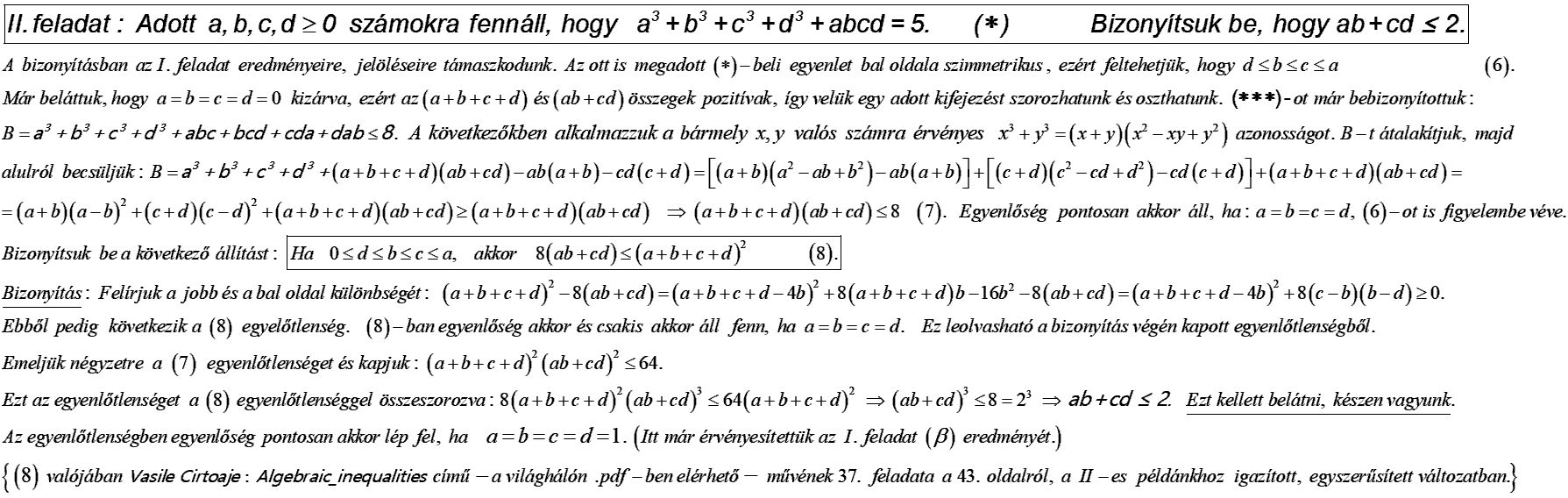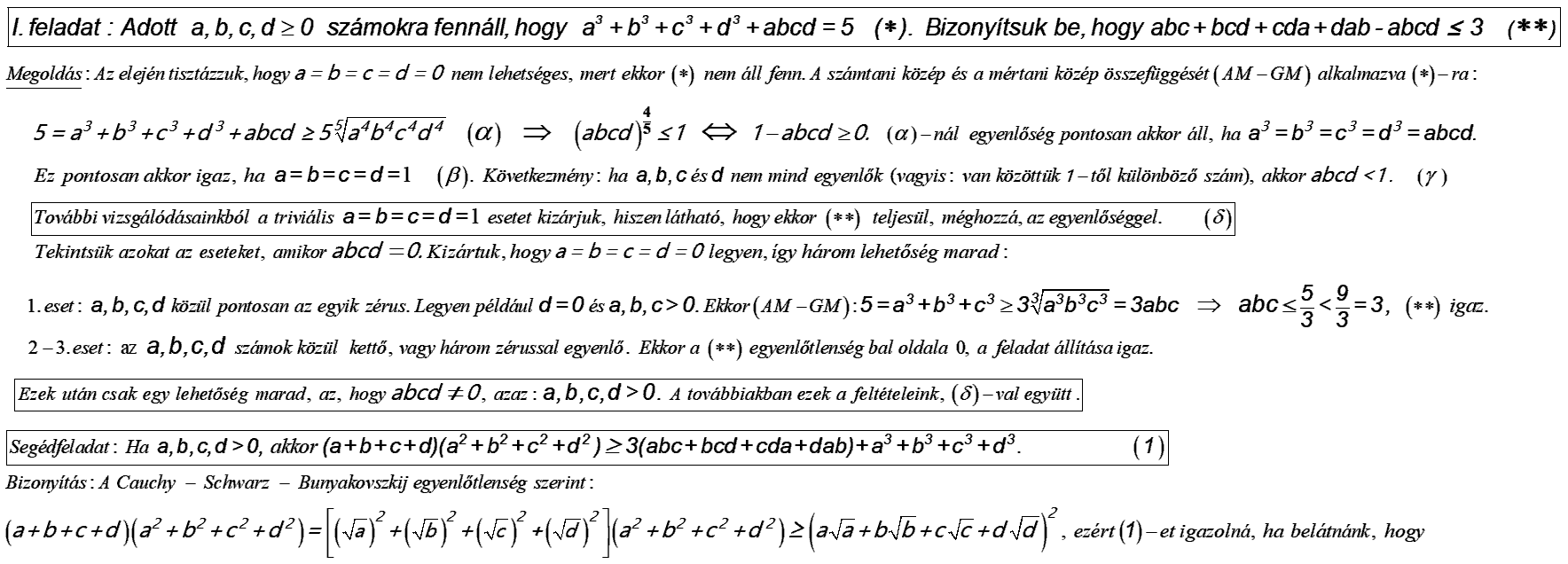(Javított és újratördelt változat.)
A [833]-as hozzászólásban megismert két feladat után következzék a Berkó Erzsébet által felfedezett, kapcsolódó, III. probléma megoldása – középiskolás módszerekkel.
III. feladat: Adott \(\displaystyle a, b, c, d\ge0\) számokra fennáll, hogy \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd=5\) \(\displaystyle (\ast).\)
Bizonyítsuk be, hogy \(\displaystyle a+b+c+d\le4\).
Megoldás: A \(\displaystyle (\ast)\) egyenlet bal oldala szimmetrikus, ezért feltehetjük, hogy \(\displaystyle d\le{b}\le{c}\le{a}\).
Tegyük fel, hogy: \(\displaystyle {a}>{\root 3\of {5}}\). Ekkor \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd>5\), ami ellentmond \(\displaystyle (\ast)\)-nak. Most tegyük fel, hogy \(\displaystyle a<1\). Ekkor \(\displaystyle d^{3},b^{3},c^{3},a^3,abcd<1\) következtében \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd<5\) adódna, ami szintén ellentmondás \(\displaystyle (\ast)\)-ra nézve. Beláttuk tehát, hogy \(\displaystyle 1\le{a}\le{\root 3\of {5}}\). A \(\displaystyle {\bf (*)}\) feltételből az is következik, hogy \(\displaystyle {a}={\root 3\of {5}}\) akkor és csakis akkor igaz, ha \(\displaystyle d=b=c=0\).
Nem állhat fenn \(\displaystyle d>1\) sem: ha \(\displaystyle d>1\) lenne, akkor \(\displaystyle d^{3},b^{3},c^{3},a^3,abcd>1\) következne, ez pedig az \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd>5\) ellentmondáshoz vezetne. Ezzel igazoltuk, hogy \(\displaystyle 0\le{d}\le{1}\). Az eddigiek ismeretében vizsgáljuk meg, hol tartózkodhat az 1-es szám az \(\displaystyle a,b,c,d\) számok sorrendjéhez viszonyítva. Nem lehet \(\displaystyle d>1\) és nem lehet \(\displaystyle a<1,\) ezért csak e három eset fordulhat elő:
\(\displaystyle 1): 0\le{d}\le{1}\le{b}\le{c}\le{a}\)
2): \(\displaystyle 0\le{d}\le{b}\le{1}\le{c}\le{a}\)
3): \(\displaystyle 0\le{d}\le{b}\le{c}\le{1}\le{a}.\)
Mindhárom elrendezésben legyen \(\displaystyle T=4-(a+b+c+d).\) Be kell bizonyítani, hogy \(\displaystyle T\ge0.\)
1) eset: \(\displaystyle 0\le{d}\le{1}\le{b}\le{c}\le{a}.\) Alkalmazzuk a következő helyettesítéseket:
\(\displaystyle d=1-x,b=y+1,c=v+1,a=z+1,\) ahol \(\displaystyle 0\le{x}\le{1}\) és \(\displaystyle y,v,z\ge0\).
A behelyettesítések után a bizonyítandó \(\displaystyle T\ge0\) egyenlőtlenség megfelelője ez lesz: \(\displaystyle T_{1}=x-(y+v+z)\ge0,\) a \(\displaystyle (\ast)\) feltétel pedig így alakul:
\(\displaystyle 0=a^{3}+b^{3}+c^{3}+d^{3}+abcd-5\Longrightarrow\)
\(\displaystyle 0=y^{3}+v^{3}+z^{3}-x^{3}+3(x^{2}+y^{2}+v^{2}+z^{2})+(yvz-xyvz)+(yv-xyv)+\)
\(\displaystyle (vz-vzx)+(yz-xyz)-(xy+xv+xz)+4(y+v+z-x)=\)
\(\displaystyle 4(y+v+z-x)-x(y+v+z)+(1-x)[yvz+yv+vz+zy]+y^{3}+v^{3}+z^{3}+\)
\(\displaystyle [x^{2}-x^{3}]+2x^{2}+3(y^{2}+v^{2}+z^{2})=4(y+v+z-x)+x^{2}+\)
\(\displaystyle [x^{2}-x(y+v+z)]+(1-x)(yvz+yv+vz+zy)+x^{2}(1-x)+y^{3}+v^{3}+z^{3}+\)
\(\displaystyle 3(y^{2}+v^{2}+z^{2})\Leftrightarrow\\
4[x-(y+v+z)]-x[x-(y+v+z)]=\)
\(\displaystyle (1-x)(x^{2}+yvz+yv+vz+zy)+x^{2}+y^{3}+v^{3}+z^{3}+3(y^{2}+v^{2}+z^{2})\Leftrightarrow\)
\(\displaystyle (4-x)[x-(y+v+z)]=(1-x)(x^{2}+yvz+yv+vz+zy)+x^{2}+y^{3}+v^{3}+\)
\(\displaystyle z^{3}+3(y^{2}+v^{2}+z^{2})\; {(**)}.\)
Mivel \(\displaystyle x,y,v,z\ge0\) és \(\displaystyle 4-x>1-x=d\ge{0},\) következik, hogy az utóbbi, \(\displaystyle {\bf(**)}\) egyenlet jobb oldalán nemnegatív kifejezés áll. Ez azt jelenti, hogy a bal oldalán is nemnegatív kifejezésnek kell állnia. Mindent összevetve adódik, hogy \(\displaystyle T_{1}=x-(y+v+z)\ge0,\) amit bizonyítani kellett.
2) eset: \(\displaystyle 0\le{d}\le{b}\le{1}\le{c}\le{a}.\) Alkalmazzuk a következő helyettesítéseket:
\(\displaystyle d=1-x,b=1-y,c=v+1,a=z+1,\) ahol \(\displaystyle 0\le{x,y}\le{1}\) és \(\displaystyle v,z\ge0\).
A behelyettesítések után a bizonyítandó \(\displaystyle T\ge0\)
egyenlőtlenség megfelelője ez lesz: \(\displaystyle T_{2}=x+y-(v+z)\ge0,\) a \(\displaystyle (\ast)\) feltétel pedig így alakul:
\(\displaystyle 0=a^{3}+b^{3}+c^{3}+d^{3}+abcd-5\Longrightarrow\)
\(\displaystyle 0=v^{3}+z^{3}-(x^{3}+y^{3})+3(x^{2}+y^{2}+v^{2}+z^{2})-[v(x+y)+z(x+y)]+\)
\(\displaystyle [2vz-vz(x+y)]-vz+4[v+z-(x+y)]+[xy(v+1)+xyz(v+1)]=\)
\(\displaystyle -(x+y)(v+z)+vz[2-(x+y)]+2[(x-y)^{2}+xy]+[2xy+x^{2}+y^{2}]+\)
\(\displaystyle 4[v+z-(x+y)]+v^{3}+z^{3}-(x^{3}+y^{3})-vz+3[(v-z)^{2}+2vz]+\)
\(\displaystyle xy(v+1)(z+1)\Leftrightarrow4[x+y-(v+z)]=[(x+y)^{2}-(x+y)(v+z)]-\)
\(\displaystyle (x+y)[(x-y)^{2}+xy]+2[(x-y)^{2}+xy]+vz[2-(x+y)]+xy(v+1)(z+1)\)
\(\displaystyle +v^{3}+z^{3}+3(v-z)^{2}+5vz\Leftrightarrow(x+y)[v+z-(x+y)]+4[x+y-(v+z)]=\)
\(\displaystyle [(x-y)^{2}+xy][2-(x+y)]+vz[2-(x+y)]+xy(v+1)(z+1)+v^{3}+z^{3}+\)
\(\displaystyle 3(v-z)^{2}+5vz\Leftrightarrow\)
\(\displaystyle [4-(x+y)][x+y-(v+z)]=[2-(x+y)][(x-y)^{2}+xy+vz]+\)
\(\displaystyle xy(v+1)(z+1)+v^{3}+z^{3}+3(v-z)^{2}+5vz\;(***)\).
Mivel \(\displaystyle x,y,v,z\ge0\) és \(\displaystyle 4-(x+y)>2-(x+y)=(1-x)+(1-y)=d+b\ge{0},\) következik, hogy a \(\displaystyle {\bf(***)}\) egyenletben, az egyenlőségjeltől jobbra nemnegatív kifejezés áll. Ez azt jelenti, hogy a bal oldalon is nemnegatív kifejezést kell találnunk. Mindent összevetve azt kaptuk, hogy \(\displaystyle T_{2}=x+y-(v+z)\ge0.\) Ezt kellett bizonyítani.
3) eset: \(\displaystyle 0\le{d}\le{b}\le{c}\le{1}\le{a}.\) Alkalmazzuk a következő helyettesítéseket:
\(\displaystyle d=1-x,b=1-y,c=1-v,\) ahol \(\displaystyle 0\le{x,y,v}\le{1}.\)
Az 1. esetben a \(\displaystyle {\bf (**)}\) egyenlet bal oldalán a \(\displaystyle T_{1}\) kifejezés szorzója \(\displaystyle P_{1}=4-x.\) A 2. esetben a \(\displaystyle {\bf (***)}\) egyenlet bal oldalán a \(\displaystyle T_{2}\) kifejezés szorzója \(\displaystyle P_{2}=4-(x+y).\) Ezekből megsejthető a képzési szabály, mely szerint a 3. esetben alkalmazható \(\displaystyle P_{3}\) szorzó \(\displaystyle P_{3}=4-(x+y+v)\) lehet. Itt, a 3. esetben a \(\displaystyle P_{3}\) kifejezés \(\displaystyle (b,c,d)\)-változós alakját használjuk:
\(\displaystyle P_{3}=4-(x+y+v)=1+(1-x)+(1-y)+(1-v)={\bf b+c+d+1}.\)
Legyen \(\displaystyle Q=P_{3}T=(b+c+d+1)[4-(a+b+c+d)].\) \(\displaystyle P_{3}>0\) miatt a \(\displaystyle T\ge0\) egyenlőtlenség pontosan akkor teljesül, ha \(\displaystyle Q\ge0.\) Állításunk: \(\displaystyle Q\ge0.\) Indirekt bizonyítással folytatjuk: feltesszük, hogy \(\displaystyle Q<0\), azaz \(\displaystyle Q=(b+c+d+1)[4-(a+b+c+d)]<0 \Leftrightarrow\)
\(\displaystyle 3b+3c+3d-ba-ca-da-b^{2}-2bc-2bd-c^{2}-2cd-d^{2}-a+4<0\)
\(\displaystyle \Leftrightarrow\)
\(\displaystyle 4-a+3(b+c+d)-a(b+b+c)-[b^{2}+c^{2}+d^{2}+2(bc+cd+db)]<0\)
\(\displaystyle \Leftrightarrow\)
\(\displaystyle (b+c+d)^{2}+(a-3)(b+c+d)+a-4>0.\)
Vezessük be az \(\displaystyle s=b+c+d\) új változót, ahol \(\displaystyle 0\le{s}\le{3}\). Ekkor legutóbbi egyenlőtlenségünk az \(\displaystyle s^{2}+(a-3)s+a-4>0\) alakot ölti, ahol az \(\displaystyle a\) paraméterről tudjuk, hogy \(\displaystyle 1\le{a}\le{\root 3\of {5}}\). Rögzítsük az \(\displaystyle a\) paramétert és tekintsük az \(\displaystyle f(s)=s^{2}+(a-3)s+a-4,\) az \(\displaystyle s\) változóra nézve másodfokú függvényt, ahol \(\displaystyle 0\le{s}\le{3},\) továbbá \(\displaystyle 1\le{a}\le{\root 3\of {5}}\approx1,71.\) (A megoldás végén az \(\displaystyle a\) szám az \(\displaystyle [1,\root 3\of {5}]\) intervallumon végigfutva minden olyan értéket felvehet, melyre fennáll a \(\displaystyle (\ast)\) feltétel.)
Indirekt feltevésünk szerint \(\displaystyle f>0,\) ezért az \(\displaystyle f=0\) másodfokú paraméteres egyenlet \(\displaystyle D\) diszkriminánsára teljesülnie kell, hogy \(\displaystyle D<0.\) Ezzel szemben: \(\displaystyle D=(a-3)^{2}-4(a-4)=a^{2}-10a+25=(a-5)^{2}>0\), ami azt jelenti, hogy az \(\displaystyle f=0\) egyenletnek mindig van valós megoldása, s ez ellentmond az indirekt feltevésnek. Ezzel beláttuk, hogy a \(\displaystyle Q<0\) indirekt állítás hamis volt, s ebből következik, hogy a \(\displaystyle Q\ge0\) egyenlőtlenség igaz. Utóbbival ekvivalens, hogy \(\displaystyle T\ge0,\) amit bizonyítani kellett.
Megjegyzések:
Ha a \(\displaystyle {\bf (**)}\) és \(\displaystyle {\bf (***)}\) egyenleteket felírjuk úgy, hogy \(\displaystyle x,y,v,z\) helyére a \(\displaystyle d,b,c,a\) számok alkotta, megfelelő kifejezések kerülnek, akkor – a beszorzások és egyszerűsítések után – rendre megkapjuk a kiindulási \(\displaystyle {\bf (*)}\) feltételt. (Ellenőrzés.)
Van-e valakinek eltérő, középiskolás levezetése? Főleg a 3. eset nem indirekt megoldása érdekelne (ha létezik ilyen egyáltalán).
|