Fórum: Nehezebb matematikai problémák

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34]

Szeretnél hozzászólni? Jelentkezz be.

[100] Kós Géza

2004-10-11 16:49:44

A feladat annak igazolása, hogy az f(x)ⁱg(x)^j alakú polinomok közül kiválasztható néhány, ami lineárisan összefüggő.

Legyen n olyan pozitív egész, ami f és g fokánál is nagyobb. (Azért kell ilyen furcsán fogalmazni, hogy a konstans polinomokból ne lehessen kellemetlenség.)

Tekintsük azokat az fⁱ(x)^.g^j(x) polinomokat, amikre i,j<2n. Ez össesen 4n² darab polinom. Mindegyik foka legfeljebb 2(2n-1)(n-1)<4n²-1. A kiválasztott polinomok tehát többen vannak, mint az általuk kifeszített tér dimenziója...

Előzmény: [99] Sirpi, 2004-10-11 15:37:09

[99] Sirpi

2004-10-11 15:37:09

19. feladat: Adott két valós együtthatós polinom: f(x) és g(x). Bizonyítsuk be, hogy ezekhez mindig létezik olyan h(y,z) kétváltozós, nem az azonosan nulla polinom, melyre h(f(x),g(x)) $\equiv$ 0.

(Saját ötlet, úgy érzem, meg is oldottam, de a megoldásom nem túl szép és vannak benne picit ködös pontok is. Azért tűzöm ki, hátha valaki ad rá egy frappáns megoldást)

[98] Kemény Legény	2004-10-10 20:07:32
A 2. feladatra n=2004+(1002!)² jon ki,ugyanis n-2004 felbomlik 2004 kulonbozo egesz szorzatara $\implies$ n-2004 legalabb (-1002)(-1001)..(-1)(1)..(1001)(1002).(Erre van is polinom, -(x-1002)...(x-1)(x+1)...(x+1002)+2004+(1002!)²),ez x=0-ra 2004,x=-1002,...,-1,1,...1002-re pedig eppen n).
Előzmény: [95] Csimby, 2004-10-10 01:08:18

[97] Csimby	2004-10-10 19:50:37
Hú, de szép! Köszi.

[96] Kemény Legény	2004-10-10 19:22:46
Keves Csimby!A 3. feladatnal a piros sorozatok hosszanak valtakozo elojelu osszegenek a harommal valo oszthatosaga nem valtozik egy lepes soran(ellenorizd le,ha nem hiszed).2 kekre ez 0 oszthato 3-mal,mig 2 pirosrara +-2 nem oszthato 3-mal.Igy nem elerheto. A megoldas nem sajat:Molnar Andristol(11.o.)szarmazik.
Előzmény: [95] Csimby, 2004-10-10 01:08:18

[95] Csimby	2004-10-10 01:08:18
Valami okos ember beírhatná a Kürschák példák megoldásait, szerintem sokan kíváncsiak rá...

[94] nadorp

2004-04-09 07:58:34

Sziasztok !

Gubbubu 12. feladatát [27] ugyan nem oldottam meg ( Péter ellenpéldája alapján nem is igaz), most csak arra szeretnék egy egyszerű példát adni, hogy az álítás milyen messzire vezet(ne).

Legyen q=2^p-1 Mersenne-prím. Ekkor 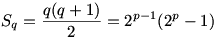$S_q=\frac{q(q+1)}2=2^{p-1}(2^p-1)$ tökéletes szám.Így

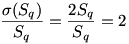$\frac{\sigma(S_q)}{S_q}=\frac{2S_q}{S_q}=2$ , ezért az állításból következne, hogy véges sok Mersenne-prím van.

[93] Gubbubu

2004-04-06 13:50:14

Kedves Pach Péter Pál!

A 12. feladatot én - Gubbubu tűztem ki. Először is nagyon köszönöm, hogy foglalkoztál vele. Másodszor csak annyit mondtam, hogy az állítás "valószínűleg" igaz. A Derive program szerint ugyanis igaz. Jónak tűnik amit írtál - hétvégén, ha hozzájutok, részletesebben is átnézem - úgyhogy a tanulság az: ne bízzunk meg feltétlenül a számítógépes programokban, különösen ha határértékszámításról van szó.

Üdv.: G.

Előzmény: [91] Pach Péter Pál, 2004-04-05 23:05:17

[92] Pach Péter Pál

2004-04-05 23:06:56

Fazekas-pályázat feladatok voltak:

18. feladat

a) Van-e olyan nem konstans folytonos függvény, amelynek minden helyen helyi szélsőértéke van?

b) Van-e olyan függvény, amely pontosan a racionális pontokban folytonos?

(c) Van-e olyan függvény, amely pontosan az irracionális pontokban folytonos? – Csak gyakorlásnak, a másik kettőnél lényegesen könnyebb.)

[91] Pach Péter Pál

2004-04-05 23:05:17

Szerintem a 10. feladat [24] mindhárom kérdésére nemleges a válasz.

A. Legyen n $\in$ N. Ha A(n)={x:f(x)=n} nem megszámlálható számosságú, akkor A(n)-re a feltétel nem teljesül.

$\forall$ n:A(n) megszámlálható $\implies$ ÉT is megszámlálható, ellentmondás

B. Most még egy feltétel van, de már A-hoz sincs megfelelő függvény.

C. Legyen y $\in$ R. Ha A(y)={x:f(x)=y} nem megszámlálható, akkor A(y)-ra nem teljesül a feltétel. Ha A(y) megszámlálható (vagy véges), akkor R\A(y)-ra nem teljesül a feltétel, ellentmondás.

A 12. feladatot [27] is nehezen tudom értelmezni, valamit nagyon elnézhetek benne. Legyen pl. n=2k, ekkor S_n=k(2k+1).

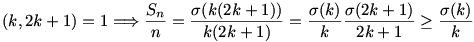
$(k,2k+1)=1 \implies \frac{S_n}{n}=\frac{\sigma(k(2k+1))}{k(2k+1)}=\frac{\sigma(k)}{k}\frac{\sigma(2k+1)}{2k+1}\ge\frac{\sigma(k)}{k}$

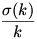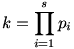Válasszuk meg úgy k-t, hogy $\frac{\sigma(k)}{k}$ „jó nagy” legyen: $k=\prod_{i=1}^s{p_i}$ , ahol p_i-k a prímszámok.

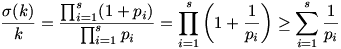
$\frac{\sigma(k)}{k}=\frac{\prod_{i=1}^s(1+p_i)}{\prod_{i=1}^s{p_i}}=\prod_{i=1}^s{\left(1+\frac{1}{p_i}\right)}\ge \sum_{i=1}^s{ \frac{1}{p_i}}$

Ismert, hogy ha s-et elég nagynak választjuk, akkor pl. 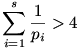$\sum_{i=1}^s{ \frac{1}{p_i}}>4$ . Ebből már következik, hogy a feladat állítása nem igaz.

[90] Sirpi

2004-03-25 10:25:44

Sziasztok!

Elnézést a hosszú szünetért, de pár dolog közbejött...

Most viszont mutatok egy konstrukciót arra, hogy minden n, m pozitív egészre meg lehet adni úgy m+n-d-1 számot, hogy bármely egymás utáni n összege pozitív, bármely egymás utáni m összege pedig negatív legyen.

Ezt elég relatív prímekre bizonyítani, mert ha n=dn', m=dm', és (n',m')=1, valamint az n',m' párra van n'+m'-2 hosszú megoldás, akkor ezt 0-kkal felhigítva: az első szám elé, az utolsó mögé, és minden két szám közé is d-1 nullát beiktatva, (n'+m'-2)+(d-1)(n'+m'-1)=d(n'+m'-1)-1=n+m-d-1 hosszú sorozatot kapunk, és könnyű látni, hogy ez az n,m párra jó megoldást ad.

Innentől kezdve tehát feltehető, hogy n és m relatív prím, ilyenkor n+m-2 a konstruálandó hossz. Ha valamelyik szám, például m=1, akkor könnyű a dolgunk, mert ekkor n-1 hosszú sorozat kell, a csupa-(-1) megfelel a célnak. Tegyük fel ezért, hogy n,m $\geq$ 2.

Az eredeti állítás helyett azt fogom bizonyítani, hogy ki lehet az első m+n-2 számot két színnel (pirossal és kékkel) színezni úgy, hogy bármely szomszédos n szám között ugyanannyi (0<c<n) piros legyen, és bármely m szomszédos között ugyanannyi (0<d<m) piros legyen. Ugyanis ha ez sikerül, akkor a piros számokba P-t, a kékekbe K-t írunk értékként úgy, hogy cP+(n-c)K>0 és dP+(m-d)K<0 teljesüljön.

Ha n és m relatív prím, akkor ennek mindig van egész megoldása, például vesszük a cP+(n-c)K=1 és dP+(m-d)K=-1 lineáris egyenleteket (P-re és K-ra), relatív prím esetben ennek egyértelmű a megoldása, sőt racionális. A megoldásként kapott P és K nevezőjének legkisebb közös többszörösével megszorozva a számokat, egész megoldást kapunk.

Most már csak a tényleges konstrukció van hátra. Az alapötlet az euklídeszi algoritmus.

Legyen n>m és tegyük fel, hogy szeretnénk n+m-2 hosszú piros-kék színezést. Ha lenne n-m,m-re (n-m)+m-2 hosszú jó színezésünk, akkor állítom, annak az utolsó m elemét még 1x a színezett számok után rakva jó színezést kapnánk.

Legyen az n-m,m párra bármely szomszédos n-m között c piros, és bármely m között d piros (0<c<n-m, 0<d<m). Ekkor a kibővített sorozatban is bármely egymás utáni m között c piros lesz, és bármely egymás utáni n=(n-m)+m között pedig c+d. Ezeket könnyű látni, ha nem baj, akkor nem megyek bele részletesen.

Ezzel a módszerrel a feladatot mindig kisebb és kisebb számokra kell megoldani, kérdés, hogy mikor állunk le. Előbb-utóbb eljutunk az 1,k párhoz valamilyen k-ra, de ne itt álljunk meg, hanem 1 lépéssel előbb. A legelső 1,k pár előtt csak k+1,k lehetett az előző számpár. Erre pedig könnyen megy a konstukció, mert k+(k+1)-2=2k-1 hossz kell. Ha most a középső elemet pirosra színezzük, a többit meg kékre, akkor c=1 és d=1 lesz könnyen látható módon, tehát a színezés megfelel a feltételeknek.

Ennyi a bizonyítás dióhéjban, remélem, nem volt túl hosszú, és nem voltam túl szűkszavú bizonyos helyeken, de ha bárkinek van kérdése, akkor nyugodtan kérdezzen. Ja, és bocs, hogy ennyit kellett várni :-)

Sirpi

[89] Sirpi

2004-02-27 13:29:15

Szia Nadorp!

Köszi a megoldást, teljesen jó. Amúgy ez az alapötlete az én konstrukciómnak is, amit mondjuk hétfőn beírok, ha addig nem csap le rá senki (hétvégén síelek :-) ).

Előzmény: [88] nadorp, 2004-02-27 10:47:48

[88] nadorp

2004-02-27 10:47:48

Felső korlát megadása Sirpi [75] feladatára.

Legyenek m,n pozitív egészek és legyen (m,n)=d. Ekkor legfeljeb m+n-d-1 darab valós szám adható meg úgy, hogy közülük bármely szomszédos n darab összege pozitív és bármely szomszédos m darab összege negatív.

Tegyük fel, hogy az állítással ellentétben létezik m+n-d darab, a feltételeknek megfelelő szám. Legyenek ezek x₁,x₂,...x_n+m-d.Előrebocsátunk két nyilvánvaló észrevételt:

1, Ha létezik a feltételeknek megfelelő sorozat, akkor olyan is létezik,amelyben bármely n darab szomszédos összege negatív és bármely m darab szomszédos összege pozitív ui. csak minden elemet meg kell szorozni -1-gyel.

2, n nem osztója m-nek és viszont

Az 1. észrevétel miatt feltehető, hogy n<m.Osszuk el m-et maradékosan n-nel:

m=nx₁+r₁ 0<r₁<n, d|r₁

Mivel az első m szám összege negatív, de bármely n szomszédos összege pozitív, ezért

x₁+x₂+...x_r₁<0. Teljesen hasonlóan

x₂+x₂+...x_r₁+1<0

...

x_n-d+1+...x_n+r₁-d<0

Azt kaptuk, hogy létezik n+r₁-d darab szám, hogy közülük bármely r₁ szomszédos összege negatív és bármely szomszédos n összege pozitív, de ekkor az 1.észrevétel miatt létezik n+r₁-d darab szám, hogy közülük bármely r₁ szomszédos összege pozitív és bármely szomszédos n összege negatív.

A fenti gondolatmenetet most a r₁,n számokra alkalmazva,ha

n=r₁x₂+r₂ 0<r₂<r₁, d|r₂

akkor létezik r₁+r₂-d darab szám, hogy közülük bármely r₂ szomszédos összege pozitív és bármely szomszédos r₁ összege negatív.

A fenti folyamat vég nélkül nem folytatható, ezért lesz egy olyan k index, hogy

r_k-1=r_kx_k+1+r_k+1 0<r_k+1<r_k, d|r_k+1

r_k=r_k+1x_k+2+d

és létezik r_k+1+d-d=r_k+1 darab szám, hogy bármely szomszédos d összege pozitív és az r_k+1 összege negatív. Ez viszont a 2. észrevétel miatt ellentmondás.

[87] nadorp	2004-02-26 15:28:01
Teljesen jó.
Előzmény: [86] Sirpi, 2004-02-26 14:48:53

[86] Sirpi

2004-02-26 14:48:53

Ha bonyi a bizonyításod egy része, akkor írd le csak a felső becslése(i)d bizonyítását. Amit én adtam megoldást a felső korlát élességére, az konstruktív, és aránylag egyszerű, ha nem lesz más megoldó, akkor azt a részt beírom én. Jó lesz így?

Sirpi

Előzmény: [85] nadorp, 2004-02-26 14:43:47

[85] nadorp

2004-02-26 14:43:47

Szia Sirpi !

Kösz a segítséget, így már könnyebb volt (0...0). Én is próbálkoztam a relatív prím megoldásba "beszúrkálni", csak az volt a baj, hogy két elem közé d darab elemet és a maradék d-1 elemet meg valahogy elosztogatni.

A megoldást nem tudom, érdemes-e közölni, mert szerintem egy picit hosszú a fórumhoz. A másik baj az vele, hogy relatív prímekre felhasználtam egy kis lineáris algebrát (rezultáns) és csak egzisztenciát bizonyít, tehát nem konstruktív.

N.P.

Előzmény: [84] Sirpi, 2004-02-26 10:31:48

[84] Sirpi

2004-02-26 10:31:48

Szia nadorp!

Gratulálok, lényegében megoldottad a feladatot! Az n+m-d-1 valóban éles korlát minden n,m-re (a d=1 esetre is jó). Az, hogy a korlát elérhető nem relatív prím esetben, nem olyan nehéz. Legyen (n,m)=d, n=dn', m=dm', és tegyük fel, hogy a relatív prím n',m'-re már van n'+m'-2 hosszú jó sorozatunk.

Ezt kellene "felduzzasztani", pl. bármely két elem közé, sőt, legelőre és leghátulra is d-1 új elemet (de vajon mit?) betenni, ekkor ugyanis n'+m'-2+(n'+m'-1)(d-1)=n'd+m'd+d-1=n+m-d-1 elemű lesz a felduzzasztott sorozat. Remélem, így már összeáll a teljes bizonyítás.

Sirpi

Előzmény: [83] nadorp, 2004-02-26 09:09:55

[83] nadorp

2004-02-26 09:09:55

Szia Sirpi !

Az általad kitűzött példához részeredményein vannak, de egyelőre nem tudom eldönteni, hogy jó helyen kereskedek-e. Jelölje S a maximális elemszámot. Ekkor

1, Ha n=1,m=1, akkor nincs megoldás

2, Ha n|m, akkor S=m-1 ( ugyanez igaz fordítva)

3, Bizonyítottam, hogy S $\le$ n+m-2

4, Bizonyítottam, hogy m és n relatív prímek, akkor S=n+m-2 ( ez a bizonyítás sajnos nem teljesen elemi )

5, Bizonyítottam, hogy ha (m,n)=d és d $\ge$ 2, akkor S<=m+n-d-1

6, Egyelőre még nem látom, hogy az 5-ben levő felső korlát elérhető-e.

Üdv

N.P.

Előzmény: [75] Sirpi, 2004-02-17 08:51:41

[82] Hajba Károly	2004-02-20 00:38:27
Rágódásom egy részeredménye, ha jól értelmeztem a cikket, akkor így néz ki valahogy:

Előzmény: [81] Hajba Károly, 2004-02-19 23:26:36

[81] Hajba Károly

2004-02-19 23:26:36

Kedves László!

Megkaptam a drótpostát, a kutatásért ezer köszönet, mind Neked, mind a többieknek. Már én is rágódom rajta.

Előzmény: [80] lorantfy, 2004-02-19 21:14:48

[80] lorantfy

2004-02-19 21:14:48

Kedves Géza és Erdős-Graham Érdeklődők!

Ma voltam bent a Rényi Intézetben és már meg is van a cikk, most scanneltem és már tudom is küldeni minden érdeklődőnek. 5 oldal (persze angolul) 1 Mega. Nagyon érdekes én most "rágcsálom".

Előzmény: [79] Kós Géza, 2004-02-19 20:50:28

[79] Kós Géza

2004-02-19 20:50:28

Kicsit keresgéltem a citeseeren, és a következőt találtam:

P. Erdős and R. L. Graham. On packing squares with equal squares. J. Comb. Theory (A), 19, 1975, 119-123.

Keresd a "Journal of Combinatorial Theory, Series A" című lapot a Rényi Intézetben.

Előzmény: [78] Kós Géza, 2004-02-19 20:33:42

[78] Kós Géza

2004-02-19 20:33:42

Kedves gubbubu,

Próbálkozhatsz a Rényi Intézet könyvtárával (Reáltanoda utca, a Ferenciek tere és az Astoria között) is. Személyes tapasztalataim szerint az a legbővebb.

Előzmény: [77] Gubbubu, 2004-02-19 20:26:14

[77] Gubbubu

2004-02-19 20:26:14

Kedves László, kedves Onogur!

Jókívánságaitokat köszönöm, új erőre kaptam tőlük. Holnap talán eljutok az ELTE matematika könyvtárába (egyszer már próbáltam, kevés sikerrel, de ígérték, hogy utánanéznek bizonyos dolgoknak ez ügyben). Egyszóval annak ellenére, hogy egy matematikusnak talán tényleg több esélye van, én is folytatom a keresést a magam igen szerény eszközeivel.

Üdv:G.

Előzmény: [69] lorantfy, 2004-02-12 07:46:02

[76] Kiss Demeter

2004-02-17 21:44:37

Sziasztok!

Megtetszett a másodfokú polinomos példa és írtam egy programot, mely lorantfy jelölését használva a c,d,e,f,g és b számokat keresi meg. (Azaz a másodfokú polinom x=0,1,2,3,4 helyeken felvett értekeinek pozitív négyzetgyökeit).

Sajnos még nem talált a feladat állításának megfelelő számötöst, de találtam néhány számnégyest:(az i. oszlopban lévő szám az i-1 helyen felvett érték pozitív négyzetgyöke, továbbá az utolsó szám a b értéke):

6, 23, 32, 39, 246

39, 70, 91, 108, 1689

108, 157, 194, 225, 6492

225, 296, 353, 402, 18495

16, 87, 122, 149, 3656

402, 499, 580, 651, 43698

51, 148, 203, 246, 9651

651, 778, 887, 984, 90741

147, 302, 401, 480, 34797

984, 1145, 1286, 1413, 171384

79, 242, 333, 404, 26161

59, 228, 317, 386, 24251

1413, 1612, 1789, 1950, 300987

324, 557, 718, 849, 102636

1950, 2191, 2408, 2607, 498990

2607, 2894, 3155, 3396, 789393

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34]

Már regisztráltál?
Új vendég vagy?