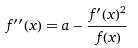| [680] Maga Péter | 2013-04-12 18:06:20 |
 Először röviden vázolom, hogy bizonyítja be az ember, hogy a szabályos 11-szög nem szerkeszthető. Miből áll a szerkesztés egy lépése? Általában véve sokféle lehet, de pontot csak háromféleképp kaphatsz: veheted már meglévő két egyenes, két kör vagy egy egyenes és egy kör metszéspontját (már meglévő egyenes: két pontja ismert, már meglévő kör: középpontja és egy kerületi pontja ismert). Most pakoljunk be mindent koordináta rendszerbe, kezdetben adottak mondjuk a (0,0) és (1,0) pontok. Ezek után mindig, amikor új pontot kapunk, annak mindkét koordinátája kifejezhető racionális számokból az alapműveletek és négyzetgyökvonás segítségével. Ezt indukcióval könnyű bebizonyítani: ilyen pontokra illeszkedő egyenesek metszéspontja ilyen stb.
Valójában áttérhetünk pontok szerkesztéséről számok szerkesztésére. Egy szabályos 11-szög szerkesztése ekvivalens a cos (2k /11) (vagy sin (2k/ /11) (vagy sin (2k/ /11) számok) szerkesztésével k=1,...,10-re. Ezek a számok viszont nem kaphatók meg a racionális számokból pusztán alapműveletekkel és négyzetgyökvonással. /11) számok) szerkesztésével k=1,...,10-re. Ezek a számok viszont nem kaphatók meg a racionális számokból pusztán alapműveletekkel és négyzetgyökvonással.
Van az algebrában egy olyan fogalom, hogy test. Ez egy olyan halmaz, amin összeadást, kivonást, szorzást, osztást tudsz végezni a szokásos műveleti tulajdonságokkal (tagok felcserélhetősége, csoportosíthatósága, zárójelfelbontás). A racionális számok például testet alkotnak. Hasonló módon testet alkotnak az 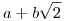 alakú (a,b racionálisok) számok is, ez a test tartalmazza Q-t. Ehhez hasonló esetekben lehet arról beszélni, hogy egy test egy másik felett hányadfokú. Ez lényegében az, hogy veszel egy olyan alakú (a,b racionálisok) számok is, ez a test tartalmazza Q-t. Ehhez hasonló esetekben lehet arról beszélni, hogy egy test egy másik felett hányadfokú. Ez lényegében az, hogy veszel egy olyan  elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a 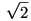 ilyen: ha hozzáveszed Q-hoz, utána már minden más előáll az alapműveletekkel), és kiszámolod, legalább hányadfokú F1-beli együtthatós polinomnak a gyöke ilyen: ha hozzáveszed Q-hoz, utána már minden más előáll az alapműveletekkel), és kiszámolod, legalább hányadfokú F1-beli együtthatós polinomnak a gyöke  . A konkrét példában: . A konkrét példában: 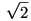 nem gyöke egyetlen Q együtthatós elsőfokú polinomnak sem (hiszen irracionális), de másodfokúnak már igen: x2-2 (az ilyen legkisebb fokú polinomot hívjuk minimálpolinomnak). Tehát a konkrét példában ez a fok 2. A szerkesztendő számok nyelvén mindig ilyen történik: ha az eddig megszerkesztett számok benne vannak egy F1 testben, akkor a következő megszerkesztett szám benne lesz egy olyan F2 testben, ami vagy maga F1 (nincs bővítés), vagy pedig F1 egy másodfokú bővítése. Bővítés bővítése esetén a fokszámok összeszorzódnak. Így ha sokszor bővítünk, akkor is mindig olyan számaink lesznek csak, amiknek a Q feletti minimálpolinomjának foka 2-hatvány. Viszont cos (2 nem gyöke egyetlen Q együtthatós elsőfokú polinomnak sem (hiszen irracionális), de másodfokúnak már igen: x2-2 (az ilyen legkisebb fokú polinomot hívjuk minimálpolinomnak). Tehát a konkrét példában ez a fok 2. A szerkesztendő számok nyelvén mindig ilyen történik: ha az eddig megszerkesztett számok benne vannak egy F1 testben, akkor a következő megszerkesztett szám benne lesz egy olyan F2 testben, ami vagy maga F1 (nincs bővítés), vagy pedig F1 egy másodfokú bővítése. Bővítés bővítése esetén a fokszámok összeszorzódnak. Így ha sokszor bővítünk, akkor is mindig olyan számaink lesznek csak, amiknek a Q feletti minimálpolinomjának foka 2-hatvány. Viszont cos (2 /11)+isin (2 /11)+isin (2 /11) minimálpolinomja x10+x9+...+x+1, ami tizedfokú. /11) minimálpolinomja x10+x9+...+x+1, ami tizedfokú.
Általában is ez a procedúra. A szabályos n-szög szerkeszthetősége visszamegy az n. körosztási polinomra: ez az xn-1 egyik tényezője, a cos (2 /n)+isin (2 /n)+isin (2 /n) minimálpolinomja. Ennek foka pedig /n) minimálpolinomja. Ennek foka pedig  (n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk. (n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk.
Ezek mély dolgok. Majd tanulod:).
(Ez csak egy sebtében írt vázlat, de ha valamit elírtam, majd valaki kijavít.)
|
| Előzmény: [678] w, 2013-04-12 17:03:12 |
|
|
|
|
|
| [675] marcius8 | 2013-04-12 12:52:40 |
 Nagyon hálás lennék annak, aki a következő összefüggések bármelyikét bizonyítani tudja. Ezeket az összefüggéseket én csak megsejtettem, ugyanis mindenképpen egy szabályos 11 oldalú (!) sokszöget akartam szerkeszteni.
|
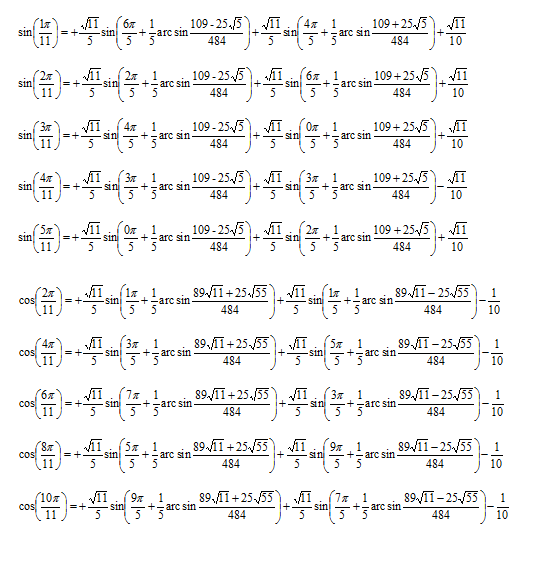 |
|
| [674] w | 2013-04-08 16:38:02 |
 Na szóval,
1. Mennyi a négyzetszámok lehetséges maradéka 3-mal osztva (kérlek, használd fel, amit írtam korábban, és írd le a megoldást ide)?
2. Miért nincs négyzetszám a következő számok között: 11, 101, 1001, ... ? (Segítség: vajon mennyi lesz a 3-as maradékuk?).
|
| Előzmény: [673] nyerek01, 2013-04-08 02:04:18 |
|
|
| [672] w | 2013-04-06 20:31:46 |
 Kis lökés rajta: először keressük meg a legfeljebb n-edfokúakat. Igazoljuk, hogy pontosan egy van. Konstruáljuk is meg azt. Az általános eset ennél nehezebb, azt még nem oldottam meg.
(Ez ismert feladat. A hozzáértők kérem, ne lőjék le.)
|
| Előzmény: [669] w, 2013-04-01 20:26:25 |
|
| [671] w | 2013-04-06 20:11:54 |
 Ez nem nehéz feladat. Osszuk el az n számot maradékosan 3-mal: n=3k+r (n, k egész szám; r lehet 0, 1 vagy 2). Ekkor mennyi lesz n2? Ebből megállapítható n2 3-as maradéka. Meglepő eredmény.
Próbáld megoldani akkor a következő feladatot. Hány négyzetszám van a következő számok között: 1, 11, 101, 1001, 10001, ...?
|
| Előzmény: [670] nyerek01, 2013-04-06 17:09:12 |
|
| [670] nyerek01 | 2013-04-06 17:09:12 |
 Bizonyítsa hogy: nincs négyzetszám, ami hárommal osztva kettőt ad maradékul (bocs ha rossz helyre írtam, mert kevés az itteni szinthez)
|
|
| [669] w | 2013-04-01 20:26:25 |
 Adottak a páronként különböző x1, x2, ..., xn, illetve a1, a2, ..., an számok. Keressük meg az összes olyan P polinomot, melyre P(xi)=ai ( i). i).
|
|
| [668] Hajba Károly | 2013-02-02 23:26:11 |
 Én úgy érzem, ahhoz, hogy érdekessé kezdjen válni, az egyik n-t m-mé kell átírni és elhagyni az egyenlő szárú kitételt. Az egybevágóság meg kötelező kell, hogy legyen, mivel enélkül nincs 'megkötés'.
Ez egyébként a diszkrét matematika parkettázás vagy csempézés részéhez tartozik. Ha kicsit finoman módosítunk a feltételeken, akkor Pakomániába érkezünk.
|
| Előzmény: [667] w, 2013-02-02 15:29:34 |
|
| [667] w | 2013-02-02 15:29:34 |
 Adok okot is arra, hogy felhozzuk. :P. Kiötlöttem egy feladatot, amit tényleg nehéznek találok, és nagyon más témába nem illett bele.
Hányféleképpen darabolható fel egy szabályos n-szög n db egybevágó egyenlő szárú háromszögre? Mi a helyzet, ha valamelyik feltételt elhagyjuk?
|
| Előzmény: [666] Bütyök, 2011-09-18 18:43:43 |
|
| [666] Bütyök | 2011-09-18 18:43:43 |
 Ez egy jó topik. Felhozom:)
|
|
|
| [664] leni536 | 2009-07-11 23:43:51 |
 Ezek szerint nincs se kezdeti sebesség, sem pedig kezdeti hossz. Valami akkor az összeneregiával nem stimmel, mert ha állandó a gyorsulás, akkor a helyzeti energia az idő negyedik hatványával csökken, a mozgási energia viszont az idő második hatványával növekszik, úgyhogy egy kezdeti szakaszon biztos, hogy nem fedezi a mozgási energiát a helyzeti energia változása.
|
| Előzmény: [663] Timár Máté, 2009-07-11 22:57:33 |
|
| [663] Timár Máté | 2009-07-11 22:57:33 |
 nos köszönöm szépen kedves nadorp és Lóczi Lajos! Egyébként a differenciálegyenlet egy Eötvös-versenyfeladatból származik (1997,2.feladat...dióhéjban:egy asztal tetejéről egy L hosszúságú lánc csorog le egy lyukon keresztül,kérdés hogy mennyi idő alatt ér le ennek az eleje és a vége az ugyancsak L-mélyen levő talajra). A megoldókulcsban nem szerepelt megoldás,amolyan "vegyük észre hogy..." módszerrel oldódott meg a feladat .A kötél asztalról lelógó hossza legyen x, sebessége v,gyorsulása a,ekkor:
|
 |
|
|
|
|
| [659] nadorp | 2009-07-06 16:14:21 |
 Csak hogy ne legyen nyúl a kalapból.
Legyen z(y)=y' Ekkor
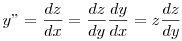 , tehát az egyenlet , tehát az egyenlet
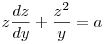
Ez egy elsőrendű,inhomogén differenciál egyenlet z(y)-ra. Innen
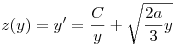
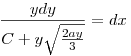
Ez pedig az y=t2 helyettesítéssel kiintegrálható.
Az előző hozzászólás a C=0 eset volt.
|
| Előzmény: [658] nadorp, 2009-07-06 11:24:27 |
|
|
|
| [656] Timár Máté | 2009-06-30 22:02:39 |
 Sziasztok! Valaki segítene az alábbi differenciálegyenlet megoldásában?
|
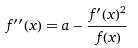 |
|



 /11) (vagy sin (2k/
/11) (vagy sin (2k/ elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a
elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a  (n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk.
(n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk. 

 0 és pi-k páronként különböző Fermat-prímek, tehát olyan alakú prímek, mint amit te is írtál: 22r+1.
0 és pi-k páronként különböző Fermat-prímek, tehát olyan alakú prímek, mint amit te is írtál: 22r+1.
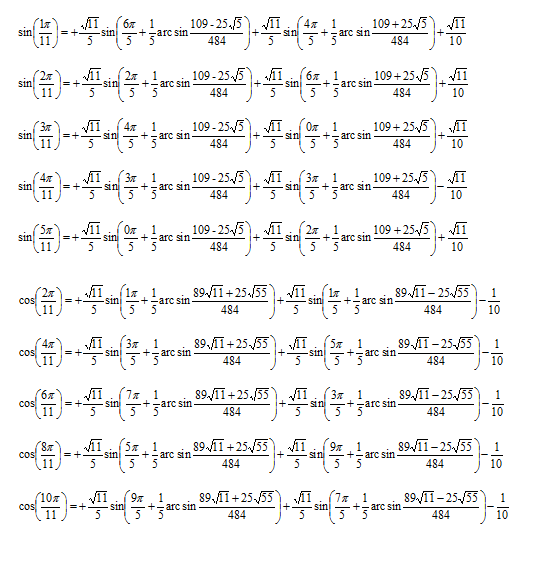

 i).
i).



 0 esetén nem integrálható.
0 esetén nem integrálható.