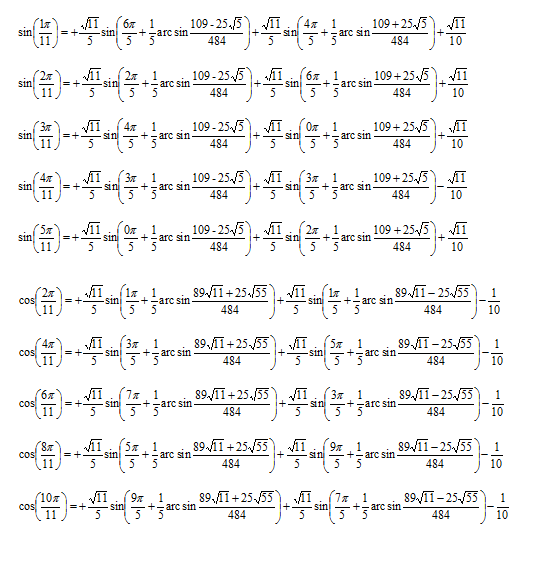| [694] marcius8 | 2013-04-23 14:51:57 |
 Egy újabb problémával szembesültem. Középiskolában tanítok matematikát, és például geometriai feladatok akkor könnyen megoldhatóak illetve a geometriai feladatok megoldásai akkor javíthatóak könnyen, ha a feladatok adatai és eredményei egész számok. Például szerencsés olyan derékszögű háromszöggel számolni, amelynek oldalai egész számok --> pitagoraszi számhármasok. A feladat a következő: Keressünk olyan derékszögű tetraédert, amelynek minden éle egész szám. (Egy tetraéder akkor derékszögű, ha van olyan csúcsa, amelyből kiinduló három él páronként egymásra merőleges.) Számítógéppel ilyent könnyű találni: Az "OABC" tetraéder "O" csúcsából kiinduló élek páronként merőlegesek egymásra, és OA=44, OB=117, OC=240, ekkor AB=125, BC=267, CA=244. Lehet ezeket a tetraédereket úgy generálni, mint a pitagoraszi számhármasokat?
|
|
| [693] marcius8 | 2013-04-22 15:40:09 |
 Köszönöm szépen mindenkinek a segítséget, most már a megadott oldalak rendesen jelennek meg. A segítségért küldök a nekem segítőknek virtuálisan egy jó nagy tábla csokit. Tisztelettel: Bertalan Zoltán
|
 |
| Előzmény: [692] Erben Péter, 2013-04-22 10:42:05 |
|
| [692] Erben Péter | 2013-04-22 10:42:05 |
 Az oldal MathML kóddal írja le a képleteket. Ennek megjelenítése - tudomásom szerint - csak Firefox alatt működik plugin nélkül. A többi böngészőt fel kell okosítani hozzá.
|
| Előzmény: [691] marcius8, 2013-04-22 10:29:13 |
|
| [691] marcius8 | 2013-04-22 10:29:13 |
 Köszönöm szépen az ajánlott oldalakat. Sajnos nem igazán tudtam értelmezni az oldalak tartalmát, pedig pont erre vagyok kiváncsi. Az oldalakon a képletekből eltűntek a műveleti jelek nagy része (gyökvonás, osztás, stb...) és a képletekben szereplő számokról nem lehet eldönteni hogy indexek, hatványkitevők vagy mások.
Például: "For i=1,...,10 let t i be equal to t where every béta has been replaced by béta i. Then alfa=t 1 +...+t 10 10 =t 1 10 10 +...++t 10 10 10 10"
A "Gauss módszere" oldal tartalma emiatt számomra teljesen értelmezhetetlen. Arra kérlek, hogy ha tudsz ezeknek az oldalaknak a javított tartalmáról, irjál róla. Előre is köszönöm: Bertalan Zoltán.
|
| Előzmény: [690] Lóczi Lajos, 2013-04-18 23:14:52 |
|
| [690] Lóczi Lajos | 2013-04-18 23:14:52 |
 Ekkor "sin(pi/11)" algebrai alakjának nevezem azt a kifejezést, amely az "f" polinom együtthatóiból állítható elő a négy alapművelet (összeadás, kivonás, szorzás, osztás) valamint gyökvonás segítségével.
A műveletek véges sokszori alkalmazására gondolsz?
Csak 11-nél kisebb kitevőjű gyököket szeretnél látni?
Ha igen és igen, akkor elég az egységgyökökre szorítkozni (onnan a szinusz konjugálással kifejezhető).
Az alábbi oldalakat ajánlom:
Gauss és a 17-szög, Vandermonde módszere, Gauss módszere általában.
|
| Előzmény: [689] marcius8, 2013-04-18 08:05:02 |
|
| [689] marcius8 | 2013-04-18 08:05:02 |
 Amit a [675]-ben írtam, az nem a "sin(pi/11)" algebrai alakja. tekintsük azt az egész együtthatós "f" polinomot, amelynek gyöke a "sin(pi/11)". Ekkor "sin(pi/11)" algebrai alakjának nevezem azt a kifejezést, amely az "f" polinom együtthatóiból állítható elő a négy alapművelet (összeadás, kivonás, szorzás, osztás) valamint gyökvonás segítségével. Ezt előállítja valahogyan a Mathematica nevű program is, de ezt oldalakon keresztül teszi (kedvem nincs ennek a kifejezésnek a tanulmányozásához). Ráadásul ez a program azzal fenyegetődzik, hogy "sin(pi/23)" algebrai alakja reménytelenül hosszú. Akkor másképp teszem fel a kérdést: Tekintsük azt az egész együtthatós "f" polinomot, amelynek gyöke a "sin(pi/prím)" kifejezés. Hogyan lehet ennek az "f" polinomnak a gyökeit előállítani az "f" polinom együtthatóiból állítható elő a négy alapművelet (összeadás, kivonás, szorzás, osztás) valamint gyökvonás segítségével?
Egyszerűbb esetekben (prím=3, 5, 7, 13, 17, 19, és általában az olyan prímek esetén, ahol a prímből 1-et elvéve egy olyan szorzat adódik, amely csak 2-vel és 3-mal osztható) elő tudom állítani "sin(pi/prím)" albegrai alakját, igaz, ezekben az esetekben mindig másodfokú és harmadfokú egyenleteket kell megoldani.
|
| Előzmény: [688] Lóczi Lajos, 2013-04-17 15:19:03 |
|
|
| [687] marcius8 | 2013-04-17 12:38:52 |
 Köszönöm szépen a megoldást, ezért virtuálisan tudok küldeni egy boci-csokit. A következő (igazi) kérdésem az, hogy ha nem írtam volna le a sejtést, akkor hogy lehet kitalálni a "sin(pi/11)" algebrai alakját, feltéve ha tudjuk, hogy a sin(pi/11) gyöke a 1024x10-2816x8+2816x6-1232x4+220x2-11=0 egyenletnek.
Általában hogy lehet megtalálni a "sin(pi/prím)" algebrai alakját, feltéve ha ismerünk egy olyan egész együtthatós polinomot, amelynek gyöke a "sin(pi/prím)"? Például prím=11, 23, 29, 31, stb....
Tisztelettel: Bertalan Zoltán
|
 |
| Előzmény: [684] Lóczi Lajos, 2013-04-15 23:39:59 |
|
|
|
| [684] Lóczi Lajos | 2013-04-15 23:39:59 |
 Ha a jobb oldalon szereplő egyik szinuszt elnevezed M-nek, a másikat P-nek, majd ezekre a definiáló egyenletekre külön-külön ráhatsz arkusz szinusszal, lineáris rendezéssel és szinusszal, és egyszerűsítünk, akkor azt kapjuk, hogy
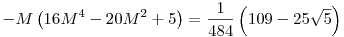 és és 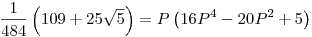 . .
Ebből adódik, hogy P-M gyöke a 3872x5-9680x3+6820x2-880x-109=0 egyenletnek, és így 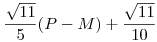 gyöke az 1024x10-2816x8+2816x6-1232x4+220x2-11=0 egyenletnek. gyöke az 1024x10-2816x8+2816x6-1232x4+220x2-11=0 egyenletnek.
|
| Előzmény: [683] marcius8, 2013-04-15 15:55:49 |
|
| [683] marcius8 | 2013-04-15 15:55:49 |
 Először is köszönöm, hogy többen foglalkoztak az általam felvetett [675] összefüggésekkel.
Néhány reagálás a részemről:
[681] hozzászólás: Az rendben van, hogy az általam említett összefüggés bal oldala a hozzászólásban említett egyenlet legkisebb pozitív gyöke (addíciós tételek segítségével ez belátható), de hogy mutatjuk meg, hogy általam említett összefüggés jobb oldala is a hozzászólásban említett egyenlet legkisebb pozitív gyöke?
[680] hozzászólás: Csakugyan, euklideszi szerkesztési lépésekkel (csak egyélű és beosztás nélküli vonalzó és körző használható, két ponton átmenő egyenes húzható, két egyenes metszéspontja jelölhető, adott középpontú és adott sugarú kör szerkeszthető, egyenes és kör metszéspontja jelölhető, két kör metszéspontja jelölhető), csak a hozzászólásban említett szabályos sokszögek szerkeszthetők. De mi van akkor, ha megengedjük az egyélű vonalzó illesztését is? Erre példa a "www.gszi.sulinet.hu"-->"tanulói információk" fül-->"Bertalan Zoltán" helyen lehet példákat látni. (szögharmadolás, déloszi probléma, szabályos 7-szög szerkesztése)
Még egy kérdés: Feltéve, ha tudjuk, hogy az első összefüggésem helyes, ezt az összefüggést felahsználva hogy lehet bizonyítani a többi összefüggést?
Köszönöm mégegyszer az eddigi hozzászólásokat, mindenkinek kívánok jó gondolkozást: Bertalan Zoltán.
|
|
|
| [681] Lóczi Lajos | 2013-04-12 22:29:03 |
 Csak az első formuládat ellenőriztem. Ez pl. azért igaz, mert a bal oldal is és a jobb oldal is mindketten az
1024x10-2816x8+2816x6-1232x4+220x2-11=0 egyenlet legkisebb pozitív gyökével egyezik meg.
|
| Előzmény: [675] marcius8, 2013-04-12 12:52:40 |
|
| [680] Maga Péter | 2013-04-12 18:06:20 |
 Először röviden vázolom, hogy bizonyítja be az ember, hogy a szabályos 11-szög nem szerkeszthető. Miből áll a szerkesztés egy lépése? Általában véve sokféle lehet, de pontot csak háromféleképp kaphatsz: veheted már meglévő két egyenes, két kör vagy egy egyenes és egy kör metszéspontját (már meglévő egyenes: két pontja ismert, már meglévő kör: középpontja és egy kerületi pontja ismert). Most pakoljunk be mindent koordináta rendszerbe, kezdetben adottak mondjuk a (0,0) és (1,0) pontok. Ezek után mindig, amikor új pontot kapunk, annak mindkét koordinátája kifejezhető racionális számokból az alapműveletek és négyzetgyökvonás segítségével. Ezt indukcióval könnyű bebizonyítani: ilyen pontokra illeszkedő egyenesek metszéspontja ilyen stb.
Valójában áttérhetünk pontok szerkesztéséről számok szerkesztésére. Egy szabályos 11-szög szerkesztése ekvivalens a cos (2k /11) (vagy sin (2k/ /11) (vagy sin (2k/ /11) számok) szerkesztésével k=1,...,10-re. Ezek a számok viszont nem kaphatók meg a racionális számokból pusztán alapműveletekkel és négyzetgyökvonással. /11) számok) szerkesztésével k=1,...,10-re. Ezek a számok viszont nem kaphatók meg a racionális számokból pusztán alapműveletekkel és négyzetgyökvonással.
Van az algebrában egy olyan fogalom, hogy test. Ez egy olyan halmaz, amin összeadást, kivonást, szorzást, osztást tudsz végezni a szokásos műveleti tulajdonságokkal (tagok felcserélhetősége, csoportosíthatósága, zárójelfelbontás). A racionális számok például testet alkotnak. Hasonló módon testet alkotnak az 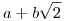 alakú (a,b racionálisok) számok is, ez a test tartalmazza Q-t. Ehhez hasonló esetekben lehet arról beszélni, hogy egy test egy másik felett hányadfokú. Ez lényegében az, hogy veszel egy olyan alakú (a,b racionálisok) számok is, ez a test tartalmazza Q-t. Ehhez hasonló esetekben lehet arról beszélni, hogy egy test egy másik felett hányadfokú. Ez lényegében az, hogy veszel egy olyan  elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a 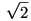 ilyen: ha hozzáveszed Q-hoz, utána már minden más előáll az alapműveletekkel), és kiszámolod, legalább hányadfokú F1-beli együtthatós polinomnak a gyöke ilyen: ha hozzáveszed Q-hoz, utána már minden más előáll az alapműveletekkel), és kiszámolod, legalább hányadfokú F1-beli együtthatós polinomnak a gyöke  . A konkrét példában: . A konkrét példában: 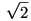 nem gyöke egyetlen Q együtthatós elsőfokú polinomnak sem (hiszen irracionális), de másodfokúnak már igen: x2-2 (az ilyen legkisebb fokú polinomot hívjuk minimálpolinomnak). Tehát a konkrét példában ez a fok 2. A szerkesztendő számok nyelvén mindig ilyen történik: ha az eddig megszerkesztett számok benne vannak egy F1 testben, akkor a következő megszerkesztett szám benne lesz egy olyan F2 testben, ami vagy maga F1 (nincs bővítés), vagy pedig F1 egy másodfokú bővítése. Bővítés bővítése esetén a fokszámok összeszorzódnak. Így ha sokszor bővítünk, akkor is mindig olyan számaink lesznek csak, amiknek a Q feletti minimálpolinomjának foka 2-hatvány. Viszont cos (2 nem gyöke egyetlen Q együtthatós elsőfokú polinomnak sem (hiszen irracionális), de másodfokúnak már igen: x2-2 (az ilyen legkisebb fokú polinomot hívjuk minimálpolinomnak). Tehát a konkrét példában ez a fok 2. A szerkesztendő számok nyelvén mindig ilyen történik: ha az eddig megszerkesztett számok benne vannak egy F1 testben, akkor a következő megszerkesztett szám benne lesz egy olyan F2 testben, ami vagy maga F1 (nincs bővítés), vagy pedig F1 egy másodfokú bővítése. Bővítés bővítése esetén a fokszámok összeszorzódnak. Így ha sokszor bővítünk, akkor is mindig olyan számaink lesznek csak, amiknek a Q feletti minimálpolinomjának foka 2-hatvány. Viszont cos (2 /11)+isin (2 /11)+isin (2 /11) minimálpolinomja x10+x9+...+x+1, ami tizedfokú. /11) minimálpolinomja x10+x9+...+x+1, ami tizedfokú.
Általában is ez a procedúra. A szabályos n-szög szerkeszthetősége visszamegy az n. körosztási polinomra: ez az xn-1 egyik tényezője, a cos (2 /n)+isin (2 /n)+isin (2 /n) minimálpolinomja. Ennek foka pedig /n) minimálpolinomja. Ennek foka pedig  (n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk. (n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk.
Ezek mély dolgok. Majd tanulod:).
(Ez csak egy sebtében írt vázlat, de ha valamit elírtam, majd valaki kijavít.)
|
| Előzmény: [678] w, 2013-04-12 17:03:12 |
|
|
|
|
|
| [675] marcius8 | 2013-04-12 12:52:40 |
 Nagyon hálás lennék annak, aki a következő összefüggések bármelyikét bizonyítani tudja. Ezeket az összefüggéseket én csak megsejtettem, ugyanis mindenképpen egy szabályos 11 oldalú (!) sokszöget akartam szerkeszteni.
|
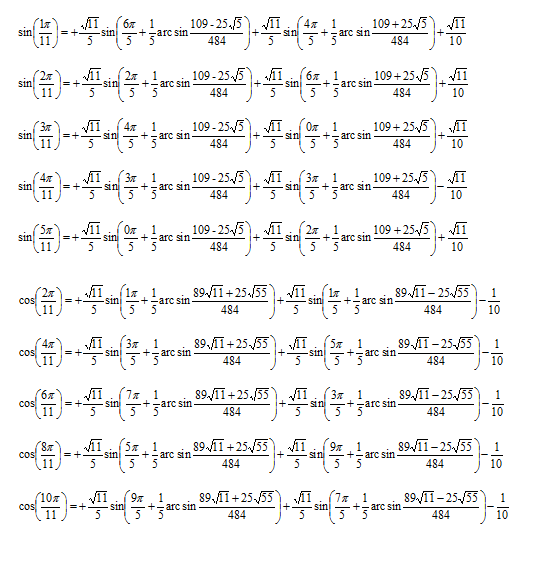 |
|
| [674] w | 2013-04-08 16:38:02 |
 Na szóval,
1. Mennyi a négyzetszámok lehetséges maradéka 3-mal osztva (kérlek, használd fel, amit írtam korábban, és írd le a megoldást ide)?
2. Miért nincs négyzetszám a következő számok között: 11, 101, 1001, ... ? (Segítség: vajon mennyi lesz a 3-as maradékuk?).
|
| Előzmény: [673] nyerek01, 2013-04-08 02:04:18 |
|
|
| [672] w | 2013-04-06 20:31:46 |
 Kis lökés rajta: először keressük meg a legfeljebb n-edfokúakat. Igazoljuk, hogy pontosan egy van. Konstruáljuk is meg azt. Az általános eset ennél nehezebb, azt még nem oldottam meg.
(Ez ismert feladat. A hozzáértők kérem, ne lőjék le.)
|
| Előzmény: [669] w, 2013-04-01 20:26:25 |
|
| [671] w | 2013-04-06 20:11:54 |
 Ez nem nehéz feladat. Osszuk el az n számot maradékosan 3-mal: n=3k+r (n, k egész szám; r lehet 0, 1 vagy 2). Ekkor mennyi lesz n2? Ebből megállapítható n2 3-as maradéka. Meglepő eredmény.
Próbáld megoldani akkor a következő feladatot. Hány négyzetszám van a következő számok között: 1, 11, 101, 1001, 10001, ...?
|
| Előzmény: [670] nyerek01, 2013-04-06 17:09:12 |
|
| [670] nyerek01 | 2013-04-06 17:09:12 |
 Bizonyítsa hogy: nincs négyzetszám, ami hárommal osztva kettőt ad maradékul (bocs ha rossz helyre írtam, mert kevés az itteni szinthez)
|
|






 /11) algebrai alakja?
/11) algebrai alakja?


 elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a
elemet, amit a kisebb F1-hez hozzá kell venni, hogy a nagyobb F2-t kapd (a konkrét példában a  (n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk.
(n), az n-hez relatív prím maradékosztályok száma, és ez pontosan azokban az esetekben 2-hatvány, amit Csimby írt. És ez itt szerkeszthetőséget is jelent: a fent leírt dolgoknak a konkrét esetben van egy 'akkor és csak akkor' természete, de ezzel óvatosan! Általában nem igaz, hogy aminek a minimálpolinomja 2-hatvány fokú, az szerkeszthető; az xn-1 gyökeinek van még egy tulajdonsága, amit itt suba alatt használunk. 

 0 és pi-k páronként különböző Fermat-prímek, tehát olyan alakú prímek, mint amit te is írtál: 22r+1.
0 és pi-k páronként különböző Fermat-prímek, tehát olyan alakú prímek, mint amit te is írtál: 22r+1.