Fórum: Híres(?) álbizonyítások

Szeretnél hozzászólni? Jelentkezz be.

[32] joe	2004-08-07 18:16:11
A sárga bableveshez: ez egy Gödel-féle csapda, ha feltesszük, hogy utálom a sárga bablevest, akkor a második állítás olyan, mint a következő "Ez az állítás hamis." Ez pedig értelmetlen, függetlenül az ízlésemtől. Innentől a megoldás triviális. (Bocs, direkt volt...)
Előzmény: [18] Gubbubu, 2004-01-20 19:04:44

[31] nadorp

2004-07-29 10:34:33

Egy kicsit javítanék.Az általam írt második egyenlőség értelmetlen, a végét el kell hagyni, helyesen

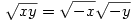
$\sqrt{xy}=\sqrt{-x}\sqrt{-y}$

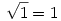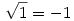Lényegében azt akartam vázolni, hogy $\sqrt1=1$ és $\sqrt1=-1$ fennállásából még nem következik, hogy 1=-1. Az egynlőségláncot a gyökvonás többértékűsége mitt nem szabad ebben a formájában felírni.

Előzmény: [30] nadorp, 2004-07-29 10:21:04

[30] nadorp

2004-07-29 10:21:04

A félreértést az okozhatja, hogy a gyökvonást milyen számkörön alkalmazzuk. Ha valós számkörön, akkor a leírt egyenlőséglánc szóba se jöhet. Ha a komplex számkörön, akkor, mivel a gyökvonás többértékű művelet, ezért a leírt egyenlőséglánc nem ellentmondásos, hanem csak egyszerűen "rosszul" vontunk gyököt. "Sajnálatos módon" a komplex számok körében a

$\sqrt{xy}=\sqrt{x}\sqrt{y}$ egyenlőség és a

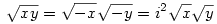$\sqrt{xy}=\sqrt{-x}\sqrt{-y}=i^2\sqrt{x}\sqrt{y}$ egyenlőség egymástól függetlenül igaz, de ebből még nem következik, hogy 1=-1.

Előzmény: [29] miklosi, 2004-07-28 13:20:31

[29] miklosi	2004-07-28 13:20:31
$1 = \sqrt{1} =\sqrt{(-1)(-1)} = \sqrt{-1} \sqrt{-1} = i^2 = -1$

[28] ScarMan

2004-03-02 18:22:46

Szia Csimby!

Amit leírtál, az mind igaz, csak az utolsó mondat nem illik oda. Az addig ok, hogy 9*3+2=29, csakhogy ennek az összegnek semmi oka nincs arra, hogy 30 dollár értékű legyen! A 30 dollár az az összeg, amennyi pénzük a vendégeknek volt, a 29 dollár pedig abból tevődik össze amennyit a vendégek ebből a pénzből kifizettek, valamint amit a pincér ellopott tőlük. Csakhogy az a 2 dollár, amit a pincér ellopott tőlük, megjelenik a 9*3 szorzatban is, hiszen azt ők kifizették (így került a pincérhez)! Semmi okunk arra, hogy a két szám összegét vegyük, mert ezzel nem kapjuk meg azt, hogy a vendégeknek eredetileg mennyijük volt. A két szám összege azt adja meg, hogy a vendégek mennyit költöttek, a pincér által ellopott pénzt kétszer számolva.

Remélem jól csináltam;) ScarMan

Előzmény: [25] Csimby, 2004-02-23 00:46:16

[27] Csimby	2004-02-23 23:02:10
Oké, te bebizonyítottad, hogy nem tűnt el, én bebizonyítottam, hogy eltűnt, de honnan tudod, hogy neked van igazad? Azaz hol van a hiba az enyémben? (feltéve, hogy tényleg nem tűnt el a dollár :)

[26] ágica	2004-02-23 21:09:05
Az első esetben tekinthetjük úgy, hogy a három barát mindegyikének -10 dollárja van, a pincérnek pedig +5, ez összesen -25 dollár, azaz a szoba ára. Miután a pincér odaadja nekik a pénzt, mindhármuknak -9 dollárjuk lesz, azaz összesen -27, a pincérnek viszont +2, amit ehhez hozzáadva szintén a szoba árát, -25 dollárt kapunk, tehát nem tűnt el egy dollár sem :)
Előzmény: [25] Csimby, 2004-02-23 00:46:16

[25] Csimby

2004-02-23 00:46:16

Harom barat megall egy motelben. Mivel csak egy szoba volt szabadon, ezert kozosen kivettek azt. A szoba ara egy ejszakara 30 dollar, ezt elosztottak harom fele, igy fejenkent fizettek 10 dollart, majd felmentek. Hamarosan eszrevette a recepcios, hogy nem jo arat mondott, a szoba csak 25 dollarba kerul, a szobapincerrel utanuk kuldte a kulonbozetet, 5 dollart. A pincer - mivel nem tudta elosztani harom fele, mindharmuknak adott 1 dollart, a maradek 2 dollart meg zsebretette.

Ez igy ugye azt jelenti, hogy mindharman 9 dollart fizettek a szobaert, 9*3=27, a pincernel maradt 2 dollar, ez osszesen 29 dollar.

De hova tunt 1 dollar?

[24] Csimby

2004-01-27 19:52:54

Jó, akkor tennék azért egy kis kiegészítést mert úgyérzem félreérthető voltam, és nem akarok rossz pontot szerezni :-) -> Nálunk csak mi (diákok) mondjuk, hogy innentől triviális, ha nem értjük, és nem a tanárok.

Valaki mesélt erre egy sztorit: "Egyetemen prof.: Innentől triviális! - ezek után 1/2 órát gondolkozik a teleírt tábla előtt majd megszólal: Rendeben van tényleg triviális."

[23] Gubbubu

2004-01-26 20:08:39

Kedves Csimby!

Pontosan erről beszélek! A "triviális" egy teljesen szubjektív fogalom, ami valakinek triviális, az másnak nem feltétlenül az! Ezért lehetséges visszaélni vele, és triviálisnak mondani olyan dolgokat, amit a tanár egész egyszerűen lusta bebizonyítani, vagy amit egyenesen nem tud! És ez nekem a halálom! Amikor valakinak két napja van egy vizsgára felkészülni az egyetemen, és a tankönyv/jegyzet minden második szava az, hogy "ez triviális, nem akarjuk a Kedves Olvasót a gondolkodás örömétől megfosztani...", akkor a Kedves Olvasó szívrohamot, agyérgörcsöt és idegsokkot szokott kapni a gondolkodás öröme helyett! Hát hol ebben az öröm, könyörgöm? És ez mind egyetlen szócska miatt: Triviális!

Egy szó mind fölött, egy szó kegyetlen,

Egy a sötétbe zár, bilincs az egyetlen...

Üdv:G.

Előzmény: [22] Csimby, 2004-01-26 19:43:46

[22] Csimby	2004-01-26 19:43:46
Mi akkor mondjuk matekórán valamire, hogy: "innentől már triviális", ha nem látjuk hogyan kéne folytatni... :-)

[21] Gubbubu

2004-01-26 19:04:35

Kedves László!

Örülök, hogy tetszett. Gondolkodtam egy kicsit, elmondjam-e most, mi motivált igazából a "bizonyítás" közreadásában, nem akar-e még más is gondolkodni rajta, de mivel ez a topik hosszú idők óta nem tűnik túl-túl népszerűnek (ehhez -hehehe - hozzájárulhat az is, hogy én írom ide a hozzászólások legtöbbjét..:-), inkább végleg "lelövöm a poént".

Tehát: a bizonyítás minden részlete egy kivételével igaz, az n=0 "kezdőeset" teljesül, a hiba a k->k+1-re vonatkozó bizonyítás egyik kicsi részletében van (a többi "részlet" alapjában véve nem csalás). Nevezetesen: a 3^k szám nem feltétlenül (teljes, valódi) 3-hatvány. A k=0-ra 3⁰=1, és ennek persze 3 nem osztója, sem "triviálisan", sem egyébként (épp az ilyen "triviálisan igaz" állítások szoktak végül mindig hamisnak bizonyulni...). Ezért k=0-ra működik a dolog, de az "áttérés" k=0-ról k=1-re már nem. És innentől kezdve persze rossz az egész.

A dolog 1. tanulsága tehát az, amit említettél. A 2. tanulság az, hogy ha formulákkal bánunk, nagyon alaposan vigyáznunk kell az értelmezési tartományukra. A 3^k formulát kicsit másképp értelmezzük a k=0 esetben, mint egyébként. A 3. tanulság, hogy a "triviális" szónak nincs igazán helye és értelme a matematikaoktatásban. Illetve: ennek a szónak is megvan a sajátos értelmezési tartománya, nem szabadna visszaélni vele, mást jelent egy kis közösségben, mint egy nagyobban.

Üdv: M.Á.

Előzmény: [20] lorantfy, 2004-01-25 21:24:57

[20] lorantfy

2004-01-25 21:24:57

Kedves Gubbubu!

Nagyon szellemes ez az indukciós álbizonyításod és persze nagyon tanúságos is.

A teljes indukció lényege, hogy a kifejezésre jellemző tulajdonság „öröklődését” bizonyítjuk.

Nemhiába mondja a tanár a matekórán, hogy nézzük meg igaz-e a bizonyítandó tulajdonság az első pár „n” értékre, nehogy valami olyan állítást vigyünk tovább, ami speciálisan csak az 1. elemre igaz.

Hát itt pont ez a helyzet. Ez a tulajdonság – mármint, hogy az összeg páratlan – csak n=0-ra igaz.

Előzmény: [19] Gubbubu, 2004-01-24 12:56:34

[19] Gubbubu

2004-01-24 12:56:34

Kedves Fórumosok!

Az "Ujjgyakorlatok" topikban Suhanc egyik feladata ihlette a következő "bizonyítást":

Indukcióval belátjuk minden n $\in$ N-re, hogy 3|2ⁿ+3ⁿ+5ⁿ.

n=0-ra 3|2⁰+3⁰+5⁰=1+1+1=3; Ha pedig igaz valamely k-ra az állítás, akkor k+1-re is, mivel 2^k+1+3^k+1+5^k+1=2^.2^k+3^.3^k+5^.5^k=

=2^.(2^k+3^k+5^k)+3^k+3^.5^k; és ennek a kifejezésnek a 3 osztója, mivel 2^.(2^k+3^k+5^k) második tényezőjének az indukciós feltevés miatt osztója, a 3^k 3-hatványnak triviálisan, a 3^.(5^k) tagnak pedig az első tányezőjét osztja, tehát egy összeg minden tagját, s így az összeget is osztja 3.

Ezzel állításunkat bizonyítottuk. Tehát pl. 3|2²+3²+5²=4+9+25=38=33+3+2.

[18] Gubbubu

2004-01-20 19:04:44

Egy látszólag teljesen ártalmatlan cédulán a következő két állítás olvasható: .

1. Szereted a sárga bablevest;

2. Ezen a lapon pontosan két állítás hamis.

Bebizonyítom bárkinek, hogy él-hal a sárga bablevesért. Megmutatom neki a fenti cédulát.

Az első állításnak igaznak kell lennie. Ha ugyanis hamis, akkor ha a második mondat igaz, akkor kell még egy hamis állításnak lennie a cédulán, tehát a második állítás is hamis. A második mondat tehát nem igaz (már feltéve, hogy az első hamis), hiszen ha igaz, akkor hamis. Vagyis ha az első állítás hamis, a második mondat is hamis. Ez esetben azonban két hamis állítás van a lapon, vagyis a második állítás igaz. Tehát (feltéve, hogy az első mondat hamis) a második állítás hamis sem lehet, hiszen ekkor igaz.

Azaz ha az első állítás hamis, a második se nem igaz, se nem hamis. Ez ellentmondás, így az első állítás igaz. A szerencsétlen áldozat szereti a sárga bablevest.

Ennek a bizonyítási módszernek a gyakorlati jelentősége óriási. A vonakodó gyerek rávehető, hogy megegye a sárgarépafőzeléket, a vonakodó szülő, hogy zsebpénzt emeljen, bármely elegendően csinos nőnek azonnal bizonyítható, hogy világéletében a cédulatulajdonossal akart vacsorázni stb., és így tovább. Vagy talán van valami hiba a gondolatmenetben?

[17] Gubbubu	2004-01-14 00:45:12
Kedves László! Végre, végre! Már kezdtem azt hinni, hogy meg nem értett zseni vagyok (megértett zseni lettem)! Köszönöm az ábrákat! Most már csak rendszertesztelés végett kell föltennem az általam készített ábra (remélem) jobban látható, nagyobb változatát, mivel ez délután nem sikerült (elfelejtettem JPG-be konvertálni): És hogy ne haljon ki ez a téma, íme egy feladat (forrás Courant-Robbins: Mi a matematika? c. könyve). Holnapra este hozok még egyet, ha megtalálom. 6. feladat: Belátjuk, hogy tetszőleges két pozitív egész szám egyenlő. Tekintsük az alábbi A(n) állítást: "Ha a,b olyan pozitív egész számok, hogy max(a,b)=n, akkor a=b." (max(a,b) az az {a,b} halmazbeli m szám, amelyre a,b $\leq$ m) n=1-re ha max(a,b)=1, azaz 0<a,b $\leq$ 1, akkor nyilván a=b=1. Ha n=k-1-re (k>1) igazoltuk a sejtést, akkor amennyiben max(a,b)=k, egyszerűen igazolható max(a-1,b-1)=k-1. Pl. ha max(a,b)=a(=k), akkor b $\leq$ a, ekkor b-1 $\leq$ a-1, azaz max(a,b)=a-1(=k-1). Egyszóval max(a,b)=k-1, és ekkor az ind. felt. miatt a-1=b-1, azaz a=b. Q.E.D. Hol hibáztunk?

Előzmény: [16] lorantfy, 2004-01-14 00:17:05

[16] lorantfy	2004-01-14 00:17:05
Kedves Gubbubu! Köszönet a részletes magyarázatért! Értem miről van szó. A lényeg, hogy nem csak osztópontban lehet elvágni.

Előzmény: [14] Gubbubu, 2004-01-13 20:33:55

[15] Gubbubu

2004-01-13 21:00:50

Egy megoldásféle a 2. feladatra: Egyszerűen nem igaz az n=1 eset. Az egyelemű halmazban lévő szerencsétlen ló azonos színű - önmagával, de nem feltétlenül azonos színű a többi lóval. Azt kellene bizonyítani, hogy ez a ló azonos színű a többi lóval, mivel ezt látjuk be az n>1 esetekben is. Márpedig ez a ló nem feltétlenül azonos színű a többi lóval, hisz sokféle színű lovak léteznek. Egyébként ettől függetlenül, és hasonló logikai okfejtés alapján, az n->n+1 átmenet sem működik, így az okoskodás kétszeresen is rossz (próbáljuk meg az "áttérést" n=1-ről 2-re!) Az "azonos színű" kifejezést itt többféle értelemben használtuk, tulajdonképp az n=1 esetben és az n>1 esetben ezek teljesen más állítások. Így valójában ez nem egy teljes teljes indukciós bizonyítás.

[14] Gubbubu	2004-01-13 20:33:55
Kedves László! Értem, mire gondolsz, de látom, ez fordítva nem igaz. Ábrán egyszerű (remélem, látszik, az ábrarajzolás és méretezés még nem igazán megy nekem): Valóban, (mondjuk egyenesekkel összekötött vagy ilyennek képzelt), de mindenesetre egyenesek mentén elhelyezkedő pontokat/pöttyöket nevezzünk "háromszögoldalaknak"! Igaz, hogy az euklideszi, folytonos síkmodellben ha egy egyenest vagy szakaszt két részre osztunk, mindig van "osztópont", ám miért ragaszkodnánk mindig ehhez az elavult szemlélethez? Szerintem jogom van azt mondani, hogy a lenti ábrán egy 6 pötty oldalú háromszög minden oldalát három egyenlő részre (2 pöttyöt tartalmazó "szakaszokra") osztottuk, még akkor is, ha nincs olyan pont, ami osztópont lenne, és mindkét "szakaszhoz" tartozna. Na mindegy, ha nincs, hát nincs (mármint jogom ezt mondani). A feladat megfogalmazása kicsit pontatlan volt, de ez csak részben az én hibám, hiszen egyszerűen nem szoktuk meg, hogy a síkgeometria "diszkrét" modelljeiről beszéljünk, hiányoznak a fogalmaink és jelöléseink, így egy részletesebb magyarázat még ennél is hosszabb hozzászólást igényelt volna. De azt hittem, szemléletesen érthető lesz, hiszen azt az utasítást is meg szoktuk érteni, hogy "rakjuk ki a 10 számot háromszög alakban", néhány példaábra felrajzolása után.

Előzmény: [12] lorantfy, 2004-01-12 09:17:14

[13] Hajba Károly

2004-01-13 10:42:37

Mivel lassan egy hónapja fel lett adva ez a miniátverés, s nem reagált rá senki, így "lelövöm".

A kezdeti feltételben szerepelt a a=b feltétel, így (a-b)=0, így ezzel nem lehet osztani. :o)

Előzmény: [8] lorantfy, 2003-12-23 12:35:33

[12] lorantfy	2004-01-12 09:17:14
Kedves Gubbubu! Ha azt mondod, hogy legyenek az élek a pontok az ábrán akkor értem, különben nem! Ekkor, csak egyel csúszik a számozás.

Előzmény: [11] Gubbubu, 2004-01-10 01:25:10

[11] Gubbubu

2004-01-10 01:25:10

Üdv, Kedves László (ugye?), Üdv Fórum!

Először is köszönöm a megoldást, és külön az ábrákat!

Másodszor, az első, gondolatmenetemben talált hiba valójában nem áll fennt. Azaz fennáll, de csak azért, mert MÁR MEGINT PONTATLANUL FOGALMAZTAM MEG EGY FELADATOT! (elnézést, magammal ordibálok, nem veled. Ugye hallod a falak kongását? Az én fejem oda-odaütődése okozza. Azt hiszem, ideje lenne megváltoztatnom a "Gubbubu" nevet mondjuk "Untermensch"-re).

Valójában a 36 oldalú nagy háromszög oldalait nem mint folytonos szakaszokból összetevődő háromszöget kell elképzelni (bár ez segít a feladat megoldásában és a szituáció elképzelésében, de csak pontatlan képe a valóságnak).

Én egyfajta hiperdiszkretizált-kvantumiko-atomisztikus felosztásra gondoltam, ti. hogy minden "szakasz" azonos számú pontot tartalmazzon. Az a baj, hogy nem tudok ábrát rajzolni, de talán érthető, mire gondolok. A "szakaszok" "egyenlő felosztásának" kritériuma nem a hossz, hanem az, hogy egyenlő számú pöttyöt tartalmazzanak! A 36 pötty oldalú háromszög minden oldala mentén így 36 = 3-szor 12 pötty van, és egy "szakasz" 12 pöttyből áll.

Harmadszor, a megoldásod azonban enek ellenére - ha a konkrét számoktól eltekintünk - tökéletes. A konkrét számok nem fontosak, mert álbizonyításunk szinte bármelyik összetett háromszögszámra átfogalmazható (és a prím háromszögszámok elég ritkák), csak azért választottam n=36-ot, hogy a 666-os "sátánista" körítés megfelelően ördögi legyen, illetve hogy ne lehessen pontos ábrát rajzolni - abból persze rögtön kiderülne, amit így is kiderítettél, hogy...

... hogy valóban hamis lemma volt az álbizonyításban, mégpedig az általad mondott, ti. hogy minden "kis" háromszögben 78 pötty van. A 36 oldalú szabályos háromszöget tényleg nem lehet "diszkrét" módon (ld. előző előtti bekezdés) úgy darabolni,hogy minden kis háromszög egyforma legyen, vagy ha lehet is, akkor néhány kisebb háromszög "határa" egybeesik, azaz néhány pöttyöt többször számolunk. Valószínűségszámítási feladatok megoldásánál típushiba bizonyos kimenetelek többször számolása, és most sem szerencsés (ez lenne eme szerény kis feladat egyik didaktikai tanulsága, a másik, hogy a tér folytonos és diszkrét modelljének egyidejű használatakor legyünk óvatosak! Ne keverjük!).

Mészáros Árpád

Előzmény: [10] lorantfy, 2004-01-09 13:52:18

[10] lorantfy	2004-01-09 13:52:18
Kedves Gubbubu! Ördögi ez a feladat, de azért feloldható az ellentmondás. Két probléma is van. Az egyik, hogy a 36. tagnál a háromszög oldalán csak 35 egyenlő szakasz van, így nem osztható 3 egyenlő részre. Ez a felosztás a 37. tagnál lehetséges és itt S(37)=703. A keletkező kis háromszögek oldalán 12 szakasz van, tehát 13 pont, így ezek a sorozat 13. tagját jelképezik. S(13)=91. A második probléma, hogy ezt a számot nem szorozhatjuk 9-el, hiszen vannak közös csúcsok és közös élek és ezeket a pontokat többször számolnánk. A 91 pontból 36 van a kerületen, így a belső pontok száma: 55. Ha a csúcspontokat levonjuk, akkor minden élen 11 pont van. A kisháromszögek pontjait úgy számoljuk össze, hogy 9-szer vesszük a belső pontokat: 955=495, majd az éleken lévő pontokat: 1811=198, majd hozzáadjuk a 10 csúcspontot. 495+198+10=703=S(37) és megvagyunk! Megjegyzés: 1.tag=1 pont (0 szakasz/él), 2.tag=1+2=3 pont (1 szakasz/él), 3.tag=1+2+3=6 pont (2 szakasz/él), 4.tag=1+2+3+4=10pont (3 szakasz/él)...

Előzmény: [9] Gubbubu, 2004-01-06 21:44:46

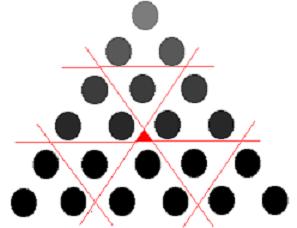
[9] Gubbubu

2004-01-06 21:44:46

Üdv! Itt mindenki alszik?

Talán felrázza ezt a fórumot a következő feladat (vagy az éberek maradéka is elalszik?)

Lehet, hogy ismerősek a háromszögszámok: az 1, az 1+2=3, az 1+2+3=6, stb., egyszóval az első n szám összege. E számok kirakhatóak szabályos háromszög alakban, ha az egységet mondjuk egy fekete pötty jelöli.

Jelölje e sorozat n-edik tagját S_n. Érvényes

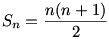
$S_n=\frac{n(n+1)}2$

Feladat: E sorozat 36-odik tagja 1+2+...+36=666, mint tudjuk, a Gonosz száma. Képzeljük el háromszög alakban pöttyökből (egységekből) kirakva! Osszuk a háromszög minden oldalát 3-3 egyenlő részre, és kössük össze a képzeletbeli osztópontokat: így 9 darab kisebb háromszög keletkezik, mindegyik oldala 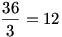$\frac{36}{3}=12$ egység hosszú. Ezért mindegyik kis háromszög S₁₂=78 db. egységet (pöttyöt) tartalmaz. Mivel 9 ilyen kis háromszög van, mindegyikben 78 pötty, szükségképpen

666=9*78=702

... Ajjaj! 666=702=666+36? Hát ezért 666 a Gonosz száma? (Feladat: hol a hiba a gondolatmenetben?)

[8] lorantfy

2003-12-23 12:35:33

Egy miniátverés:

Be fogjuk látni, hogy 1=2. Tegyük fel, hogy a=b.

Szorozzuk meg mindkét oldalt a-val: a²=ab.

Vonjunk ki mindkét oldalból b²-et: a²–b²=ab–b²

Bontsuk mindkét oldalt tényezőkre: (a+b)(a-b)=b(a-b)

Osszuk el mindkét oldalt (a - b) -vel: a+b=b.

Ha most még azt is feltesszük, hogy a =1, akkor 2 = 1.

[1] [2] [3]

Már regisztráltál?
Új vendég vagy?