| [1147] HoA | 2008-11-14 23:02:29 |
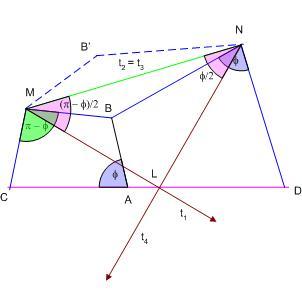
 A leírtak egészen az utolsó mondatig rendben vannak. Ha az utolsó mondatot mint egy itt nem részletezett bizonyítás eredményét tekintjük, akkor az is elfogadható. De önmagában nem. Természetesen ha KM és KN merőlegesek, akkor a rájuk történő tükrözések eredője egy 180 fokos forgatás, vagyis egy K pontra vonatkozó tükrözés. De hát éppen ezt a merőlegességet kéne bizonyítani. A [1146] -ban leírt forgatáshelyettesítésből nem következik, hogy éppen MK és NK lenne az a két egyenes, melyeket t1 -nek és t4 -nek választhatunk. Szerintem a [1146] -beli gondolat feladatunk megoldására az alábbiak szerint használható fel:
Az M körüli  - - szögű forgatás helyettesíthető két, egymással ( szögű forgatás helyettesíthető két, egymással ( - - )/2 szöget bezáró, t1ést2 egyenesre vett tükrözéssel. Válasszuk t2 -nek MN -t, és legyen t1 az ezzel -( )/2 szöget bezáró, t1ést2 egyenesre vett tükrözéssel. Válasszuk t2 -nek MN -t, és legyen t1 az ezzel -( - - )/2 szöget bezáró, M-en áthaladó egyenes. Hasonlóan az N körüli )/2 szöget bezáró, M-en áthaladó egyenes. Hasonlóan az N körüli  szögű forgatás helyettesíthető két, egymással szögű forgatás helyettesíthető két, egymással  /2 szöget bezáró, t3ést4 egyenesre vett tükrözéssel. Válasszuk t3 -nak MN -t, és legyen t4 az ezzel /2 szöget bezáró, t3ést4 egyenesre vett tükrözéssel. Válasszuk t3 -nak MN -t, és legyen t4 az ezzel  /2 szöget bezáró, N-en áthaladó egyenes. Legyen t1 és t4 metszéspontja L. A két forgatás eredője, vagyis a négy tükrözés eredője, mivel a t2 -re és t3 -ra vonatkozó tükrözés eredője azonosság, a t1 -re majd t4 -re végrehajtott tükrözés eredője. /2 szöget bezáró, N-en áthaladó egyenes. Legyen t1 és t4 metszéspontja L. A két forgatás eredője, vagyis a négy tükrözés eredője, mivel a t2 -re és t3 -ra vonatkozó tükrözés eredője azonosság, a t1 -re majd t4 -re végrehajtott tükrözés eredője.
Az MNL háromszögben az M-nél és N-nél lévő szögek összege 90o , ezért a háromszög L-nél derékszögű. Másrészt a tükrözések eredője egy L köröli 180o -os forgatás - L-re vonatkozó tükrözés - és mivel a forgatások eredője C-t D-be viszi, L = K. Ezzel már valóban bizonyítottuk, hogy MK és NK merőlegesek.
|
 |
| Előzmény: [1146] BohnerGéza, 2008-11-11 23:30:46 |
|
|
|
| [1144] HoA | 2008-11-10 11:43:00 |
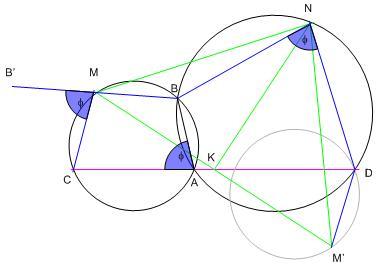
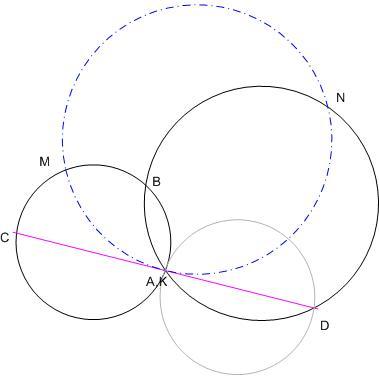
 A 141.feladat megoldása: Tükrözzük M-et K-ra, a tükörkép legyen M' .
a) Vegyük fel BM meghosszabbításaként az MB' = BM szakaszt. Jelöljük a BND szöget  -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is  . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja  -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja  -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
b) Felhasználjuk, hogy egy X pont körüli  szögű és egy Y pont körüli szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli szögű elforgatás eredője egy Z pont körüli  + + szögű elforgatás, speciálisan ha szögű elforgatás, speciálisan ha  + + = = , akkor egy Z pontra vonatkozó tükrözés. CMB szög = , akkor egy Z pontra vonatkozó tükrözés. CMB szög =  - - , az M körüli , az M körüli  - - szögű elforgatás C-t B-be viszi, az N körüli szögű elforgatás C-t B-be viszi, az N körüli  szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
|
 |
| Előzmény: [1143] BohnerGéza, 2008-11-05 23:18:14 |
|
| [1143] BohnerGéza | 2008-11-05 23:18:14 |
 A "kis segítség" önnálló feladatnak biztosan jó, ajánlom mindenkinek!
A 141. feladatra két megoldást ismerek, azokhoz nem használtuk ezt a segítséget, talán egy harmadikhoz jó.
Az általam ismett megodások alapszava:
- - - egyikhez: "ha felező..., akkor tükrözzünk rá!"
- - - másikhoz: "leképezések"
|
| Előzmény: [1142] HoA, 2008-11-05 11:24:39 |
|
|
| [1141] BohnerGéza | 2008-10-31 00:06:46 |
 A zalaegerszegi Zrínyi Miklós Gimnázium "IZSÁK IMRE GYULA" komplex természettudományi versenyének egyik szép feladatát ajánlom.
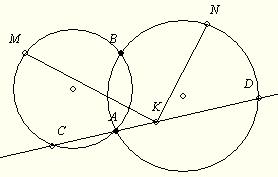
141. feladat: A k1 és k2 kör két pontban, A-ban és B-ben metszik egymást. Legyen C a k1-nek k2-n kívüli olyan pontja, melyre a CA egyenes k2-t olyan az A-tól különböző D pontban metszi, mely nincs a k1-en belül. Továbbá legyen K a CD, M a k1 A-t nem tartalmazó BC ívének és N a k2 A-t nem tartalmazó DB ívének felezőpontja. Bizonyítandó, hogy MKN szög derék!
|
 |
|
| [1140] HoA | 2008-10-26 23:06:36 |
 Pedagógiailag nagyon jó feladatnak tartom. Szinte vonzza a szemet, hogy AC felezőpontját E és G között NEM jelöli az F betü. Honnan ismerős a szakaszt két oldalról érintő két kör, ráadásul az ábra alapján a szakasz felezőpontjára szimmetrikus két pontban? Először belátjuk, hogy ez nem csak ránézésre van így, hanem a [1139] - beli egyenlőség éppen a feladat feltételeiből következik. És ami még "hiányzik" az ábráról: ABC beírt k1 körének E-vel átellenes H pontja - és ugyanígy ACD beírt k2 körének G-vel átellenes I pontja , melyek úgy tűnik, rajta vannak BG-n illetve DE-n. Végül az ABC háromszög AC oldalát G-ben érintő hozzáírt k3 kört megrajzolva teljes az ábra. Így már jól láthatóak a beírt és hozzáírt körök vizsgálatánál megismert hasonlóságok. k1 és k3 külső hasonlósági pontja B, ezért B, H és G valóban egy egyenesen van. k1 és k2 külső hasonlósági pontja P, ezért P, G és H egy egyenesen van. Vagyis P, G, H, B egy egyenes pontjai. És persze ugyanez áll P, D, I, E -re.
|
| Előzmény: [1134] BohnerGéza, 2008-10-12 01:13:22 |
|
|
| [1138] HoA | 2008-10-20 08:50:44 |
 Két előzetes megjegyzés:
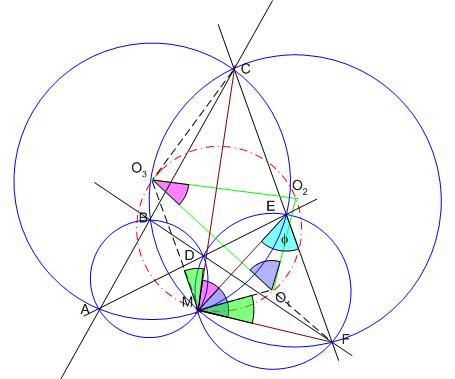
1) Nem nyilvánvaló kapcsolatot találni egy ábra bizonyos pontjain átmenő körök középpontjai és az ábra többi része között. Az itt célravezető meglátás: két egymást metsző kör centrálisa merőleges a közös húrra. Ezt a bizonyításban többször is felhasználjuk.
2) Ha sikerül bebizonyítnai, hogy tetszőleges három körülírtkör-középpont a körülírt körök közös M pontjával egy körön van, akkor egyúttal azt is bizonyítottuk, hogy a négy körülírt kör középpontja és M egy körön van, hiszen például ha O1,O2,O3ésM egy körön van , valamint O1,O2,O4ésM egy körön van, akkor ez úgy is fogalmazható, hogy O3ésO4 is rajta van az O1,O2 és M ponthármas által meghatározott körön.
[1136] ábráját megbetűzve MF merőleges O1O2 -re, ME merőleges O1O3 -ra , így nem egymás szögtartományába eső merőleges szárú szögek lévén FME =O2O1O3 =O2O1O3 . Hasonlóan adódik, hogy EMC . Hasonlóan adódik, hogy EMC =O1O3O2 =O1O3O2 . A kettőt összegezve FMC . A kettőt összegezve FMC O3O2O1 O3O2O1 kiegészítő szögével egyenlő. kiegészítő szögével egyenlő.
Jelöljük az MEF -et -et  -vel. Az O1 középpontú k1 körben ez az MF húrhoz tartozó kerületi szög. MFO1 egyenlőszárú -vel. Az O1 középpontú k1 körben ez az MF húrhoz tartozó kerületi szög. MFO1 egyenlőszárú  -ben -ben  a középponti szög, MO1F a középponti szög, MO1F fele, így FMO1 fele, így FMO1 = = /2- /2- . .
Az O3 középpontú k3 körben CEM = = - - a rövidebbik CM ívhez tartozó kerületi szög, a hosszabbik CM ívhez tartozó kerületi szög a rövidebbik CM ívhez tartozó kerületi szög, a hosszabbik CM ívhez tartozó kerületi szög  , az MCO3 egyenlőszárú , az MCO3 egyenlőszárú  -ben -ben  a középponti szög, MO3C a középponti szög, MO3C fele, így CMO3 fele, így CMO3 = = /2- /2- . .
O1MO3 =FMC =FMC -FMO1 -FMO1 +CMO3 +CMO3 =FMC =FMC , az O3O2O1 , az O3O2O1 kiegészítő szöge, tehát O1,O2,O3ésM egy körön vannak. kiegészítő szöge, tehát O1,O2,O3ésM egy körön vannak.
|
 |
| Előzmény: [1136] BohnerGéza, 2008-10-16 19:03:53 |
|
|
|
| [1135] BohnerGéza | 2008-10-12 01:28:32 |
 140/b feladat: Bizonyítandó, ha a 140. feladatban az ABCD négyszög konkáv, akkor az állítás - ha vannak - a közös belső érintőkkel, igaz! ( Szóval a BG és DE átmegy a körök belső hasonlósági pontján. )
Megjegyzés: Ha a 140-ben a két kör sugara egyforma, akkor BG és DE párhuzamos a centrálisukkal.
|
| Előzmény: [1134] BohnerGéza, 2008-10-12 01:13:22 |
|
| [1134] BohnerGéza | 2008-10-12 01:13:22 |
 140.feladat: A konvex ABCD négyszögben DA+AB=BC+CD-vel. (Nem érintőnégyszög!) Az ABC háromszög beírt köre érintse AC-t az E, a BDA-é a G pontban. Bizonyítandó, hogy a beírt körök közös külső érintői, a BG és a DE egyenesek egy ponton mennek át!
|
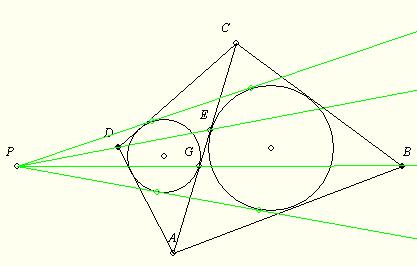 |
|
| [1133] sakkmath | 2008-10-05 16:13:09 |
 Kérdéseddel dr. Dályay Pál Péterhez, a szegedi Deák Ferenc Gimnázium tanárához célszerű fordulni. A feladatot az ő javaslatára a The American Mathematical Monthly tűzte ki 2006-ban 11240-es sorszámmal. A 2008. évi februári szám internetes hivatkozása itt már a rövidített megoldást is közli.
|
| Előzmény: [1132] Lóczi Lajos, 2008-10-03 21:21:38 |
|
| [1132] Lóczi Lajos | 2008-10-03 21:21:38 |
 Az exponenciális függvény konvexitása miatt minden valós x-re 1+x ex. Speciálisan, ha x ex. Speciálisan, ha x (0,1), akkor 1-x (0,1), akkor 1-x e-x, így e-x, így 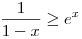 . Legyen most . Legyen most 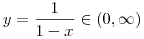 tetszőleges, ekkor tetszőleges, ekkor 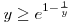 . Végezzük itt el az . Végezzük itt el az 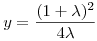 helyettesítést, ha helyettesítést, ha  >0 tetszőleges. Azt kapjuk, hogy >0 tetszőleges. Azt kapjuk, hogy 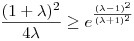 . Legyen most . Legyen most 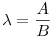 , ha A>0 és B>0 tetszőleges. Ekkor , ha A>0 és B>0 tetszőleges. Ekkor 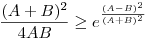 . Ha C>0 tetszőleges, akkor betűcserével ebből azt kapjuk, hogy . Ha C>0 tetszőleges, akkor betűcserével ebből azt kapjuk, hogy 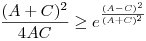 és és 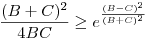 is igaz. Az utolsó három egyenlőtlenséget összeszorozva azt nyerjük, hogy minden pozitív A, B és C-re is igaz. Az utolsó három egyenlőtlenséget összeszorozva azt nyerjük, hogy minden pozitív A, B és C-re
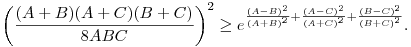
Vonjunk gyököt az egyenlőtlenségből, majd végezzük el az A=a+b-c>0, B=a-b+c>0, C=-a+b+c>0 helyettesítéseket, ahol a, b és c a háromszög oldalai. Azt kapjuk, hogy
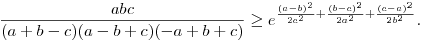
A fenti bal oldal viszont éppen  . .
Amúgy honnan jött ez az állítás? (Valami hiperbolikus/abszolút geometriai tétel?)
|
| Előzmény: [1131] sakkmath, 2008-10-03 13:36:48 |
|
|
| [1130] Káli gúla | 2008-10-01 16:36:48 |
 Ha K a a háromszög symmediáns pontja és O a köré írt kör középpontja, akkor a Tucker körök középpontjai éppen az OK szakasz pontjai. A bizonyítás megtalálható pl. W. Mclelland: A Treatise On The Geometry Of The Circle. Macmillan, 1891. könyvében a 73. oldalon. A könyv olvasható, és le is tölthető a www.archive.org oldalon, csak rá kell keresni a címére.
|
| Előzmény: [1128] klerox, 2008-09-30 17:45:13 |
|
|
| [1128] klerox | 2008-09-30 17:45:13 |
 A Tucker körnek a lényege: Feltétel: A'A"=B'B"=C'C", és A'A", B'B" és a C'C" antiparallel a BC, CA és AB oldalakkal. A hat pont: A', A", B', B", C' és C" egy körön helyezkedik el. Tudomásom szerint kell középpontjának lenni.
|
|
| [1127] BohnerGéza | 2008-09-29 22:40:25 |
 Biztos, hogy nem a "Matematikus-fizikus viccek, sztorik" közé akartad írni?
Utána néztem, a Tucker-kör vszleg hatszög, azaz önmagába visszatérő vonal. Ilyet a talpponti háromszög (piros) segítségével is meg lehet szerkeszteni. Az ábrán kettő látszik (kék, zöld) és nyilván végtelensok van. Mivel ezen hatszögek köré írható kör, de ezek kp-jai nem esnek egybe, nincs értelme a kérdésnek.
|
 |
| Előzmény: [1126] klerox, 2008-09-29 19:30:34 |
|
| [1126] klerox | 2008-09-29 19:30:34 |
 Sziasztok!
A Tucker-kör megszerkesztésével bajlódok, de sehogy nem jövök rá a középpont megszerkesztésére, kérlek segítsetek.
Előre is köszönöm
|
|
| [1125] BohnerGéza | 2008-09-24 11:16:44 |
 Ismert a következő: Ha négy egyenes négy háromszöget határoz meg, akkor ezek körülírt körei átmennek egy közös ponton.
138. feladat: Bizonyítandó, hogy a négy körülírt kör középpontja és ez a közös pont egy körön van.
|
|
|
| [1122] Sirpi | 2008-09-08 13:41:42 |
 Nemrég nekem is szükségem volt hasonló programra, csak éppen gömbközéppontot kellett keresni felületi pontok alapján, és írtam egy egyszerű módszert, ami a tesztek alapján elég jól működik, röviden le is írom, hogyan (körre is jó változtatás nélkül):
Legyenek adva a P1,P2,...,Pn pontjaink, és keressük az O középpontot iterációs módszerrel. Legyen O0 a megadott Pi ponthalmaz súlypontja. Ha egyenletes a ponteloszlás, akkor ez már önmagában is majdnem jó, de ha nem, akkor is egy jó kiindulópont.
Nézzük a k+1. lépést: rendezzük sorba a Pi pontokat az Ok-tól vett távolság alapján, és a robusztusság miatt ebből hagyjuk el a legközelebbi és a legtávolabbi 10%-ot, legyen ez első meghagyott pont R (tehát ez egy majdnem legközelebbi pont Ok-hoz képest), az utolsó S (ez pedig a majdnem legtávolabbi, leszámítva a felső 10%-ot). Ideális esetben Ok-t az RS szakasz felezőmerőlegesére kellene "ráhúzni", de tapasztalataim alapján így lassabb a konvergencia, mintha csak a felezőmerőlegeshez képest a felére csökkentenénk a távolságot. Tehát ha Ok talppontja RS felezőmerőlegesére T, akkor Ok+1-nek válasszuk Ok és T felezőpontját, majd folytassuk az eljárást.
Megállási feltétel: Egy adott Ok pont jóságát mérjük az |SOk|-|ROk| különbséggel, és ha ez kisebb, mint az eddigi legjobb, akkor jegyezzük meg ezt, mint lehetséges végső kör/gömbközéppontot. És ha mondjuk 1000 iterációs lépésen keresztül ez a rekord nem dől meg, akkor legyen ez a végső győztes is egyben.
|
| Előzmény: [1121] farkasb, 2008-09-08 00:49:03 |
|



 -
- szögű forgatás helyettesíthető két, egymással (
szögű forgatás helyettesíthető két, egymással (


 szögű és egy Y pont körüli
szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli
szögű elforgatás eredője egy Z pont körüli 

 =O2O1O3
=O2O1O3 -ben
-ben 




 ex. Speciálisan, ha x
ex. Speciálisan, ha x (0,1), akkor 1-x
(0,1), akkor 1-x >0 tetszőleges. Azt kapjuk, hogy
>0 tetszőleges. Azt kapjuk, hogy 



