|
| [1227] Editkesss | 2009-05-17 09:10:21 |
 Köszönöm szépen a segítséget! :) De lenne még egy-két feladatom! Az első: Tetszőleges e egyenes esetén jelölje: "Te" az e-re való tükrözést. Mutassuk meg, hogy ha "a" és "b" párhuzamos egyenesek, továbbá TaTbTcTaTbTc= identitás, akkor "c" is párhuzamos a-val és b-vel.
Második: Mutassuk meg, hogy ha az A1A2A3A4 és B1B2B3B4 négyszögek paralelogrammák, az AiBi szakasz Ai-hez legközelebbi negyedelőpontja Ni (i=1,2,3,4), akkor az N1N2N3N4 négyszög is (esetleg elfajuló) paralelogramma.
Előre is köszönöm!:)
|
|
| [1226] Euler | 2009-05-16 22:21:09 |
 A feladatot megpróbálom általánositva megoldani, vegyünk két nem egybeeső pontot, ekkor keressük azt a pontot a sikon, amelytől vett távolságaik négyzetösszege minimális, könnyen ellenőrizhető, hogy pont a két pontot összekötő szakasz felezőpontja lesz, pl. koordinátageometriával könnyen kijön,legyen A(a1;a2), B(b1;b2), a keresett pont: P(x;y), innen már csak egy másodfokú kifejezésnek kell vizsgálni a szélsőértkét, adódik az eredmény.Ez máshogy is kijöhet, bár itt nem biztos, hpogy "érdemes" igy gondolkodni, de ha mégis igy tesszük, akkor könnyen általánositható a probléma. Tudjuk ugyanis azt, hogy bármely háromszögben a szokásos jelölésekkel: 4sc2=2a2+2b2-c2(ez elég ismert összefüggésnek tekinthető,remélem.),a PAB háromszögre ezt felirva, kapjuk, hogy akkor lesz minimális a négyzetösszeg, ha a felezőponttól vett távolság minimális, máris adódik az eredmény. Kicsit továbblépve, vegyünk egy háromszöget(az egyszerűség kedvéért nem elfajulót), legyenek a csúcsai:A(a1;a2), B(b1;b2), C(c1;c2). keressük azt a pontot a sik egy adott egyenesén , amelytől vett távolságnégyzetösszeg minimális. Itt is hasonlóan eljárva, ráhúzodik a súlypontra az, ami előbb a felezőpontra húzodott rá,emiatt pedig az egyenesen lévő merőleges vetülete lesz a megfelelő pont.(Remélem érthető).Eljutottunk a Te problémádhoz, innen már "könnyű" elbánni vele, hiszen tekintsük az EBA és ECD háromszögeket, adódik, hogy akkor lesz mionimális a négyzetösszeg, ha az E-nek a CD és AB oldalak feletzőpontjától vett négyzetösszeg minimális, ez pedig használva az előzőeket, pontosan akkor lesz, ha a két felezőpont felezőpontjától vett távolság minimális, ez a pont pedig éppen a tetraéder súlypontja, ezt pl. vektorokkal lehet igazolni nagyon könnyen, igy itt a súlypontot kell merőlegesen vetiteni a sikra, ez lesz a keresett pont. Nyilván ha emeljük a dimenziószámot, hasonlóan adódik a feladat megoldása, csak maximum nem tudjuk elképzelni, hogy miről is szól a feladat. :-) remélem, tudtam segiteni a probléma megértésében.
|
| Előzmény: [1225] Editkesss, 2009-05-16 18:57:42 |
|
| [1225] Editkesss | 2009-05-16 18:57:42 |
 Hello, nekem egy olyan feladatom lenne, hogy adva van egy S sík és egy abcd tetraéder. veszünk egy E pontot . kérdés: Az S sík mely E pontjára lesz ez AE*2+BE*2+CE*2+DE*2 a kifejezés értéke a legkisebb? *2 a négyzetet jelöli!
|
|
|
| [1223] Vonka Vilmos Úr | 2009-05-15 15:46:44 |
 Akkor tényleg csak néhány ötlet:
1. és 2. Az adott ponton keresztül, amelynek a képét keressük, tekintsünk egy tetszőleges segédegyenest, és próbáld először ennek a képét megszerkeszteni.
3. A megfelelő egyenespár segítségével először határozzuk meg a kollineáció tengelyét, majd használjuk ki azt a tényt, hogy a centrum és az eltűnési egyenes távolsága megegyezik a tengely és az ideális egyenes képének távolságával.
4. A megfelelő egyenespár és egy pont ismeretében ismét először keressük meg a tengelyt. Majd válasszunk egy tetszőleges segédpontot azon az egyenesen, amelyiknek adott a képe; és próbáld a választott pont képét megszerkeszteni.
5. Az ABCD négyszög képe akkor lesz paralelogramma, ha a szemköztes oldalegyenesek metszéspontjaihoz a kollineáció ideális pontot rendel. Ez alapján határozd meg először az eltűnési egyenest. A tengely meghatározásához pedig tekintsünk ismét egy segédegyenest azon a ponton keresztül, amelynek a képe adott, és szerkesszük meg először a segédegyenes képét.
Remélem, innentől már menni fog!
|
| Előzmény: [1218] kandi, 2009-05-13 07:55:44 |
|
| [1222] kandi | 2009-05-15 10:42:38 |
 Köszönöm a linket, bár nem igazán értem az anyagot:( Amúgy centrális kollineációval oldhatók meg elvileg a feladatok és mi a projektív geometriával foglalkozunk. Ha mégis lenne még egy kis segítség mert én már kifuladtam a sz ötletekből?!
|
|
| [1221] jonas | 2009-05-14 21:55:55 |
 Én inkább ábrázoló geometriára tippelnék, bár szerencsére nekem nem kellett ilyesmit tanulnom, úgyhogy nem vagyok biztos, hogy valóban erről van szó.
|
| Előzmény: [1219] HoA, 2009-05-14 15:22:08 |
|
| [1220] HoA | 2009-05-14 16:14:44 |
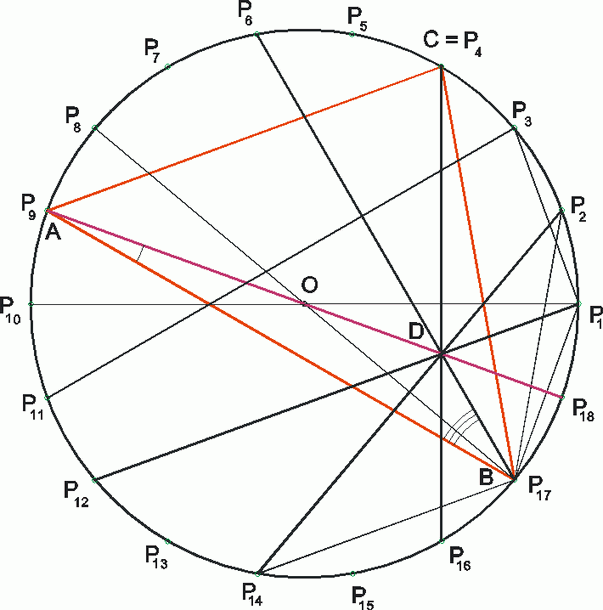
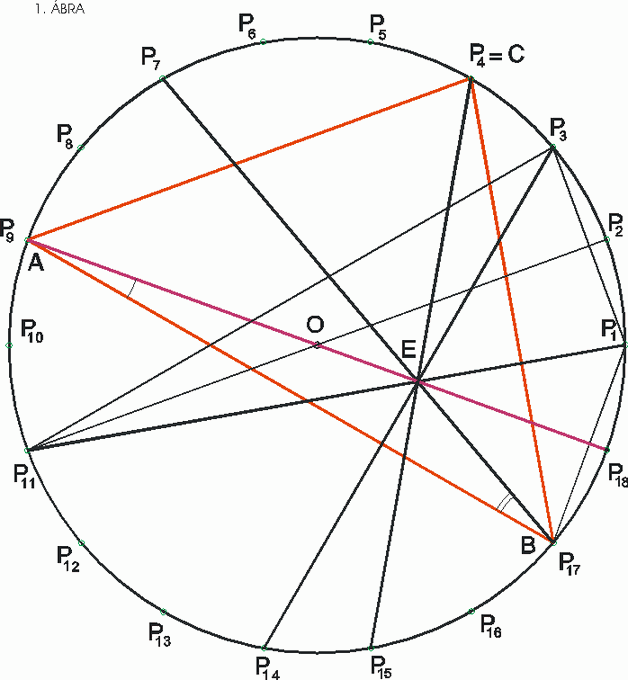
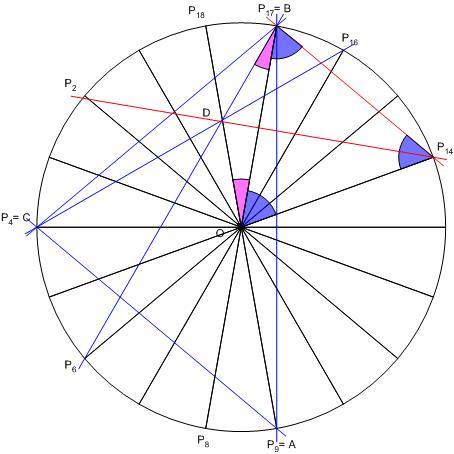
 Gratulálok! Igen, erre a megoldástípusra gondoltam! A D ponthoz tartozó bizonyításra egy másik változat: A definíció szerint D a P9P18 és P6P17 átlók metszéspontja, és azt kell igazolni, hogy P4P16-on is rajta van. DBO =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD =20o ,mint a P17P18 ívhez tartozó középponti szög, OBD =20o ,mint a P17P18 ívhez tartozó középponti szög, OBD egyenlőszárú. P14OP17 egyenlőszárú. P14OP17 =60o ( 3 ívegység középponti szöge ) , P14OP17 =60o ( 3 ívegység középponti szöge ) , P14OP17 szabályos. Így BDOP14 deltoid, P17P14D szabályos. Így BDOP14 deltoid, P17P14D =30o . Így D rajta van a P14P17-tel 30o-ot bezáró P2P14 átlón és ennek P9P18 -ra vett tükörképén, P4P16-on is. =30o . Így D rajta van a P14P17-tel 30o-ot bezáró P2P14 átlón és ennek P9P18 -ra vett tükörképén, P4P16-on is.
|
 |
| Előzmény: [1216] sakkmath, 2009-05-12 15:24:47 |
|
| [1219] HoA | 2009-05-14 15:22:08 |
 Szia Kandi! Ez itt a KöMaL Geometria fóruma. Feladataid úgy látom, nem egészen a középiskolai geometria témájába tartoznak, ami még önmagában nem baj. Csak az nem világos, miről is van szó. A használt fogalmak alapján úgy gondolom, valamilyen projektív geometriai kurzusra jársz. A feladatok esetleg mind centrális kollineáció témába esnek? Ha nem ismered, talán segít ez a jegyzet:
http://www.jgytf.u-szeged.hu/~krisztin/projektiv.doc
|
| Előzmény: [1218] kandi, 2009-05-13 07:55:44 |
|
| [1218] kandi | 2009-05-13 07:55:44 |
 Szia Mindenki! Én még itt új vagyok, úgyhogy nem nagyon tudom, hogy hogyan működik, de nagy segítségre lenne szükségem. Van 5 db szerkesztési példám. Ami elvileg nagyon könnyű, de én nem tudtam megcsinálni, ha valaki segítene megköszönném. Leírom a feladatokat: 1., adott : tengely, centrum, eltűnési egyenes.Szerk. meg tetszőleges pont képét! 2., adott : tengely, centrum, ideális egyenes képe.Szerk. meg tetszőleges pont képét! 3., adott : az eltűnési egyenes, az ideális egyenes képe, és egy egymásnak megfelelő egyenespár.Szerk. meg a centrumot és a tengelyt! 4., adott : egy megfelelő pontpár, egy megfelelő egyenespár és a tengely egy pontja. Szerk. meg a centrumot és a tengelyt! 5., adott : a centrum és egy megfelelő pontpár. Határozzuk meg a tengelyt úgy, hogy egy előre adott ABCD négyszög képe paralelogramma legyen! Előre is köszönöm:)
|
|
| [1217] MTM | 2009-05-12 18:06:51 |
 151.feladat:
ABC háromszög körülírt körét, AB és AC oldalt rendre D, E, G-ben érinti egy kör. Bizonyítsuk be, hogy BDC szög felezője felezi EG szakaszt.
|
|
|
|
|
| [1213] sakkmath | 2009-05-12 15:20:18 |
 A HoA [1208]-as hozzászólásában kitűzött 150. feladat két feladatnak tekinthető. Elnézést, de sajnos csak négy részletben tudom feltenni a megoldást: a képek 50 KB-os határával a megfelelő képminőség ugyanis nem összeegyeztethető.
A megoldás 1. része:
|
 |
| Előzmény: [1208] HoA, 2009-04-29 15:00:17 |
|
|
| [1211] BohnerGéza | 2009-05-11 23:22:32 |
 Segítség a 150. feladat egy lehetséges megoldásához: Az E és D pontot máshogy definiálva lássuk be addíciós tételek következménye segítségével, hogy megfelelnek az eredeti definíciónak.
Egyelőre megpróbálok más jellegű (számomra szebb) megoldást is kitalálni.
|
| Előzmény: [1208] HoA, 2009-04-29 15:00:17 |
|
| [1210] HoA | 2009-05-07 22:43:48 |
 Mit néztél el? Szerintem a feladat jó. Nyilván sokunknak beugrik a hetedik, azonos sugarú kört és egymást érintő hat kör, és ezek befoglaló köre. De azt nem sikerült bizonyítanom, hogy a hetedik kör elhagyásával nem adható jobb megoldás - kisebb befoglaló kör.
|
| Előzmény: [1209] BohnerGéza, 2009-05-07 00:35:55 |
|
|
|
| [1207] BohnerGéza | 2009-04-17 13:56:24 |
 A 149. feladathoz: 2. rész.
Az előző [1206] hozzászólás folytatása.
A megoldásban nem törekedtem a teljességre, a legegyszerűbb megfogalmazásra, inkább a gondolatmenet bemutatására.
Jó lenne, ha valaki szebben megfogalmazott, vagy más jellegű megoldást is adna!
Vegyük észre a kapcsolatot az itt és HoA[1204] hozzászólásában látottak közt!
|
 |
| Előzmény: [1206] BohnerGéza, 2009-04-17 13:43:59 |
|
| [1206] BohnerGéza | 2009-04-17 13:43:59 |
 A 149. feladathoz: 1. rész.
Folytatása a következő hozzászólásban.
|
 |
|
| [1205] BohnerGéza | 2009-04-17 13:29:51 |
 Nekem is hiányérzetem volt janomo[1200] hozzászólásával kapcsolatban. Igaz így legalább HoA pontos, érthető megfogalmazásában láthattuk a megoldást!
Példát mutatok egy kevésbé szépre a következő hozzászólásban, az eredeti feladat kapcsán. Remélem, látható lesz belőle, hogy a szép megoldások is esetleg hosszabb gondolkodás után, sok munka árán, nem véletlenszerűen jönnek össze. Az így elért eredmény, sőt részeredmény is örömet adhat. (Ráadásul nem kell közben pl. négykerekű motoros marhasággal -nem jut eszembe a neve - tönkretenni a környezetet.)
149. feladat: A Surányi János emlékverseny 2. feladata: Az ABC háromszög beírt köre az AB és AC oldalakat rendre a D és E pontban érinti. A beírt körnek és az AEB háromszög köré írt körnek E-től különböző közös pontja legyen F, a D pont merőleges vetülete az EB egyenesen G. Igazoljuk, hogy 2ABEszög=BFGszög.
(Elnézést, a továbbiakban ezeket az eredeti jelöléseket használom!)
|
| Előzmény: [1204] HoA, 2009-04-17 09:10:46 |
|
| [1204] HoA | 2009-04-17 09:10:46 |
 Szerintem nem érdemes annyival elintézni az inverziós megoldást, hogy „inverzió a B pontra és kész”. Más feladatoknál is felhasználható például, hogy három, a póluson nem áthaladó egyenesen fekvő pont képe egy, a póluson átmenő körön van, és viszont: ha négy pont húrnégyszöget alkot – egy körön van – akkor egyiküket pólusnak választva a másik három pont inverz képe egy egyenesen fekszik.
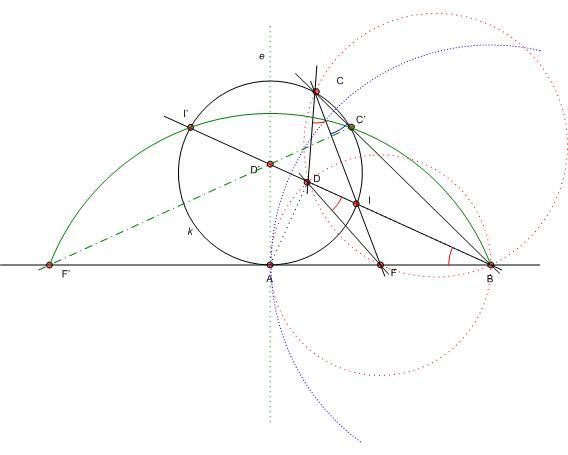
Legyen tehát az inverzió pólusa B, alapköre a k-t merőlegesen metsző kör. Ekkor k képe önmaga, A és A’ egybeesik, F képe az AB egyenes F’ pontja, melyre F’A = AB, AB Thálesz-körének képe az AB-re merőleges e egyenes, D képe, D’ BD és e metszéspontja, I képe a BI egyenes k-val alkotott második metszéspontja. CIF egyenes képe a B’, F’, I’ pontok által meghatározott kör. Ennek F’B húrja, e húrfelező merőlegese, tehát szimmetriatengelye. e k-nak is szimmetriatengelye, így a két kör metszéspontjai, C’ és I’ egymás tükörképei e-re. Ez igaz az F’, B pontpárra is, tehát a BD’I’ egyenes e-re vett tükörképe az F’D’C’ egyenes. A fentiek szerint ezért BCDF húrnégyszög, körülírt körében az egyenlő BF és DF húrokhoz egyenlő kerületi szögek tartoznak: DCF =FCB =FCB . .
|
 |
| Előzmény: [1200] janomo, 2009-04-04 12:18:33 |
|






 =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD
=20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD egyenlőszárú. P14OP17
egyenlőszárú. P14OP17