| [1355] sakkmath | 2010-01-06 16:51:48 |
 A következő feladatomat ajánlom megoldásra. (A megoldás végén valószínűleg elkerülhetetlen lesz számítógépes program használata. Ha ezért kissé kilógna e topicból, elnézést ... .)
(Kb.) 162. feladat: Egy hegyesszögű, nem egyenlő szárú háromszög területe T, oldalainak hossza a, b és c. A háromszög valamennyi magassági talppontján át húzzunk párhuzamost a talpponti oldallal szemközti csúcs szögfelezőjével. Tekintsük az így kapott egyeneseknek a szögfelező egyenesekkel alkotott metszéspontjait. Bizonyítsuk be, hogy e pontok két egyenlő területű háromszöget határoznak meg, melyek t1, illetve t2 nagyságú területére:
|
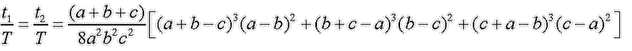 |
|
|
| [1353] laci777 | 2010-01-05 22:59:40 |
 Hát igen... Nekem meg épp ez a feladat volt elsőre (meg másodikra is...:P) megoldhatatlan.
Azért szerintem a túlzott szerénységre nincs okod:)
Köszönöm és további szép estét: Laci
|
| Előzmény: [1352] SmallPotato, 2010-01-05 22:47:32 |
|
|
|
| [1350] laci777 | 2010-01-05 22:43:06 |
 Kedves SmallPotato!
Nagyon szépen köszönöm az elegáns megoldást - bár lehet, itt ez a példa nem lehetett komolyabb kihívás.
Nem vettem észre a hasonló háromszögeket (sem)...
Még egyszer köszönöm!
További szép estét, szia: Laci
|
| Előzmény: [1348] SmallPotato, 2010-01-05 22:15:41 |
|
| [1349] HoA | 2010-01-05 22:31:51 |
 Ja, az más. Ha biztosra akarsz menni, használd [1343] lépéseit. Vagy kérdezd meg [1341] szerzőjét, ő hogy jutott erre az eredményre.
|
| Előzmény: [1346] Tym0, 2010-01-05 21:17:10 |
|
|
| [1347] SmallPotato | 2010-01-05 22:09:51 |
 Rajzold fel az elrendezésnek a kúp tengelyén átmenő síkmetszetét. Rajzold be a gömb két sugarát: a kúp alapkörének középpontjába irányulót és az alkotóra merőlegest. Az ábrádon két hasonló derékszögű háromszög lesz: az egyiknek a befogói a kúp alapkörének sugara és a kúp magassága, a másiknak a befogói az alkotóra merőlegesen berajzolt gömbsugár és az alkotónak a kúp csúcsa felé eső szelete. Írd fel a befogók arányát mindkét háromszögben.
|
| Előzmény: [1342] laci777, 2010-01-05 19:41:20 |
|
| [1346] Tym0 | 2010-01-05 21:17:10 |
 Bocs de nekem nincs se időm se türelmem bizonyítani. Én biztosra akarok menni. Elkezdtem csinálni. egyébként mástól kaptam. Remélem jó lesz.
|
| Előzmény: [1345] HoA, 2010-01-05 21:15:15 |
|
| [1345] HoA | 2010-01-05 21:15:15 |
 Nem tudom, nem számoltam végig. Ha a [1341]-ben leírtakat saját magad találtad ki, nyilván tudod, miért. Ha mástól vetted át, akkor dolgozz egy kicsit: bizonyítsd vagy cáfold [1343] utolsó képletét.
|
| Előzmény: [1344] Tym0, 2010-01-05 20:26:30 |
|
| [1344] Tym0 | 2010-01-05 20:26:30 |
 Na most megint jól bekavartál. CSak annyit mondj hogy jó az amit az 1341-es hozzászólásomban írtam. Úgy kijön az általam keresett megoldás?
|
| Előzmény: [1343] HoA, 2010-01-05 19:55:45 |
|
| [1343] HoA | 2010-01-05 19:55:45 |
 Ismert, hogy a háromszög körülírt körének K középppontját a csúcsokból álló pontrendszer súlypontjaként úgy tudjuk előállítani, hogy a csúcsokat a megfelelő szögek kétszeresének sinusával súlyozzuk. Lásd pl. Reiman István: Geometria és határterületei:
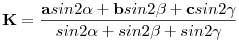
[1341]-ben a1,a2,a3 a (sík)háromszög oldalhosszainak négyzetei, a b1,b2,b3 súlyok a háromszög oldalait hagyományosan a,b,c-vel jelölve az
a2(b2+c2–a2),b2(c2+a2–b2),c2(a2+b2–c2)
mennyiségek. x,y,z a csúcsok ilyen súlyokkal vett súlypontjának koordinátái. Az nem baj, hogy a súlyok összege nem 1, és így a súlypont nincs a háromszög síkjában, mert az utolsó képlettel úgyis a gömbre vetíted. A megoldás akkor helyes, ha be tudod bizonyítani, hogy a súlyok aránya megfelelő, vagyis például
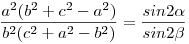
|
| Előzmény: [1341] Tym0, 2010-01-05 18:27:01 |
|
| [1342] laci777 | 2010-01-05 19:41:20 |
 Sziasztok, és b.ú.é.k. mindenkinek!
A Geometriai feladatok gyűjteménye I. 2776-os feladata sajnos megfogott. Tudna valaki segíteni benne? A feladat: Adott R sugarú gömbk köré írjunk olyan egyenes körkúpot, hogy térfogatának és a gömb térfogatának aránya adott k legyen. Határozzuk meg a kúp alapkörének a sugarát (r-t).
Addig jutottam, hogy r négyzet*m = 4*R köb*k (azaz gyakorlatilag semeddig), de a körkúp magassága (m), alkotója és sugara kívánatos aránya már kifogott rajtam.
Minden segtséget előre is köszönök! Sziasztok: Laci
|
|
| [1341] Tym0 | 2010-01-05 18:27:01 |
 Ehhez mit szóltok? Vagy ez ugyanaz amit ti mondtatok? Szerintem ez jó lesz. Szerintetek?
A gömb középpontja legyen az origó, a gömb sugara legyen R.
A kiindulási pontok a gömbön legyenek (x1,y1,z1), (x2,y2,z2), (x3,y3,z3).
Sorra számold ki az alábbi mennyiségeket:
a1 := (x2-x3)2 + (y2-y3)2 + (z2-z3)2
a2 := (x3-x1)2 + (y3-y1)2 + (z3-z1)2
a3 := (x1-x2)2 + (y1-y2)2 + (z1-z2)2
b1 := a1*(a2+a3-a1)
b2 := a2*(a3+a1-a2)
b3 := a3*(a1+a2-a3)
x := b1*x1 + b2*x2 + b3*x3
y := b1*y1 + b2*y2 + b3*y3
z := b1*z1 + b2*z2 + b3*z3
c : = R/gyök(x2+y2+z2)
A gömbön a körülírt kör középpontjának keresett koordinátái (c*x,c*y,c*z).
|
| Előzmény: [1340] HoA, 2010-01-05 11:40:36 |
|
| [1340] HoA | 2010-01-05 11:40:36 |
 Az eddigiek alapján a lépések:
-Adottak A, B, és C földrajzi koordinátái, északi szélesség =  , keleti hosszúság = , keleti hosszúság = 
-Átszámítjuk Descartes-koordinátákba : Pz=sin ;Px=cos ;Px=cos ,Py=sin ,Py=sin ( P = A,B,C ) ( P = A,B,C )
-Válasszuk úgy a jelölést, hogy ABC pozitív körüljárású  legyen legyen
-Képezzük az N = (B-A) x (C-A) vektorszorzatot, ez a gömb középpontjából kifelé mutat.
-A keresett középpont földrajzi koordonátáit az előzőek alapján kapjuk: sin  =Nz/|N| , tg =Nz/|N| , tg  =Ny/Nx =Ny/Nx
|
| Előzmény: [1334] Tym0, 2010-01-04 22:31:59 |
|
| [1339] HoA | 2010-01-05 11:14:08 |
 „Mindenkinek” igaza van, függetlenül attól, hogy gömbi vagy Descartes koordinátákat használunk.
-a gömb 3 különböző pontja, mint 3 térbeli pont, meghatároz egy S síkot
-ez a sík a gömböt egy körben metszi, és mivel a 3 pont a síkon is és a gömbön is rajta van, ez a kör éppen a 3 pont által meghatározott háromszög körülírt köre
-A BohnerGéza által javasolt vektorszorzat S (egy) N normálvektora, tehát S-re merőleges.
-A gömb középpontjából a gömböt metsző S síkra bocsátott N merőleges S –et a gömb és S metszésvonalát képező kör középpontjában döfi ( szimmetria ) . Talán ez hiányzott a leírtakhoz.
-N a gömböt abban a pontban metszi, amelyik egyenlő távolságra van a 3 adott ponttól – a földgömbnek ebbe a ponjába beszúrt körzővel a 3 ponton áthaladó kört lehet rajzolni
-A körközéppont földrajzi koordinátáinak meghatározásához N hossza lényegtelen. A Descartes koordinátáknak csak itt van szerepe. Ha a földrajzi szélességet  -vel, a hosszúságot -vel, a hosszúságot  –val jelöljük, akkor sin –val jelöljük, akkor sin  =Nz/|N| , tg =Nz/|N| , tg  =Ny/Nx =Ny/Nx
|
| Előzmény: [1338] sakkmath, 2010-01-05 09:59:14 |
|
| [1338] sakkmath | 2010-01-05 09:59:14 |
 Szerintem Jonasnak (1328) igaza van akkor, ha a gömbháromszög csúcsai euklideszi koordinátákkal adottak.
Ha viszont az adott koordináták gömbi, földrajzi koordináták, akkor az eddigi hozzászólások nem érvényesek, ugyanis a többi hozzászóló is euklideszi koordinátarendszerben gondolkodott.
|
| Előzmény: [1336] Tym0, 2010-01-05 01:38:08 |
|
|
| [1336] Tym0 | 2010-01-05 01:38:08 |
 Ez mind oké. De foylton síkot említesz. Egy gömfelületen levő háromszög nem lehet sík hiszen a gömbnek a felületén van. Vagy én vagyok a hülye és én nem értem...
|
| Előzmény: [1335] BohnerGéza, 2010-01-04 23:08:22 |
|
|
| [1334] Tym0 | 2010-01-04 22:31:59 |
 A lépéseket próbáld meg leírni lécci. Most ott tartok hogy van 3 (a háromszög csúcspontjai) + 3 (a háromszög oldalainak felezőpontjai) koordinátapontom (amik ugye x,y,z koordináták mert térről beszélünk). És ugye a göm középpontjának koordinátja ami ugye x,y,z alakban 0,0,0. Ezután mi jön? Mik a lépések?
|
|
|
| [1332] BohnerGéza | 2010-01-04 21:14:01 |
 Mivel egyforma húrokhoz egyforma gömbi távolságok tartoznak:
Térben a három ponttól egyenlő távolságra lévő pontok halmaza: a háromszög körülírt körének középpontjában a síkjára állított merőleges. Esesükben ezen rajta van az eredeti gömb középpontja is.
Tehát keressük a körülírt kör kp-ján és a gömb kp-ján átmenő egyenesnek és a gömbnek a megfelelő oldalon lévő metszéspontját.
(Ha nem elég, folytatom.)
|
| Előzmény: [1329] Tym0, 2010-01-04 20:40:33 |
|
| [1331] Tym0 | 2010-01-04 21:09:49 |
 kicsit érthetőbben? Mert ez nekem magas
|
|



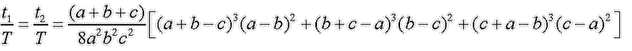



 , keleti hosszúság =
, keleti hosszúság = 
 legyen
legyen 

