| [1457] Lóczi Lajos | 2010-10-03 15:28:45 |
 Ahogyan már el is hangzott, ezek olyan elemi függvények, amelyeknek az inverze nem elemi függvény. Persze a függvény is és az inverze is hatványsorba fejthető például, amiből közelítő megoldásokat ki lehet olvasni.
|
| Előzmény: [1455] HoA, 2010-10-01 23:02:52 |
|
| [1456] jonas | 2010-10-02 17:18:57 |
 Az én kedvenc példám az efféle egyenletekre az, amikor egy ellipszispályán keringő bolygó helyét akarjuk megadni az idő függvényében. Ez általában egy sinx=ax+b típusú egyenletre vezet, aminek elemi függvényekkel nem lehet megtalálni a megoldását. A helyből az időt viszont vissza lehet számolni csak elemi függvényekkel.
|
|
| [1455] HoA | 2010-10-01 23:02:52 |
 Kedves matematikus fórum látogatók! Igen, azt hiszem itt az a kérdés, van-e valamilyen fogalom az ilyen értelemben nem invertálhazó függvényekre. Vagyis amikor y kifejezhető zárt alakban x függvényeként, például
y=x+sin(x)
, de x nem adható meg zárt alakban y függvényeként.
|
| Előzmény: [1454] Gubbubu, 2010-10-01 22:05:05 |
|
| [1454] Gubbubu | 2010-10-01 22:05:05 |
 Nem is az a fő baj, hogy transzcendens (tkp. az abszolútértékes egyenletek is transzcendensek, mégis szépen meg lehet őket oldani :-). Talán érdemes lenne a Wikipédiában megnézni az implicitfüggvény-tétel c. szócikket, az én ismerettáramban ez a legközelebbi fogalom, aminek egyáltalán köze lehet a feladatodhoz, bár hogy alkalmazható-e ... ? Amúgy a probléma maga szép, amit feladtál. :-)
|
| Előzmény: [1453] nadorp, 2010-10-01 12:15:55 |
|
| [1453] nadorp | 2010-10-01 12:15:55 |
 A végeredményed jó, de ebből r-t szerintem nem lehet kifejezni, mert ez egy transzcendens egyenlet. ( hasonlóan pld. az x=3sinx egyenlethez). Csak közelítő megoldás van.
|
| Előzmény: [1452] ojozso, 2010-09-29 20:20:00 |
|
| [1452] ojozso | 2010-09-29 20:20:00 |
 Köszi a választ!
Én is próbálkoztam a megoldással, mielőtt feltettem a Fórumra a feladatot, csak nem akartam befolyásolni vele senkit.
Most leírom, meddig jutottam el.
A körszelet területe (t): Tkorszelet=Tkorcikk-TQOCharomszog.
A HÁROMSZÖG TERÜLETE:
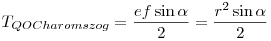 , mivel e=f=r , mivel e=f=r
OFQ derékszögű háromszögben (F az OC szakasz felezőpontja) OQF szög  fele. Szinusz definíciója alapján: fele. Szinusz definíciója alapján:
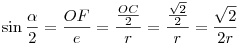 , mivel , mivel 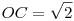 (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója). (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója).
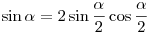 . (Kétszeres szög szinusza). A . (Kétszeres szög szinusza). A 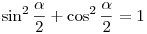 azonosságból: azonosságból: 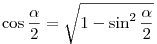 , melyet behelyettesítve kapjuk: , melyet behelyettesítve kapjuk:
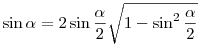 . Beírva . Beírva 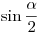 -re kapott -re kapott 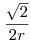 értéket: értéket:
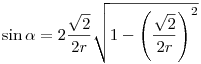 . Egyszerűbb alakra hozva megkapjuk, hogy . Egyszerűbb alakra hozva megkapjuk, hogy 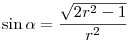
A háromszög területe tehát:
| (1) | 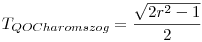 |
A KÖRCIKK TERÜLETE:
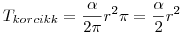 ( ( radiánban.), vagyis: radiánban.), vagyis:
| (2) | 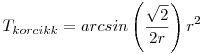 |
A KÖRSZELET TERÜLETE:
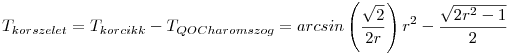
És itt a végállomás! Fogalmam sincs, hogyan lehetne ebből r-et kifejezni, már csak azért sem, mert r az arcsin argumentumában is szerepel és nem tudom, hogyan lehet onnan kihozni.
Innentől kéne segítség. Ráadásul abban sem vagyok biztos, hogy eredményem ekvivalens-e a Tieddel.
|
 |
| Előzmény: [1450] Gubbubu, 2010-09-28 12:19:53 |
|
|
| [1450] Gubbubu | 2010-09-28 12:19:53 |
 Az első feladatra nekem az 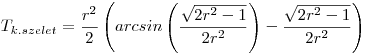
A megoldás leírásához szükséges időm most túl kevés, estefelé vagy pár nap múlva talán; így a képzeletbeli margón marad :-).
Szükséges lenne természetesen az ért. tartományok vizsgálata is, továbbá esetleges geometriai diszkusszió. Nagy vonalakban az történt, hogy kiszámolod a körcikk területét (ez egyszerű egyenes arányosság), majd az ún. trigonometrikus területképlettel az OAC háromszögét, és kivonod a kettőt egymásból. Ezután kifejezed az omega szöget az r segítségével (ehhez ügyeskedni kell az addíciós tételekkel), így eltüntetvén az omegát a képletből (opcionális, az arcsin-elt kifejezés egyébként maga a szinusz omega).
|
| Előzmény: [1449] ojozso, 2010-09-27 18:49:48 |
|
| [1449] ojozso | 2010-09-27 18:49:48 |
 Sziasztok!
Új vagyok itt és adódott egy probléma, melyen nem tudok túljutni, de Nektek bizonyára menni fog... Tehát:
172. feladat
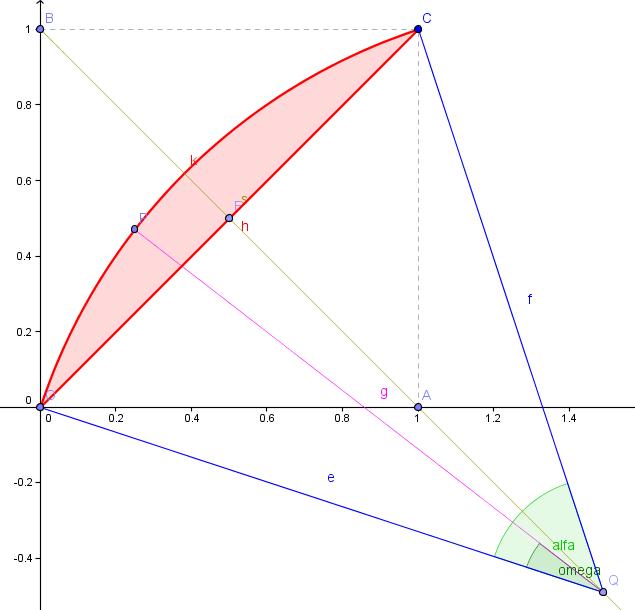
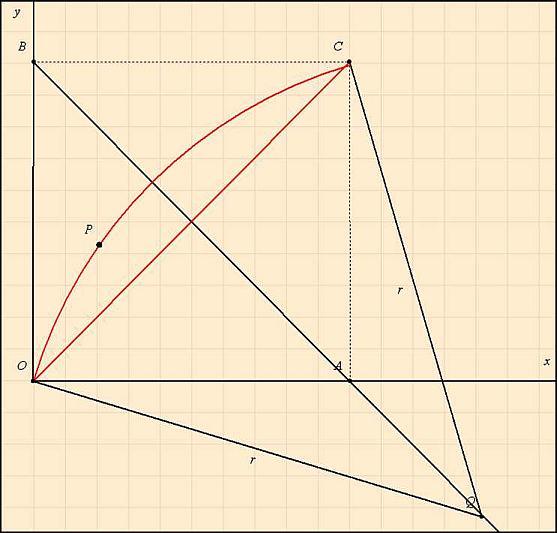
Jelöljük O-val az origót (0;0), A-val az (1;0), B-vel a (0;1) és C-vel az (1;1) pontokat. Az AB szakasz A ponton túli meghosszabításával kapott félegyenesen AB szakaszon kívül vegyünk fel egy tetszőleges Q (u;v) pontot. QO=QC=r sugárral rajzoljuk fel a Q középpontú OC körívet. Ezen a köríven vegyünk fel egy tetszőleges P (x;y) pontot. Az OC szakasz és az OC körív által (pirossal) határolt körszelet területét jelöljük t-vel, az OQP szöget pedig omega-val (QP szakasz sajnos, lemaradt a rajzról.)
Határozzuk meg az adott t területű körszelethez tartozó r sugarat!
Írjuk fel az adott adott t területű körszelethez tartozó körív tetszőleges P pontjának koordinátáit r és omega függvényében!
|
 |
|
|
| [1447] Csimby | 2010-09-08 02:16:06 |
 Szóval mindenképpen ajánljuk, hogy megrendeld a lapot és csináld a pontversenyt - szerintem rengeteget lehet tanulni belőle - de itt a fórumon többnyire más feladatok kerülnek elő!
|
| Előzmény: [1446] BohnerGéza, 2010-09-08 00:59:23 |
|
| [1446] BohnerGéza | 2010-09-08 00:59:23 |
 Természetesen sok a lapban megjelenő feladat is előkerül itt, de a kettő nem fedi egymást.
A Lapban sok érdekes feladat van különböző nehézségűek csoportosításával. Az "A" jelűek nehezek, könnyebbek a "B"-k, kezdőknek a "C" jelűek valók, illetve kifejezetten kilencedikeseknek szólnak a "K" jelűek. Számítástechnikai és fizikai rovat is található sok érdekes feladattal.
A feladatok mellett nívós cikkek is vannak, sok kitűzött feladat megoldása is szerepel, valamint a pontverseny állása is félidőben, illetve a végeredménye.
|
| Előzmény: [1443] kuklic, 2010-09-06 18:16:49 |
|
| [1443] kuklic | 2010-09-06 18:16:49 |
 A feladatokat amiket itt megoldtok, a megrendelt komal lapból csináljátok? mert ha igen akkor megrendelem én is :)
|
|
| [1442] BohnerGéza | 2010-09-04 11:44:38 |
 Néhány megjegyzés a 171. feladathoz, és HoA szép megoldásához:
- Ha érintőkörökkel definiálunk valamit, érdemes lehet analóg feladatokat is megfogalmazni! ... (Valaki a 171. feladathoz?)
- A trapéz átlóinak metszéspontján átmenő, az alapokkal párhuzamos egyenesnek a trapézban lévő szakasza az alapok harmonikus közepe. (Ezt a szakaszt felezi az átlók metszéspontja, tehát a feladatban a magasság felezőpontja szerepel.) Ebből is folytatható a "volt egyszer..." helyett HoA megoldása.
Érdemes lehet tudni:
Ha a trapéz szárait az alapok arányában osztjuk, az osztópontokat összekötő szakasz az alapok mértani közepe. (Ha fordított arányban osztjuk, azt nem tudom, érdemes lehet kiszámolni!)
A trapéz szárainak felezőpontjait összekötő szakasz az alapok számtani közepe.
Ha a trapézt az alapokkal párhuzamosan úgy osztjuk ketté, hogy a területét felezzük, az osztóvonal az alapok négyzetes közepe lesz.
Ezekkel két számra igazolhatóak a szereplő közepekre az egyenlőtlenségek.
|
| Előzmény: [1441] HoA, 2010-08-19 13:19:44 |
|
| [1441] HoA | 2010-08-19 13:19:44 |
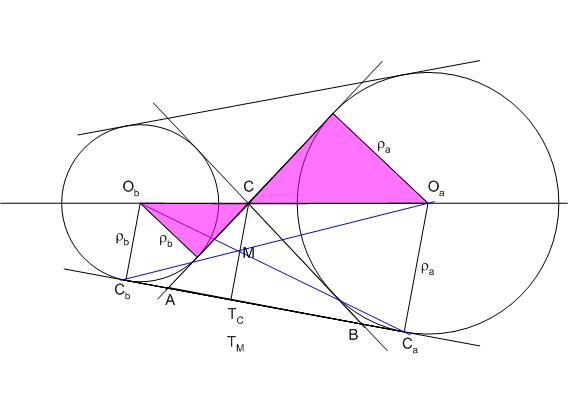
 Egészítsük ki az ábrát a hozzáírt körökkel és közös érintőikkel. A lila háromszögek hasonlóságából és a párhuzamos szelők tételéből 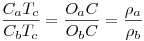 . Vagyis Tc a hozzáírt körök sugarainak arányában osztja a CaCb szakaszt. Az OaObCbCa derékszögű trapéz átlóinak M metszéspontjából CaCb -re bocsátott merőleges talppontja legyen TM Mivel CaTM és CbTM az OaCaM és ObCbM hasonló háromszögek megfelelő magasságai, ezek aránya is . Vagyis Tc a hozzáírt körök sugarainak arányában osztja a CaCb szakaszt. Az OaObCbCa derékszögű trapéz átlóinak M metszéspontjából CaCb -re bocsátott merőleges talppontja legyen TM Mivel CaTM és CbTM az OaCaM és ObCbM hasonló háromszögek megfelelő magasságai, ezek aránya is 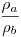 , TM és Tc egybeesik, M valóban rajta van CTc -n , TM és Tc egybeesik, M valóban rajta van CTc -n
Volt egyszer egy KöMaL feladat, amelyik azt kérdezte, megszerkeszthető-e a háromszög ha adott két hozzáírt kör sugara és a harmadik oldalhoz tartozó magasság. Eredményül persze kijött, hogy a három szakasz nem független, a magasság a két sugár harmonikus közepe, így vagy nincs megoldás vagy a feladat határozatlan. Ezt ismertnek feltételezve, a B 4276 annak bizonyítását kéri, hogy a harmonikus közép nem nagyobb a mértani középnél, ami e fórum látógatói számára érdektelen.
BohnerGéza ábrája viszont úgy is értelmezhető, hogyan szerkeszthetjük meg egyszerűen két szakasz harmonikus közepét. Hirtelenjében erre nem látok jobb megoldást.
|
 |
| Előzmény: [1440] BohnerGéza, 2010-08-04 02:02:39 |
|
| [1440] BohnerGéza | 2010-08-04 02:02:39 |
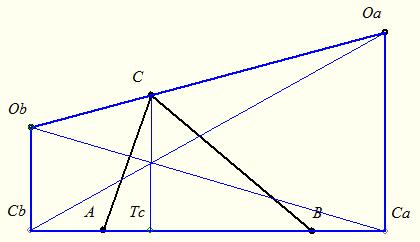
 171. feladat: A B.4276 feladattal kapcsolatban:
Az ABC háromszög két hozzáírt körének középpontja Oa és Ob, ezek érintési pontja az AB oldalon Ca és Cb A C-ből induló magasság CTc. Bizonyítandó, hogy OaCb és ObCa a CTc szakaszon metszik egymást.
|
 |
|
| [1439] gida1 | 2010-07-22 11:47:36 |
 Nagyon köszönöm, Jonas!
|
|
|
| [1437] gida1 | 2010-07-22 01:27:14 |
 Sziasztok! A segítségeteket kérném. Mi a magyar megfelelője az angol PERMUTOHEDRON-nak? Milyen éder? Segítségül egy link: http://en.wikipedia.org/wiki/Permutohedron
És mi az a BIPARITE GRAPH / BIGRAPH? http://en.wikipedia.org/wiki/Bipartite
Segítségeteket előre is köszönöm!
|
|
|
| [1435] S.Ákos | 2010-07-10 21:13:54 |
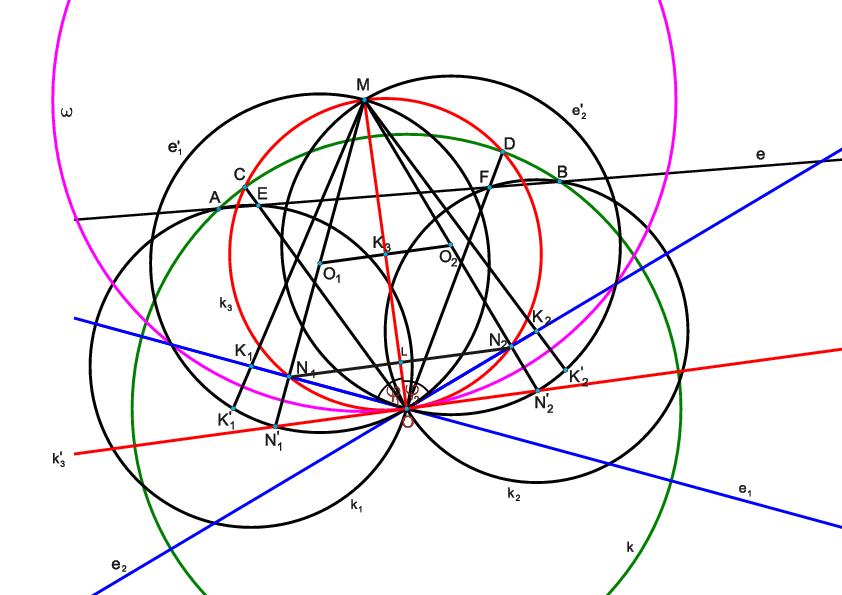
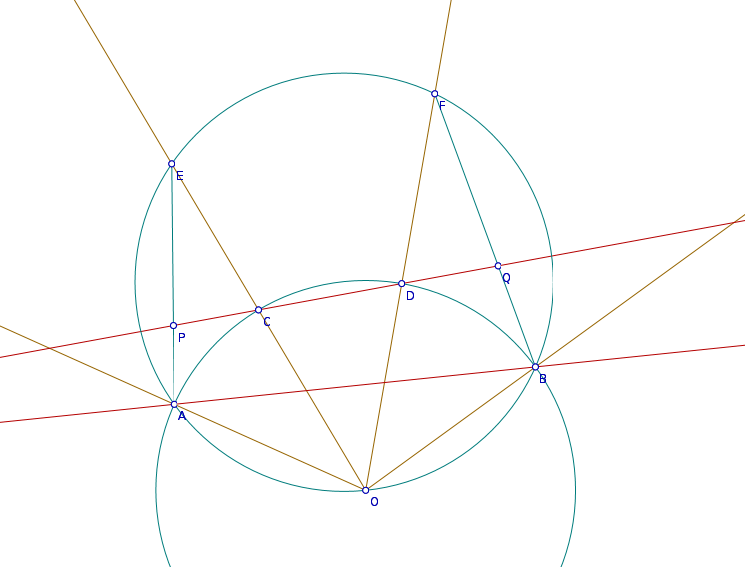
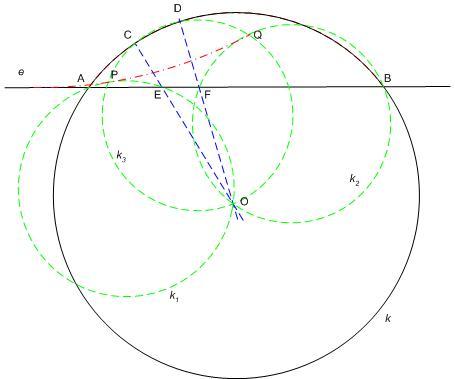
 170./a: k körre vonatkozó inverzióval, vázlatosan
AB képe az AOBFE kör, az O-n átmenő 3 kör (AEO, CDO, FBO képe 1-1 egyenes, rendre AE, CD, FB, AOB, AOC, COD, DOB egyenlőszárú háromszögek. Az állítás az, hogy EA és BF azonos szöget zár be CD-vel. Innét szögszámolással adódik, hogy tényleg egyenlő a két szög, (mondjuk legyen BAO =ABO =ABO = = és AOE és AOE = = 1, COD 1, COD = = 1, DOB 1, DOB = = 3). 3).
|
 |
| Előzmény: [1431] HoA, 2010-06-24 12:43:03 |
|
| [1434] sakkmath | 2010-07-10 20:46:09 |
 Túlbonyolítottam. Rájöttem, hogy nem kell az inverzió. Elég azt látni, hogy mivel a k3 körben N1 N2 húr, ezért őt merőlegesen felezi MO. Ezért az N1 N2 O háromszög egyenlő szárú, stb. (Elnézést.)
|
| Előzmény: [1433] sakkmath, 2010-07-10 18:59:21 |
|
|
|
| [1431] HoA | 2010-06-24 12:43:03 |
 170. feladat Az O középpontú k kört az e szelő az A és B pontokban metszi.Az AB ív C és D pontjába húzott sugár metszéspontja e-vel E és F.
a)Igazoljuk, hogy az AEO pontok k1 köre és a BFO pontok k2 köre azonos szögben metszi az OCD pontok k3 körét. Az O-tól különböző metszéspontok P és Q.
b)Bizonyítsuk be, hogy a k1-et P-ben és k2-t Q-ban érintő kör e-t is érinti.
|
 |
|







 fele. Szinusz definíciója alapján:
fele. Szinusz definíciója alapján: 








 =ABO
=ABO 1, COD
1, COD