| [1659] HoA | 2013-03-29 19:35:28 |
 Köszönöm. Természetesen én is be tudom bizonyítani. Csak arra nem emlékeztem - és ezért erre lennék kíváncsi - , milyen bizonyítás szerepel ma a tankönyvben. Vagy tudod, hogy ott is ez van?
|
| Előzmény: [1658] w, 2013-03-29 18:55:50 |
|
|
| [1657] HoA | 2013-03-29 15:07:43 |
 Előre is elnézést a kérdésért: Hogy bizonyítja manapság a középiskolai tankönyv, hogy ha egy konvex négyszög szemközti oldalainak összege egyenlő, akkor érintőnégyszög? ( A másik irányra emlékszem :-) )
|
| Előzmény: [1646] Fálesz Mihály, 2013-02-27 19:22:17 |
|
|
|
|
| [1653] Fálesz Mihály | 2013-03-12 20:43:45 |
 A gömbháromszög területét nem határozza meg egy oldal és a hozzá tartozó magasság.
Valójában a terület használatára nincs is szükség, az euklideszi háromszögekben az 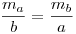 összefüggés egyszerű hasonlóságból jön ki. összefüggés egyszerű hasonlóságból jön ki.
|
| Előzmény: [1652] w, 2013-03-12 20:05:56 |
|
|
|
|
|
| [1648] nadorp | 2013-02-28 15:42:12 |
 A befogótétel csak derékszögű háromszögre alkalmazható, általános esetben sem. Inkább azon gondolkodj el, hogy minek a kiszámolásához használjuk leggyakrabban a háromszög magasságait?
|
| Előzmény: [1647] nyerek01, 2013-02-28 14:44:40 |
|
| [1647] nyerek01 | 2013-02-28 14:44:40 |
 Adott a lenti feladat: Egy háromszögben a=5,6 cm b=6,4 cm ma = 4 cm Mekkora mb? Befogotetellel probaltam megcsinalni, de elakadtam.
|
|
| [1646] Fálesz Mihály | 2013-02-27 19:22:17 |
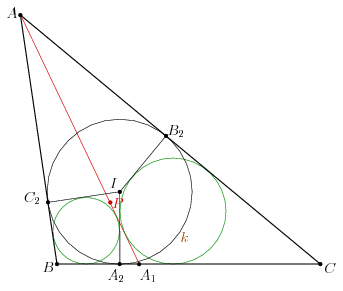
 A másik megoldást nem én találtam ki, a feladat kitűzőjétől származik.
Legyen I a beírt kör középpontja, az érintési pontok A2, B2 és C2. Az BA2IC2 és CB2IA2 deltoidokba írt körök egyik közös belső érintője az IA2 sugár. A másik közös érintő, csodák csodájára, átmegy az A csúcson...
|
 |
| Előzmény: [1645] Fálesz Mihály, 2013-02-27 19:10:32 |
|
| [1645] Fálesz Mihály | 2013-02-27 19:10:32 |
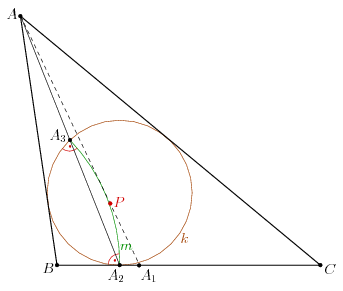
 Jó, mutatok két szerkesztést, de neked házi feladat kitalálni, hogy ezek miért működnek. Az elsőt én találtam ki.
Legyen k a beírt kör, A2 a k A-val szemközti érintési pontja, és legyen A3 az AA2 szakasz és k második metszéspontja. Legyen m az a körív a háromszög belsejében, ami A1-ban és A2-ben merőlegesen metszi k-t. Húzzunk A-ból érintőt m-hez; ez át fog menni a keresett P ponton, és kimetszi az A1 pontot a BC oldalon.
|
 |
| Előzmény: [1644] w, 2013-02-26 20:23:24 |
|
|
|
| [1642] w | 2013-02-23 17:33:59 |
 Na, ez már nem nehéz feladat, hanem szerintem elírás volt a Szőkefalvi-verseny kilencedikes fordulójában:
Adott ABC háromszög síkjában hat. meg azon P pontok halmazát, melyekre PA+BC=PB+AC=PC+AB.
|
|
| [1641] w | 2013-01-22 09:59:35 |
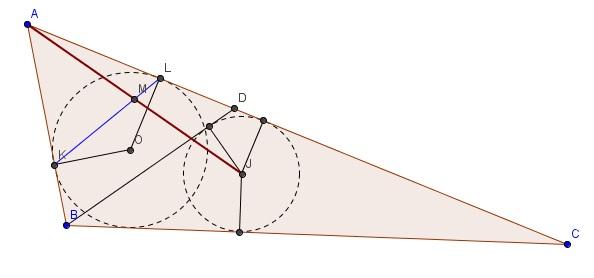
 Én is erre a megoldásra gondoltam (elvben). Talán még egyszerűbb lehetett volna, ha J-n keresztül párhuzamost húzol KL-lel, mert akkor a keletkezett szögek stb. tulajdonságait könnyebb megvizsgálni (meg természetes lépés, hogy igazolni akarjuk, hogy LM valamilyen módon középvonal). Nem feltétlenül kell akkor más, mint a 7. osztályos ismeretek, ami nem rossz egy olimpiai válogatóversenyről származó példától.
|
| Előzmény: [1640] HoA, 2013-01-22 00:31:15 |
|
|
|
| [1638] HoA | 2013-01-21 18:19:23 |
 Az mindenesetre látszik, hogy ha az arány a szögektől független állandó, akkor csak 1/1 ( felezés ) lehet, mert ha  növekszik és eléri a 90 fokot, akkor a két kör - és így O és J - egybeesik, AKOL = AKJL négyzet, melynek átlói felezik egymást :-) növekszik és eléri a 90 fokot, akkor a két kör - és így O és J - egybeesik, AKOL = AKJL négyzet, melynek átlói felezik egymást :-)
|
| Előzmény: [1637] w, 2013-01-20 16:02:33 |
|
|
|
|








 /2 ), OL és JN párhuzamosak, így PJ és LK ( LM ) is párhuzamosak , AJP és AML hasonló háromszögek, AP = AD + DP = 2 AT + 2 TL = 2 AL , AJ = 2 AM.
/2 ), OL és JN párhuzamosak, így PJ és LK ( LM ) is párhuzamosak , AJP és AML hasonló háromszögek, AP = AD + DP = 2 AT + 2 TL = 2 AL , AJ = 2 AM.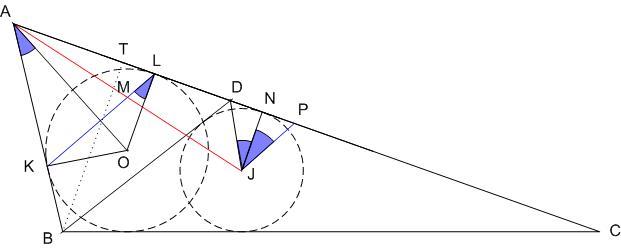
 <
<