|
|
| [1758] w | 2013-11-15 17:49:01 |
 Ez a megközelítés is nagyon tetszik, ezt nem vettem észre. (Amit írtam bizonyítás abból a tévhitből jött, hogy S1S2S3S4 az O1O2O3O4 négyszög beírt köre, aztán sikerült kipontosítani. :-)
|
| Előzmény: [1756] HoA, 2013-11-15 14:36:35 |
|
|
|
| [1754] Sinobi | 2013-11-13 18:13:22 |
 Ehhez kapcsolódik egy inverzós Monge-tétel bizonyítás.
Először belátjuk inverzióval a kis Monge-tételt három érintkező körről: k2 T1-ben és T3-ban érinti k1 és k3 köröket. Legyen Z a T1T3 egyenes és a k1 k3 centrálisának metszése. Innen egy olyan inverzió, amely kicseréli a T1 és T3 pontokat, helybenhagyja a k2 kört, mert kicseréli egy pontpárját. A k1 és k3 körök képeinek középponjtai a centrálison maradnak, és rajta maradnak az O2 T1 és az O2 T3 egyeneseken, tehát kicserélődnek. Három érintkező kör esetén T1 T3 átmegy k1 és k3 (egyik) egymásba invertálási pontján, és a k1-k3-at kicserélő inverzió helyben hagyja k2-t.
Három általános helyzetű körre pedig a bizonyítás: felveszek még két kört (k4-et és k5-öt), amely mind a három kört érinti, és akkor a k1-k2, k2-k3, k1-k3 körök (egyik) egymásba invertálási pontjai rajta fekszenek k4 és k5 hatványvonalán. Persze ez bizonyítás szinten sokkal-sokkal több szőrözést igényel, de legalább inverzió, körhatvány és efféle, és nem tér és projektív.
|
 |
| Előzmény: [1753] w, 2013-11-13 16:43:01 |
|
| [1753] w | 2013-11-13 16:43:01 |
 Egy lehetséges megoldás az A.597-re.
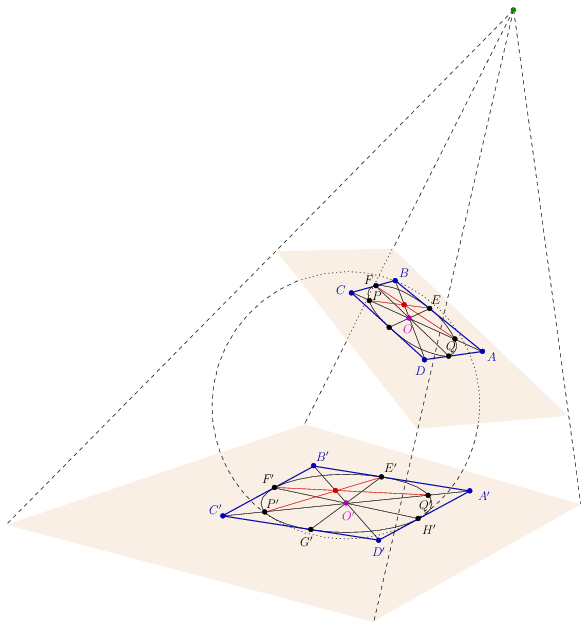
1. Felhasználjuk Monge tételét. Ez alapján kapjuk, hogy S1S2 S3S4 S3S4 T1T3=H13 és S2S3 T1T3=H13 és S2S3 S4S1 S4S1 T2T4=H24. T2T4=H24.
2. Rendkívül lényeges a következő lemma. Adott négy kör a síkon:  1, 1,  2, 2,  3, 3,  4, ahol 4, ahol  i és i és  i+1 az Ei pontban kívülről érinti egymást. Ekkor ha i+1 az Ei pontban kívülről érinti egymást. Ekkor ha  i középpontja Li, akkor L1L2L3L4 nyilván érintőnégyszög, de ekkor az LiLi+1Li+2 i középpontja Li, akkor L1L2L3L4 nyilván érintőnégyszög, de ekkor az LiLi+1Li+2 -ek szögfelezői egy pontban metszik egymást, ahonnan E1E2E3E4 húrnégyszög. -ek szögfelezői egy pontban metszik egymást, ahonnan E1E2E3E4 húrnégyszög.
3. Belátjuk, hogy az s:=S1S2S3S4 és a k0 körök hatványvonala H13H24. Valóban, például H13 hatványa k0-ra nézve H13T1.H13T3, s-re nézve pedig H13S1.H13S2. Ezek megegyeznek az előbbi lemma és a szelőtétel miatt. Hasonlóan, H24 is a hatványvonalon van, kész.
Legyen s középpontja 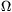 . Beláttuk, hogy O . Beláttuk, hogy O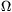 merőleges h:=H13H24 egyenesre. merőleges h:=H13H24 egyenesre.
4. Mivel azt már megmutattuk, hogy H13S3.H13S4=H13S1.H13S2=H13T1.H13T3, ezért k2, k4 és k0 körök hatványpontja H13. Hasonlóan, a k1, k3 és k0 körök hatványpontja H24. Vagyis H13 polárisa k0-ra nézve T2T4 és H24 polárisa T1T3. Innen OT is merőleges h-ra, tehát T O O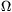 . .
5. A polaritás ismert tulajdonságai miatt H13H24 pólusa s-re nézve S. Következményül 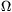 S is merőleges h-ra, azaz S S is merőleges h-ra, azaz S O O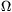 . .
Ezért O, T és S is rajta van O egyenesen. egyenesen.
|
|
|
|
| [1750] w | 2013-10-30 22:24:46 |
 Sejtés: a négy megadott pont (A,B,C,D) által meghatározott összes szakasz felezőpontjára illeszthető kúpszelet.
Azt először is érdemes meggondolni, hogy az imént megadott hat pont miért egy kúpszeleten van. Ehhez viszont elég észrevenni, hogy középvonalak miatt a hat pont által alkotott (egyik) hatszög szemközti oldalai párhuzamosak, így a Pascal-tétel megfordítása szerint egy kúpszeletre illeszkednek.
Igazából olyan O pontokra volna szükségünk, melyekre középpontosan tükrözve A,B,C,D pontokat, a kapott A',B',C',D' pontok a megadott pontokkal együtt egy kúpszeletre illeszkednek mind a nyolcan.
Nézzük meg először, hogy miért is van például AB szakasz felezőpontja a mértani helyen. Ekkor ugyanis A'=B és B'=A, emiatt igazából egy hatszögről lesz szó, és a középpontos tükrözés miatt a Pascal-tétel megfordítását használva kúpszeletre illeszkedik a hat pont (a hatszögüknek Pascal-egyenese ismét az ideális egyenes lesz). Ezzel megvan, hogy mind a hat felezőpont triviálisan a mértani hely része. Tehát elég belátnunk, hogy a keresett mértani hely kúpszelet.
De nézzünk meg tetszőleges O pontot is a síkon. O-ra tükrözve a megfelelő pontokat, figyeljük meg az ABCA'B'D hatszöget. Ez pontosan akkor lesz pascali, ha B'D BC és A'C BC és A'C AD pontok egy A'B'||AB-vel párhuzamos egyenest határoznak meg. Ily módon lehetne egy vektoros (?) bizonyítást adni a kúpszeletségre. AD pontok egy A'B'||AB-vel párhuzamos egyenest határoznak meg. Ily módon lehetne egy vektoros (?) bizonyítást adni a kúpszeletségre.
|
| Előzmény: [1749] Sinobi, 2013-10-30 20:58:07 |
|
| [1749] Sinobi | 2013-10-30 20:58:07 |
 Adott a síkon négy pont. Tekintsük az összes kúpszeletet, amelyek áthaladnak ezen a négy ponton. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
|
|
|
| [1747] Sinobi | 2013-10-25 11:48:47 |
 Egy M középpontú, k(M) paraméterű ("sugárnégyzetű") inverzió fixen hagyja a k kört (és a t kört is). Ahol k(M) az M pont k-ra vonatozó hatványa.
A szelőtétel értemében minden M-en átmenő szelőre igaz lesz, hogy az egyik metszéspont képe a másik, és a másik metszéspont képe az egyik lesz, tehát k fixen marad.
(ha M k-ra esik, akkor tényleg nem működik, máshogy kell meggondolni.)
|
| Előzmény: [1746] HoA, 2013-10-25 11:15:32 |
|
|
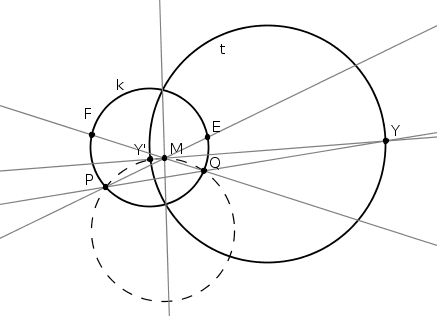
| [1745] Sinobi | 2013-10-12 22:45:10 |
 Az A.595-ös feladat is szépen megoldható majdnem kizárólag az inverzió fogalmait és tételeit használva. Megoldásvázlat:
1: Belátom, hogy AC, EF és GH egy pontban, Y-ban metszik egymást.
1.5: Y polárisa BD
2: tehát EP FQ BD-n helyezkedik el. FQ BD-n helyezkedik el.
1: bizonyítása: Legyen Y:=EF GH. Felveszem az A és C középponttú, AE és CF sugarú köröket. Y-ból egy olyan inverzió, amely k-t fixen hagyja kicseréli ezeket a köröket, tehát a középpontjukat összekötő AC egyenesen Y is rajta van. GH. Felveszem az A és C középponttú, AE és CF sugarú köröket. Y-ból egy olyan inverzió, amely k-t fixen hagyja kicseréli ezeket a köröket, tehát a középpontjukat összekötő AC egyenesen Y is rajta van.
1.5: ez nem inverzióval: Y rajta van B és D polárisán, tehát B és D rajta van Y polárisán.
2: azt fogom belátni, hogy ha Y-ból húzok két szelőt, amiknek a metszései k-val P,Q és E,F, akkor M:=EP FQ Y polárisán helyezkedik el.. FQ Y polárisán helyezkedik el..
Legyen az Y-ból húzott tetszőleges szelő két metszéspontja k körrel P és Q! Legyen M pont Y polárisának egy tetszőleges pontja! Vegyük fel YO (O k középpontja) Thalészkörét, legyen t. Egy olyan, Y kp-ú inverzió, amely k-t fixen hagyja, t-t Y polárisába viszi. Legyen Y':=YM t. Y' rajta van a PQM körön, mert az Y középponttú inverzió kicseréli M-t és Y'-t, és fixen hagyja a PQM kört. Az M kp-ú, k-t fixen hagyó inverzióra legyen P képe E, és Q képe F. Az inverzió fixen hagyja a t kört is, mert rajta van k és t hatványvonalán, és ha kicseréli k két pontját, akkor t-ét is. Ezért Y' képe Y, tehát PQM kör képe EFY egyenes. t. Y' rajta van a PQM körön, mert az Y középponttú inverzió kicseréli M-t és Y'-t, és fixen hagyja a PQM kört. Az M kp-ú, k-t fixen hagyó inverzióra legyen P képe E, és Q képe F. Az inverzió fixen hagyja a t kört is, mert rajta van k és t hatványvonalán, és ha kicseréli k két pontját, akkor t-ét is. Ezért Y' képe Y, tehát PQM kör képe EFY egyenes.
Ezzel beláttuk, hogy ha Y-ból húzunk egy szelőt (PQY), és felveszünk egy tetszőleges M pontot a polárisán, és vesszük az E:=PM k és F:=QM k és F:=QM k pontokat, akkor EFY egy egyenesbe esnek. k pontokat, akkor EFY egy egyenesbe esnek.
Ebből már következik PQY és EFY szelőkre, mert felvéve M pontot, mint PE és Y polárisának metszését, azt kapjuk, hogy F' egy olyan pont, amire F'EY egy egyenesbe esnek, és F' rajta van k-n, tehát F'=F, és M=EP FQ rajta van Y polárisán, BD-n. FQ rajta van Y polárisán, BD-n.
|
 |
|
| [1744] Sinobi | 2013-09-29 13:54:16 |
 Vagy elsiklottam felette, vagy nem igazoltad. Mindegy. Leölöm most őket, ne csúfoskodjanak itt a megoldásuk nélkül.
[1723]: Ha A és B rögzített, C egy AB-vel párhuzamos egyenesen futhat, mi ABC háromszög magasságpontjának mértani helye?
Tükrözöm az M pontot az AB egyenesre. A, B, C, M' egy körön van, és CM' merőleges AB-ra. Felveszem X pontot, mint CM' és AB metszéspontját. X körhatványa az ABCM' körre (x-a)(x-b), XC állandó, tehát M' egy (x-a)(x-b)/c egyenletű parabolát fog kirajzolni. Ennek tükörképe, M mértani helye is parabola. (ugyanígy ki kell hogy jöjjön ha a C pont egy AB-bal nem párhuzamos egyenesen fut, vagy egy AB-ot tartalmazó hiperbolán. AB-t tartalmazó parabolára is csak kis koordinátageometriázás. Geometriailag fogalmam nincs miért van így)
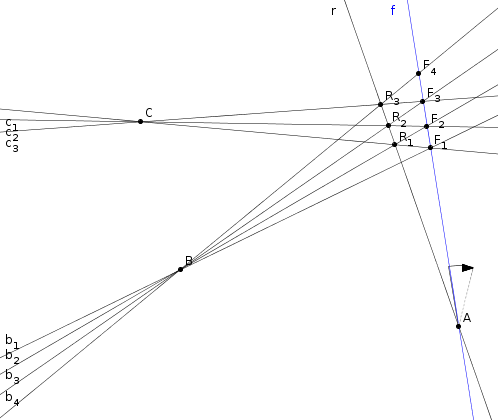
[1737]: Adott A, B, C pont a síkon. A-n átmegy egy rögzített r egyenes, és egy futó f egyenes, B-n egy rögzített b1 egyenes. Legyen Fi:=bi f, ci egyenes legyen Fi és C pontokon átmenő egyenes, Ri:=ci f, ci egyenes legyen Fi és C pontokon átmenő egyenes, Ri:=ci r és bi+1 legyen a B-n és a Ri pontokon átmenő egyenes. Mi a mértani helye Fi pontoknak? r és bi+1 legyen a B-n és a Ri pontokon átmenő egyenes. Mi a mértani helye Fi pontoknak?
A válasz: Fi egy i-edrendű görbén fog mozogni. Konkrétabban az x^i egy elprojektált képén. A "feladat" úgy született, hogy az a művelet, hogy veszek a koordinátarendszerben egy x-en futó X pontot, és a rá merőleges x=X egyenest, ennek az y=1-el való metszését, ennek az x=1 egyenesre vonatkozó vetületét, ennek az origóból az x=X-re vetítését, S.Í.T, és ez a művelet pont egy x-szel való szorzás, tehát a mértani helye az x^i görbe, ennek elprojektáltja a feladat.
[1740]: Adott P pont és c kör, c körön O és O' pontok. O és O' középponttú, P-n átmenő körök metszése legyen M. Hol van M, ha O' -> O. Mi M (határértékének) mértani helye, ha O befutja c-t? Igazold, hogy minden P-n átmenő, k-n levő középponttú kör érinti M mértani helyét!
M pont P pontnak a k kör O-ban levő érintőjére vett tükörképe. Ezt nem tudom belátni. M mértani helyét ha leinvertáljuk P-re, akkor egy hipikét kapunk, aminek minden P-n átmenő, k-n levő középponttú kör képe, amely egy egyenes, az érintője. Azaz geometriailag, analízis vagy ilyesmi okoskodás nélkül be lehet látni, hogy sok kör burkológörbéje (amit mindegyik érint) megegyezik azzal a görbével, amit úgy kapunk, hogy vesszük két egymáshoz nagyon közel levő kör metszspontjait, és ennek a mértanihelye. (ha van valakinél még ilyen típusú feladat (vagy tud konstruálni) akkor azt nekemadhatná)
[1741]: adott e, f, g és h egyenes és egy P pont, szerkessz olyan p egyenest P-n át, hogy 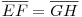 (ahol (ahol 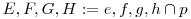 ) )
Ha EF=GH, akkor EH és GF felezőpontja ugyanott van. EH és GF felezőpontjának mértani helyei pedig hipikék, tehát két kúpszelet metszésével meg lehet szerkeszteni. (ez igaz minden kúpszeletre, hogy ha van egy kúpszeletem és egy pontom, akkor ha a pontból egyenesekkel metszem el a kúpszeletemet, és veszem a metszéspontok felezőpontjait, akkor azok mértani helye egy kúpszelet. Parabolára még nincs szép egyszerű bizonyításom.)
[1741]: adott e és f egyenes, P pont. Szerkessz olyan p egyenest P-n át, hogy 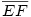 minimális legyen. ( minimális legyen. (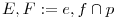 ) )
e és f metszéspontja legyen O. OP Thalész-körének és a P-n átmenő, e és f aszimptotájú hiperbolának a metszése legyen Q. PQ az az egyenes, amely átmegy P-n, és az e és f közé eső szakasza a legrövidebb. Ezt is itt hagyom belátni, vagy megcáfolni.
Másodrendű görbés szerkesztésekből is kéne nekem még több, hogy okosabb legyek másodrendű görbés szerkesztésekből.
|
| Előzmény: [1725] w, 2013-06-05 22:02:48 |
|
| [1743] Vonka Vilmos Úr | 2013-09-06 11:17:16 |
 Ez a megoldás talán inkább a projektív geometria témába illene, de sebaj.
Lemma. Legyen P az AB és A1B1 egyenesek közös pontja! Ekkor PF érinti k-t.
Bizonyítás. Legyen Y az XF érintő és BC közös pontja. Jelölje F' a k-hoz P-ből húzott AB-től különböző érintő és az XY egyenes metszéspontját. Azt kell megmutatnunk, hogy F' XY felezőpontja, azaz F'=F. Alkalmazzuk a Brianchon-tételt az 123456 hatszögre, ahol 1=2 az AC egyenes, 3=BC, 4=AB, 5=PF', 6=XY. Azt kapjuk, hogy A1B1, CF' és BX egy ponton megy át. Ismét alkalmazzuk a Brianchon-tételt, az AC és BC oldalak szerepének felcserélésével. Ekkor azt kapjuk, hogy A1B1, CF' és AY egy ponton megy át. A két eredményből együtt adódik, hogy az ABXY teljes négyszög AY BX átlóspontja illeszkedik CF'-re. Tehát F' XY-ra vonatkozó harmonikus társa a négyszög harmadik átlóspontja, ami az AB és XY egyenesek közös ideális pontja. Az ideális pont harmonikus társa azonban ismert módon a felezőpont. BX átlóspontja illeszkedik CF'-re. Tehát F' XY-ra vonatkozó harmonikus társa a négyszög harmadik átlóspontja, ami az AB és XY egyenesek közös ideális pontja. Az ideális pont harmonikus társa azonban ismert módon a felezőpont.
A lemma igazolása után rátérünk az állítás bizonyítására. Ehhez ismét a Brianchon-tételt alkalmazzuk a következő 123456 hatszögre: 1=6=AC, 2=3=AB, 4=PF, 5=XY. Ekkor 12 és 45 összekötő egyenese AF, 23 és 56 összekötő egyenese C1X, 34 és 61 összekötő egyenese PB1=A1B1. Így a Brianchon-tétel éppen a kívánt állítást adja.
|
| Előzmény: [1742] w, 2013-09-04 16:40:08 |
|
| [1742] w | 2013-09-04 16:40:08 |
 N+1-edik feladat. Legyen ABC tetszőleges háromszög, és k a beírt köre, ami a megfelelő oldalakat A1, B1, C1 pontokban érinti. Az AB-vel párhuzamos k-t érintő egyenes AC és BC közé eső szakaszának felezőpontja F, és az F-ből k-hoz AB-vel párhuzamosan húzott érintő AC-t X-ben metszi. Mutassuk meg, hogy XC1, A1B1 és AF egy ponton haladnak át.
|
|
| [1741] Sinobi | 2013-07-30 01:26:24 |
 március8 a szögharmadolás topicban:
,,Például egy ilyen: Adott a síkon két egymásra merőleges egyenes, és adott egy pont, amelyik az egyik adott egyenestől "p" távol van, a másik adott egyenestől "q" távol van. Szerkesztendő olyan egyenes, amely átmegy az adott ponton és amelynek a két adott egyenes közötti részének hossza "d". "
Ez érdekelne, de nem jöttem rá. Viszont például triviálisan megszerkeszthető kagylógörbe felvételével. De én polinomok gyökének megszerkesztése helyett (a polinomok csak koordinátázva kaphatók meg) inkább a görbézős szerkesztések felé mennék tovább.
Van két hasonló példám, amik kúpszeletelővel megoldhatók (egy kúpszeletelő kúpszeletet helyez néhány ponton és érintőn át, beleértve a végtelen távoli pontokat és egyenest is, és két ily módon kapott kúpszelet metszései szerkesztett pontnak számítanak)
első, ez egyszerűbb: adott e, f, g és h egyenes és egy P pont, szerkessz olyan p egyenest P-n át, hogy 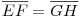 (ahol (ahol 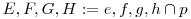 ) )
második: adott e és f egyenes, P pont. Szerkessz olyan p egyenest P-n át, hogy  minimális legyen. ( minimális legyen. ( ) )
(nem biztos, hogy kúpszeletelők segítsége nélkül nem lehet őket megoldani)
|
|
| [1740] Sinobi | 2013-07-12 01:42:54 |
 Adott P pont és c kör, c körön O és O' pontok. O és O' középponttú, P-n átmenő körök metszése legyen M. Hol van M, ha O' -> O. Mi M (határértékének) mértani helye, ha O befutja c-t? Igazold, hogy minden P-n átmenő, k-n levő középponttú kör érinti M mértani helyét!
------
Adott e, f és g egyenes, g-n P és P' pontok. P pont merőleges vetülete e-re és f-re Pe és Pf, Pe-n és Pf-n átmenő egyenes legyen p. p' egyenes hasonlóan. Adott P esetén hol metszi p-t p', ha P' -> P?
-------
Adott O origó, z origó körüli forgatva nyújtás, e egyenes, rajta E és E'. zE:=z(E), és f legyen az E és zE pontokon átmenő egyenes, f' hasonlóan. Szerkeszd (találd) meg f és f' F metszésének helyét, ha E adott, és E' -> E. Mi F mértani helye, ha E végigfut e-n? Igazold, hogy minden E-re f érinti F mértani helyét!
(geogebrában a rögzített, kicsi sugarú körrel lehet az alakzatból kimetszeni olyan pontot, amely mindig rajta van az alakzaton, és mindig nagyon közel marad a kör középpontja futóponthoz)
|
|
|
| [1738] w | 2013-07-08 00:27:57 |
 Vonka Vilmos szép okfejtéséből kiindulva megkérdezhetjük, hogy mikor igaz, hogy a három átlót azonos arányban osztó pontok mikor vannak egy egyenesen.
|
| Előzmény: [1735] Sinobi, 2013-07-07 19:32:54 |
|
|
| [1736] Vonka Vilmos Úr | 2013-07-07 20:47:06 |
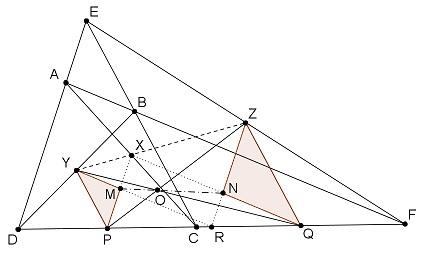
 Legyen az AC átló felezőpontja X, a BD átló felezőpontja Y, EF felezőpontja Z. Legyen továbbá P CD felezőpontja, Q CF felezőpontja és R DF felezőpontja. YP BCD középvonala, ZQ ECF középvonala, ezért YZ és ZQ egyaránt párhuzamos CE-vel. Tehát YP és ZQ párhuzamos. Hasonlóan: XP és ZR párhuzamos, valamint YC és QX is párhuzamos. Így az ábrán szereplő YMP és QNZ háromszögek megfelelő oldalegyenesei párhuzamosak, vagyis a két háromszög középpontosan hasonló. Tehát YQ, MN és PZ egy O pontra illeszkednek. Ekkor a Papposz-tételt a kollineáris PRQ és és MON ponthármasokra alkalmazva adódik az állítás.
|
 |
| Előzmény: [1735] Sinobi, 2013-07-07 19:32:54 |
|
| [1735] Sinobi | 2013-07-07 19:32:54 |
 Igazoljuk, hogy egy négyszög három átlójának felezőpontja (ahol a harmadik átló az átlóspontokat összekötő szakasz) kollineáris.
|
|



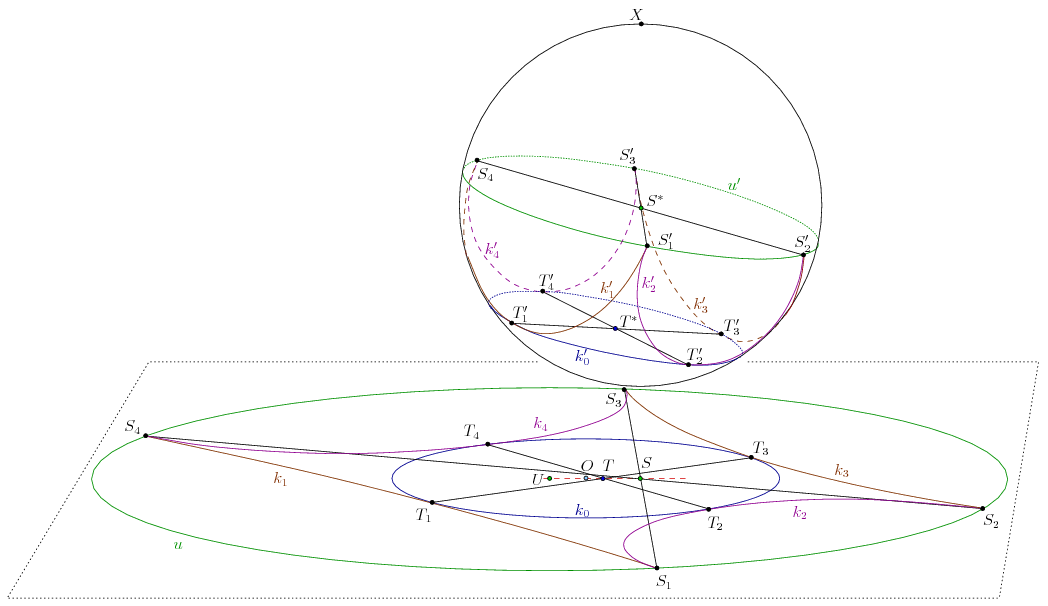


 =LiSi+1Si
=LiSi+1Si .
.
 >1 , S1S2 másik metszéspontja k3 -mal P , S3S4 -é Q . A hasonlóság miatt H13S4=
>1 , S1S2 másik metszéspontja k3 -mal P , S3S4 -é Q . A hasonlóság miatt H13S4=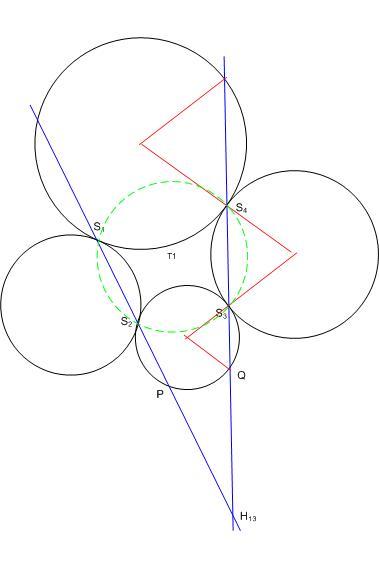


 S3S4
S3S4 1,
1,  . Beláttuk, hogy O
. Beláttuk, hogy O O
O