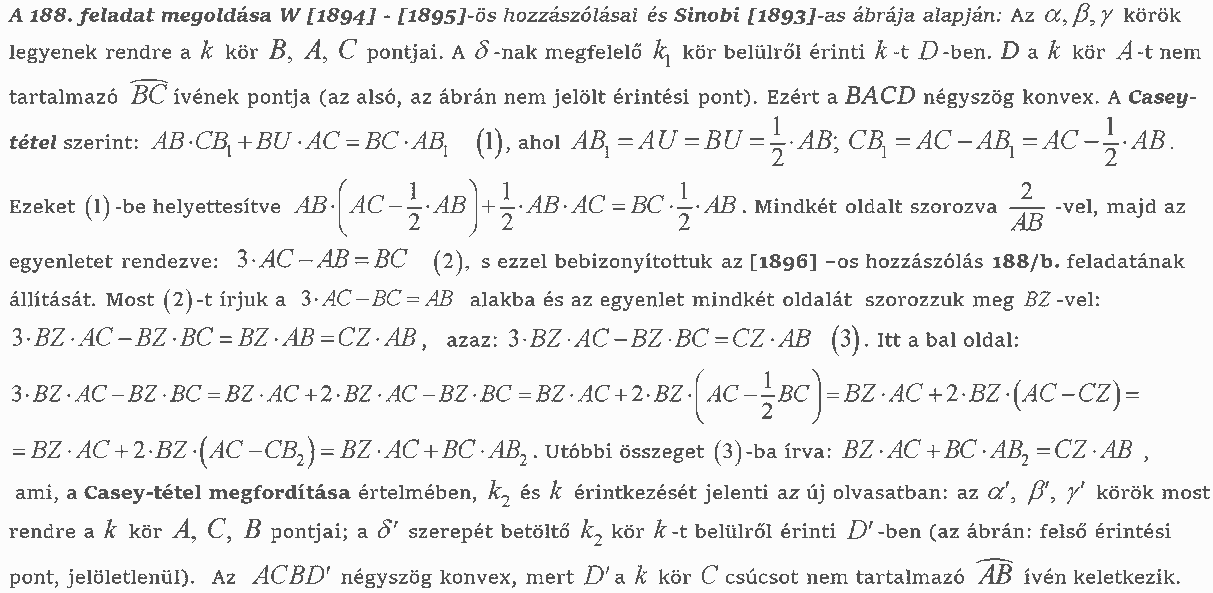| [1910] Gergely99 | 2016-11-23 23:03:35 |
 Ez egy lehetséges megoldás lenne, de a feladat nem írta sehol, hogy a háromszög derékszögű. Ezért nem tudtam boldogulni a feladattal. Szóval a kérdés ugyan az, csak annyival kiegészítve, hogy mi van, ha a háromszögem tetszőleges?
|
|
| [1909] jonas | 2016-11-23 14:36:41 |
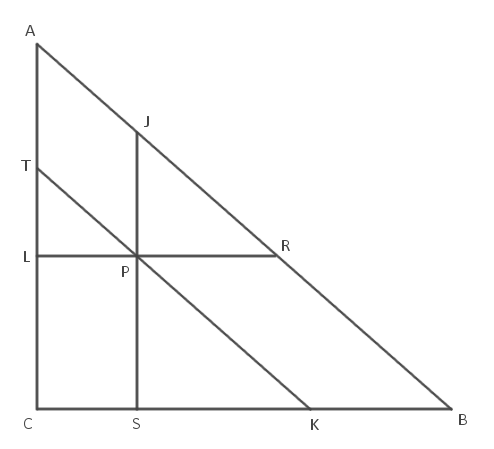
 Legyen a háromszög ABC, a belül felvett pont P. A P ponton át az AB oldallal párhuzamos a BC oldalt K-ban, az CA oldalt T-ben metszi; a BC oldallal párhuzamos az CA oldalt L-ben, az AB oldalt R-ben metszi; végül a CA oldallal párhuzamos az AB oldalt J-ben, a BC oldalt S-ben metszi.
A három kis háromszög, amiről a feladat beszél, PLT, RPJ, KSP. Vedd észre, hogy ez a három háromszög hasonló, mivel minden oldaluk párhuzamos egymással. Ráadásul a BCA háromszög is hasonló az előbbi háromhoz.
Legyen a PLT háromszög területe 1, az RPJ háromszög területe 2, a KSP háromszög területe 3. (Feltehetjük, hogy pont ilyen sorrendben vannak a területek, mert az eredeti háromszög ABC csúcsait betűzhetjük megfelelően.) Mivel az RPJ háromszög hasonló a PLT-hez, de kétszer akkora területű, ezért az oldalai \(\displaystyle \sqrt 2 \)-szer akkorák. Hasonlóan a KSP háromszög oldalai \(\displaystyle \sqrt 3 \)-szor akkorák, mint a PLT-é.
Mivel párhuzamosokat húztunk, a PJAT négyszög paralelogramma, így a TA szakasz hossza megegyezik a PJ szakasz hosszával, ez utóbbiról pedig a PLT és RPJ háromszögekből tudjuk, hogy \(\displaystyle \sqrt 2 \)-szer akkora, mint az LT szakasz. Hasonlóan PSCL is paralellogramma, így az LC ugyanolyan hosszú mint a PS szakasz, ez pedig \(\displaystyle \sqrt 3 \)-szor olyan hosszú, mint az LT szakasz.
Mármost mivel P a háromszög belső pontja, és PL párhuzamos BC-vel, ezért L a BC szakasz belső pontja. Hasonlóan PT párhuzamos AB-vel, ez pedig egy egyenesbe esik AR-rel, P pedig R és L között van, ezért T az AL szakasz belsejében van.
Ezekből az LA szakaszt a T belső pont az TA és a LT szakszra bontja, amik közül az AT-ről már megállapítottuk, hogy \(\displaystyle \sqrt 2 \)-szer olyan hosszú, mint LT, így az LA szakasz \(\displaystyle \sqrt 2 + 1 \)-szer olyan hosszú, mint LT. Hasonlóan a CA szakaszt L felbontja az LA és LC szakaszra, ezért a CA szakasz \(\displaystyle \sqrt 2 + 1 + \sqrt 3 \)-szor olyan hosszú, mint LT. Viszont a BCA háromszög hasonló a PLT háromszöghöz, és az utóbbinak a területe 1, ezért az oldalak arányából az előbbinek a területe \(\displaystyle (\sqrt2 + 1 + \sqrt3)^2 \), ami körülbelül 19.17.
|
 |
| Előzmény: [1908] Gergely99, 2016-11-22 21:10:01 |
|
| [1908] Gergely99 | 2016-11-22 21:10:01 |
 Jó estét kívánok mindenkinek!
Volna egy olyan feladatom, aminek nem tudom, hogy hogyan álljak neki, de szeretném nagyon megoldani. Pusztán kíváncsiságból szeretném megtudni, hogy hogyan kellene a feladatot megoldani.
Ez lenne a feladat:
Egy háromszög belsejében felvett ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszöget 6 részre osztják. Mekkora az eredeti háromszög területe, ha a keletkezett 3 háromszög területe: 1, 2 illetve 3 egység?
|
|
| [1907] Dömötör Erzsi | 2016-10-28 23:19:25 |
 Talán nem tartjátok OFF-nak a témát, ha nem a geometria szépségeiről írok, hanem arról, aki e fórum keretein belül olyan sok gondolatát megosztotta velünk :(
|
 |
|
| [1906] jonas | 2016-10-14 15:16:25 |
 Forgassuk el az \(\displaystyle SQ \) szakaszt derékszöggel, és toljuk el, hogy az egyik végpontja \(\displaystyle P \)-be kerüljön, így kapjuk a \(\displaystyle PT \) szakaszt. A kulcs észrevétel, hogy az \(\displaystyle RT \) egyenes megegyezik a négyzet \(\displaystyle CD \) oldalegyenesével. A másik három oldalegyenest úgy kapjuk, hogy \(\displaystyle P \)-n át párhuzamost húzunk \(\displaystyle RT \)-vel, majd \(\displaystyle Q \)-n és \(\displaystyle S \)-en át merőlegest \(\displaystyle RT \)-vel.
Csakhogy ebben a szerkesztésben a \(\displaystyle T \) pontra két lehetőséget kapunk a szerint, hogy az elforgatott szakasz melyik végpontja kerül \(\displaystyle P \)-be. A két lehetőség két ellentétes körüljárású négyzetet ad.
Speciális esetek. Ha \(\displaystyle R = T \), de \(\displaystyle P \ne T \), akkor van végtelen sok különböző négyzet, mégpedig bármilyen irányú oldalegyeneshez egy, kivéve a \(\displaystyle PR \)-rel párhuzamos vagy merőleges irányt. Ha \(\displaystyle PTR \) kollineáris, de \(\displaystyle R \ne T \), akkor nincs megoldás.
Ha a feladatkiírást úgy értelmezed, hogy \(\displaystyle P \) az \(\displaystyle AB \) szakaszon legyen stb, akkor minden megoldást ellenőrizni kell, hogy az adott pontok tényleg a szakaszokon vannak, nem az oldalegyenesek valamely másik részén. Ekkor a tipikus esetben legfeljebb egy megoldás lehet.
|
| Előzmény: [1905] w, 2016-10-13 18:46:54 |
|
| [1905] w | 2016-10-13 18:46:54 |
 Adottak a síkon a \(\displaystyle P,Q,R,S\) pontok. Szerkesszünk olyan \(\displaystyle ABCD\) négyzetet, melyre \(\displaystyle P\in AB\), \(\displaystyle Q\in BC\), \(\displaystyle R\in CD\), \(\displaystyle S\in DA\)!
|
|
| [1904] Sinobi | 2016-07-27 00:31:12 |
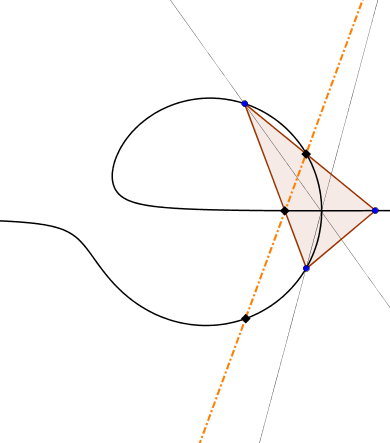
 189. feladat: Legyen &tex;\displaystyle \vartheta&xet; két, közös végpontú szakasz, HI és IJ ekvioptikus görbéje (azaz: azon P pontok mértani helye, melyekre HPJ egyik szögfelezője átmegy I-n)
Bizonyítsuk be, hogy ha A,B,C &tex;\displaystyle \in \vartheta&xet; háromszög a görbén fekszik úgy, hogy ABC beírt körének középpontja I, akkor EFG egy egyenesre illeszkednek, amennyiben &tex;\displaystyle \{E,F,G\} = ABC \cap \vartheta&xet; A,B,C-tól különböző metszéspontjai.
|
 |
|
| [1903] Sinobi | 2016-05-30 13:42:45 |
 > Adott a síkon négy egyenes. Tekintsük az összes kúpszeletet, amelyek érintik ezt a négy egyenest. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
Ezt is én, nem lett megoldva (számozni kéne??). A válasz az hogy a Newton érintőnégyszög tétele értelmében az átlók felezőpontjait összekötő egyenesen lesz. (Ellipszisre úgy megy, hogy körré affinítod, és alkalmazod Newton tételét. Hiperbolára mondjuk úgy, hogy veszed ugyanazt a bizonyítást a Minkowski síkon, és megkapod derékszögű hiperbolára a tételt. Másik lehetőség, hogy tükrözöl a kúpszelet középpontjára, és akkor a Brianchon azonnal adja.) (.. minden testre működik ez a bizonyítás, nem? Létezik 4 egyeneshez mindig érintő kúpszelet, kúpszeletnek középpont, középpontnak tükrözés, illetve Brianchon..?)
.. mi a helyzet magasabb dimenzióban? Két adott másodrendű felület lineáris kombinációnak a középpontjainak mi a mértani helye? N síkot érintő másodrendű felületek középpontjainak?
(Én nem tudom.)
.. van valakinek szakirodalma másodrendű felületsorokról?
|
| Előzmény: [1776] Sinobi, 2013-12-11 18:15:18 |
|
| [1902] Sinobi | 2016-05-26 03:49:47 |
 >> Kúpszeletsor középpontjának mértani helye?
> Sejtés: a négy megadott pont (A,B,C,D) által meghatározott összes szakasz felezőpontjára illeszthető kúpszelet.
Egy geometriai megoldás:
Ha a négy pont konkáv, akkor egy ortogonális négyesbe affinítod őket. Ekkor az összes rajtuk átmenő kúpszelet merőleges parabola lesz, és a középpontjuk a négyszög Feuerbach-körén lesz. Ezt nem nehéz belátni.
Ha a négy pontod konvex, akkor húrnégyszöggé affinítod, és, még sokkal egyszerűbben be lehet látni hogy az ilyen középpontok mértani helye egy merőleges hipike. (Nagyon érdemes észben tartani, hogy merőleges hipikét kapsz akkor ha egy sugársort csúsztatva tükrözöl és elmetszel önmagával, és általában csak ilyenkor.)
(Ha a négy pont trapéz akkor közelíted nem trapézokkal, a mértani hely is folytonosan fog változni.)
Ez egy nagyon erős és jól használható módszer, érdemes észbentartani. (Nem is gondolná az ember, hogy mi minden affin/vektoros, ami elsőre nem tűnik annak.)
|
| Előzmény: [1750] w, 2013-10-30 22:24:46 |
|
|
| [1900] sakkmath | 2016-03-14 20:46:35 |
 A 188. feladat a 185. köpönyegéből bújt elő, ezért HoA [1899]-es szép megoldása - átbetűzések után - megoldja 188-at is.
Utóbbira felteszek egy új megoldást, amely a Casey-tételkört érinti oda-vissza. Egyúttal köszönöm W-nek, hogy a témáról alapos összegzést adott [1894]-[1895]-ben.
|
 |
|
| [1899] HoA | 2016-02-15 11:00:17 |
 Ha már ismét előjött Sawayama, felteszem elemi megoldásomat a 185. feladatra ( KöMaL 1285. feladat, ld itt [1879]) mielőtt feledésbe merül.
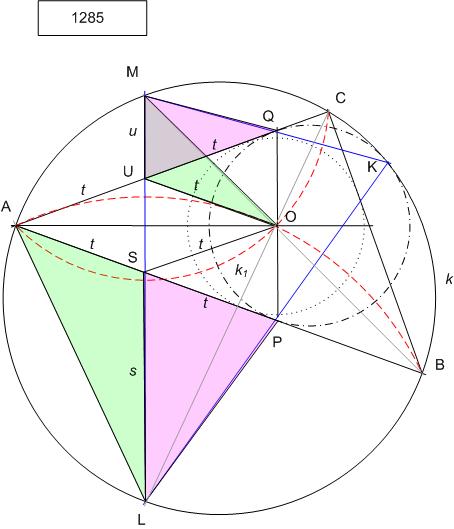
Legyen a körülírt kör &tex;\displaystyle k&xet;, az AB-t P-ben , AC-t Q-ban érintő kör &tex;\displaystyle k_1&xet; , külső hasonlósági pontjuk K, erről fogjuk megmutatni, hogy rajta van &tex;\displaystyle k&xet;-n. Itt is igaz, mint [1880] –ban, hogy a hasonlóságban P ill Q megfelelői az AB, AC ívek L ill. M felezőpontjai. Ismert, hogy az M középpontú MA sugarú és az L középpontú LA sugarú körök O-n is átmennek, ezért AO e két kör közös húrja, centrálisuk, LM ennek felező merőlegese. A BO és CO szögfelezők &tex;\displaystyle k&xet;-t M-ben ill. L-ben metszik. LM metszéspontja AB-vel ill. AC-vel legyen S ill. U. AO szögfelező, így ASOU rombusz, oldalhossza legyen t. A párhuzamos szelők tétele miatt t hosszúságú SP és UQ is. LSA és OUM &tex;\displaystyle \Delta&xet; -ek hasonlók, mert S-nél ill. U-nál lévő szögeik váltószögek, A-nál ill. M-nél lévő szögeik pedig az LB ívhez tartozó kerületi szögek. Innen az oldalak arányára
&tex;\displaystyle t / s = u/t &xet;
Emiatt hasonlóak a &tex;\displaystyle h_1&xet; = PSL és &tex;\displaystyle h_2&xet; = MUQ &tex;\displaystyle \Delta&xet;-ek, mert megegyeznek két oldal arányában és a közbezárt szögben ( S –nél ill. U-nál fekvő szögük az ASOU rombusz ASU = AUS félszögének csúcsszögei ) . &tex;\displaystyle h_1&xet;-hez és &tex;\displaystyle h_2&xet;-höz hasonló a &tex;\displaystyle h_3&xet; = KML &tex;\displaystyle \Delta&xet; , mert két szöge ( M-nél ill. L-nél ) megegyezik az előbbiek egy-egy, egymásnak nem megfelelő szögével. LKM &tex;\displaystyle \angle&xet; = MUQ &tex;\displaystyle \angle&xet;= AUS &tex;\displaystyle \angle&xet; = 90 – &tex;\displaystyle \alpha&xet;/2 , ami megegyezik az ML = MA + AL ívhez tartozó &tex;\displaystyle \beta&xet;/2 + &tex;\displaystyle \gamma&xet;/2 kerületi szöggel, K tehát rajta van k-n.
|
 |
| Előzmény: [1893] Sinobi, 2016-01-23 21:43:39 |
|
| [1898] Sinobi | 2016-01-31 20:53:15 |
 amúgy ez a koaxális körös, ez koaxiális akar lenni, vagy, valahonnan máshonnan kapta a nevét? Úgy sem látom több értelmét, de legalább valamit jelent. (valami olyat, amit én is ismerek)
|
| Előzmény: [1894] w, 2016-01-24 00:14:41 |
|
| [1897] Sinobi | 2016-01-31 19:19:19 |
 Hát, a Ptoleimaiosz-ból (és a koaxális körök lemmájából) azonnal adódik:
Ha az alsó érintési pont D, D-ből a megfelelő távolságok &tex;\displaystyle a,b,c&xet; (ahol &tex;\displaystyle a=b&xet;); és l az az arány, hogy l*i az i. pont &tex;\displaystyle k_1&xet;-hez húzott érintőjének a hossza, akkor:
&tex;\displaystyle \frac{AB+BC}{AC}=\frac{l(a+b)+BC}{l(a+c)}&xet;
ahol a Ptolemaiosz-tétel értelmében
&tex;\displaystyle BC \cdot a = c \cdot l (a+b) ~ + ~ b \cdot l (a+c)=3 l a c + l a^2&xet;
azaz &tex;\displaystyle BC=3 l c + l a&xet;, és &tex;\displaystyle \frac{AB+BC}{AC}=3&xet;.
(Valószínűleg kis módosítással adódik, hogy ha U nem az AB felezőpontja, és, D nem az AB felező merőlegesén van (hanem az egyik Apollóniusz-körén), akkor, ez az arány így is konstans. Bár az előbb 'véletlen' volt, hogy kiestek a dolgok.)
.. valaki ismer erre szépet? Nézegettem az előbb belinkelt Poncelet-eset, ott hasonló konfigurációk vannak, de, ahogy néztem pont ez nincs. .. mert az összefüggés nagyon szép rövid, egyszerű.
|
| Előzmény: [1896] spongya, 2016-01-31 16:43:50 |
|
| [1896] spongya | 2016-01-31 16:43:50 |
 Ez rövid volt, gratula!
Geom.progival nézegetve, az oldalak hosszaira ez állhat:
&tex;\displaystyle {AB + BC = {\it 3}\cdot AC}.&xet;
Bizonyítsuk be a fenti összefüggést! (188/b. feladat)
|
| Előzmény: [1893] Sinobi, 2016-01-23 21:43:39 |
|
| [1895] w | 2016-01-24 00:16:12 |
 Casey-tétel. Adott a &tex;\displaystyle k&xet; irányított kör és az azt &tex;\displaystyle A,B,C,D&xet; pontokban érintő &tex;\displaystyle \alpha,\beta,\gamma,\delta&xet; irányított körök. Ekkor ha &tex;\displaystyle ABCD&xet; négyszög konvex, akkor
| &tex;\displaystyle t_{\alpha\beta}t_{\gamma\delta}+ t_{\alpha\delta}t_{\beta\gamma}=t_{\alpha\gamma}t_{\beta\delta}.&xet; | (*) |
Casey-tétel megfordítása. Adott négy irányított kör a síkon: &tex;\displaystyle \alpha,\beta,\gamma,\delta&xet;. Ekkor ha teljesítik a &tex;\displaystyle (*)&xet; összefüggést, akkor van olyan irányított &tex;\displaystyle k&xet; kör vagy olyan egyenes, amely mind a négyet érinti.
&tex;\displaystyle &xet;
Bizonyítás. Maga a Casey-tétel egyszerű következménye a &tex;\displaystyle (2)&xet; képletnek. Ebből a képletből behelyettesítéssel látható, hogy &tex;\displaystyle (*)&xet; fennállása nem függ a négy kör sugarától, csupán a négy érintési pont helyzetétől. Vagyis vehetjük a köröket ponttá fajulónak, és ezzel a Ptolemaiosz-tételre vezettük vissza a Casey-t.
Igazából Sharygin szerint lehetünk ügyesebbek is: egy mozdulattal mind a Casey-tételt, mint speciális esetét, a Ptolemaiosz-tételt is levezethetjük, ha a négy körsugarat inkább úgy vesszük fel, hogy &tex;\displaystyle \alpha&xet; és &tex;\displaystyle \delta&xet; ponttá fajuljon és &tex;\displaystyle \beta,\gamma&xet; az &tex;\displaystyle AD&xet; húrt érintse. Ekkor a &tex;\displaystyle (*)&xet;-beli mennyiségek mind az &tex;\displaystyle AD&xet; szakaszon jelennek meg, és ezekre &tex;\displaystyle (*)&xet;-ot már gyerekjáték ellenőrizni.
A Casey-tétel akkor is igaz marad, ha &tex;\displaystyle k&xet; nem kör, hanem egyenes. Sőt, éppen ugyanaz a triviális állítás, mint az, amit az imént &tex;\displaystyle AD&xet; húron megjelenítettünk.
A megfordítás pedig klasszikus tételmegfordítás: magát a tételt használó indoklása van.
Mindenekelőtt jegyezzük meg, hogy &tex;\displaystyle (1)&xet; szerint ha mind a négy irányított körünk sugarát ugyanazzal a mennyiséggel változtatjuk, azzal minden közös érintőszakasz ugyanakkora marad, és közben jól láthatóan a négy kört érintő irányított kör (vagy egyenes) léte sem csorbul. Emiatt változathatjuk a körsugarakat úgy, hogy mondjuk &tex;\displaystyle \alpha&xet; egyetlen &tex;\displaystyle A&xet; ponttá fajuljon.
Hogyha a &tex;\displaystyle \beta,\gamma,\delta&xet; körök ekkor szintén pontok lesznek, akkor a Ptolemaiosz-tétel megfordítása miatt készen vagyunk. Egyéb esetben pedig az apollóniuszi probléma miatt van két különböző irányított kör (vagy egyenes), ami &tex;\displaystyle \beta,\gamma,\delta&xet; mindegyikét érinti: legyenek ezek &tex;\displaystyle k_1&xet; és &tex;\displaystyle k_2&xet;.
Vezessük be még a &tex;\displaystyle \lambda=\frac{t_{A\beta}}{t_{A\delta}}&xet; és &tex;\displaystyle \mu=\frac{t_{A\gamma}}{t_{A\delta}}&xet; jelölést. Ekkor a feltétel szerint
&tex;\displaystyle \mu=\frac{t_{A\gamma}}{t_{A\delta}}=\frac{t_{A\beta}t_{\gamma\delta}+t_{A\delta}t_{\beta\gamma}}{t_{A\delta}t_{\beta\delta}}=\frac{\lambda t_{\gamma\delta}+t_{\beta\gamma}}{t_{\beta\delta}}.&xet;
A Hraskó-féle koaxális körös lemma szerint &tex;\displaystyle A&xet; rajta van azon az &tex;\displaystyle \ell&xet; körön/egyenesen, amit a &tex;\displaystyle \lambda&xet; arány és &tex;\displaystyle \beta,\delta&xet; kör meghatároz, illetve azon az &tex;\displaystyle m&xet; körön/egyenesen, amit &tex;\displaystyle \mu&xet; arány és &tex;\displaystyle \gamma,\delta&xet; kör meghatároz.
Tegyük össze a két előbbi definíciót! Az &tex;\displaystyle \ell&xet; és &tex;\displaystyle k_1&xet; két pontban metsz, hisz &tex;\displaystyle k_1&xet; érinti &tex;\displaystyle \beta&xet;-t és &tex;\displaystyle \delta&xet;-t. Az is igaz, hogy éppen az egyik metszéspont a &tex;\displaystyle k_1&xet; kör azon ívére esik, ami nem tartalmazza a &tex;\displaystyle k_1&xet;-nek &tex;\displaystyle \gamma&xet;-val való érintési pontját. Legyen ő &tex;\displaystyle A_1&xet;. Ez azért használ, mert a Casey-tételt felírhatjuk:
&tex;\displaystyle t_{A_1\gamma}t_{\beta\delta}=t_{A_1\beta}t_{\gamma\delta}+t_{A_1\delta}t_{\beta\gamma},&xet;
&tex;\displaystyle \frac{t_{A_1\gamma}}{t_{A_1\delta}}=\frac{\lambda t_{\gamma\delta}+t_{\beta\gamma}}{t_{\beta\delta}}=\mu,&xet;
vagyis &tex;\displaystyle A_1\in m&xet;. Hasonlóan felvéve &tex;\displaystyle k_2&xet;-n az &tex;\displaystyle A_2&xet; pontot, elmondható, hogy &tex;\displaystyle A_2\in \ell&xet;-ből &tex;\displaystyle A_2\in m&xet; következik.
Tehát &tex;\displaystyle A,A_1,A_2&xet; három pont, ami &tex;\displaystyle \ell\cap m&xet; metszetbe tartozik. Két kör/egyenes legfeljebb két pontban metszhet, ezért vagy &tex;\displaystyle A&xet; egybeesik &tex;\displaystyle A_1,A_2&xet; egyikével és készen vagyunk, vagy pedig marad a kellemetlen &tex;\displaystyle A_1=A_2&xet; eset.
Azt az esetet, hogy &tex;\displaystyle A_1=A_2&xet;, azzal gyógyíthatjuk, hogy észrevesszük, hogy ilyenkor &tex;\displaystyle \ell&xet; és &tex;\displaystyle m&xet; érintkeznek, és úgy &tex;\displaystyle A=A_1=A_2&xet; következik. Azért lesz &tex;\displaystyle \ell&xet; és &tex;\displaystyle m&xet; érintő, mert ha &tex;\displaystyle \lambda&xet;-t lecseréljük valami &tex;\displaystyle \lambda’\to \lambda&xet;-ra, úgy a kapott &tex;\displaystyle A_1’&xet; és &tex;\displaystyle A_2’&xet; pontok már különbözőek, és ez a két különböző metszéspontja a nyert &tex;\displaystyle \ell’&xet; és &tex;\displaystyle m’&xet; görbéknek; mivel &tex;\displaystyle A_1’&xet; és &tex;\displaystyle A_2’&xet; is az &tex;\displaystyle A_1=A_2&xet;-höz fog tartani, ezért &tex;\displaystyle \ell&xet; és &tex;\displaystyle m&xet; „mindkét metszéspontja” &tex;\displaystyle A_1=A_2&xet;, vagyis érintkeznek. (Ez ilyenformán meggyőző érvelésnek hangzik, de precizzé tehető.)
A bizonyítás ezzel pedig véget ért.
|
|
| [1894] w | 2016-01-24 00:14:41 |
 Leírom saját tolmácsolásomban a Casey-tételt és megfordítását, bizonyítással együtt.
Az "oda irány" az angol Wikipédián látott bizonyítás diszkusszióval való helyessé tételével adódott. A megfordítás bizonyítása a Sharygin: Problems in Plane Geometry c. könyvben található meg.
Sajnálom, ábrá(ka)t nem csatolok, az Olvasónak papírt és rajzszerszámot kell majd ragadnia, ha nem kívánja fejben elképzelni az ábrákat.
Szükségünk lesz az irányított kör fogalmára. Egy irányított kör egy kör a síkon, amihez egy &tex;\displaystyle \epsilon\in\{1,-1\}&xet; előjelet rendelünk. Azt mondjuk, hogy az irányított kör sugara &tex;\displaystyle R=\epsilon |R|&xet;, ahol &tex;\displaystyle |R|&xet; a szokásos értelemben vett sugár. Azt mondjuk, hogy &tex;\displaystyle x,y&xet; irányított körök érintik egymást, hogyha irányítatlan köreik belülről érintik egymást és &tex;\displaystyle x,y&xet; azonos irányítású, vagy pedig kívülről érintik egymást és &tex;\displaystyle x,y&xet; ellentétes irányítású. (Például: egybeeső körök belülről érintik egymást, ezért azonos irányításnál érintőek, különböző irányításnál nem. Egy ponttá fajuló kör irányítása mindegy, mert &tex;\displaystyle 0&xet; a sugara.)
Jelölje még &tex;\displaystyle x,y&xet; irányított körökhöz &tex;\displaystyle t_{xy}&xet; az &tex;\displaystyle x&xet; és &tex;\displaystyle y&xet; körök közös „külső” érintőszakaszának a hosszát. Vagyis ha &tex;\displaystyle x,y&xet; azonos irányítású, a külső érintőszakaszt, ha különböző irányítású, a belső érintőszakaszt kell venni.
Legyen &tex;\displaystyle x,y&xet; irányított körök középpontja &tex;\displaystyle O_x,O_y&xet;, sugara &tex;\displaystyle R_x,R_y&xet;. Ekkor Pitagorasz-tétel szerint
| &tex;\displaystyle t_{xy}=\sqrt{O_xO_y^2+(R_x-R_y)^2},&xet; | (1) |
és ebből levezethető, hogy ha &tex;\displaystyle x,y&xet; rendre az &tex;\displaystyle X,Y&xet; pontban érint egy &tex;\displaystyle R_k&xet; sugarú irányított &tex;\displaystyle k&xet; kört, akkor
| &tex;\displaystyle t_{xy}=\sqrt{\left(1-\frac{R_x}{R_k}\right)\left(1-\frac{R_y}{R_k}\right)} \cdot |XY|.&xet; | (2) |
Fontos még az apollóniuszi problémáról szót ejteni. Tulajdonképpen következik belőle, hogy ha adott három irányított kör, &tex;\displaystyle x,y,z&xet;, melyek valamelyikének nem nulla a sugara, akkor két olyan irányított kör is adható, melyek &tex;\displaystyle x,y,z&xet; mindegyikét érintik.
Még egy lemmát használunk, amit koaxális körök lemmájaként is hallottam, bár én elsőként ebben a cikkben láttam, nevezetesen hogy ha adott két kör, akkor az olyan pontok halmaza, melyekre a két körhöz húzott érintők hosszainak aránya &tex;\displaystyle \lambda&xet;, kör, ha &tex;\displaystyle \lambda\neq 1&xet;, és épp a hatványvonal, ha &tex;\displaystyle \lambda=1&xet;. (Amúgy ha a két körünk ponttá fajul, épp a pontok Apollóniusz-köreit kapjuk.)
Ennyi bevezetés után rátérek a két állítás kimondására.
|
|
| [1893] Sinobi | 2016-01-23 21:43:39 |
 Sawayama => egy &tex;\displaystyle ABC&xet; háromszög két oldalát érintő kör pontosan akkor érinti a &tex;\displaystyle k&xet; körülírt körét is, ha az érintési pontok tükrösek a beírt kör &tex;\displaystyle I&xet; középpontjára.
Ez alapján: t tükörképe I-re átmegy U-n, tehát átmegy Z-n is, ezt akartuk belátni.
|
 |
| Előzmény: [1890] sakkmath, 2015-12-21 02:01:39 |
|
| [1892] w | 2016-01-23 11:18:59 |
 Megpróbálom hamarosan leírni a preciz kimondását a tételnek és a megfordításnak. Van bizonyítás is hozzájuk. (Szeretném viszont az irányításokat is rendbetenni.)
|
| Előzmény: [1891] HoA, 2016-01-22 16:42:16 |
|
| [1891] HoA | 2016-01-22 16:42:16 |
 Mit értesz megfordításon? Ahogy én ismerem, ez a tétel adott módon érintkező 1 + 4 kör közös érintőszakaszai közötti méretes összefüggést állít. Mi ennek a megfordítottja?
|
| Előzmény: [1889] sakkmath, 2015-12-13 13:13:22 |
|
| [1890] sakkmath | 2015-12-21 02:01:39 |
 188. feladat: Adott egy &tex;\displaystyle k&xet; kör az &tex;\displaystyle AB&xet; húrral, s annak &tex;\displaystyle U&xet; felezéspontjával. Legyen adott a &tex;\displaystyle k_1&xet; kör úgy, hogy érintse az &tex;\displaystyle AB&xet; szakaszt &tex;\displaystyle U&xet;-ban és érintse a &tex;\displaystyle k&xet; kört. A &tex;\displaystyle k_1&xet; kör &tex;\displaystyle A&xet;-n átmenő, &tex;\displaystyle AB&xet;-től különböző érintőjét jelöljük &tex;\displaystyle t&xet;-vel. A &tex;\displaystyle k&xet; kör és &tex;\displaystyle t&xet; &tex;\displaystyle A&xet;-tól különböző metszéspontja &tex;\displaystyle C&xet;, a &tex;\displaystyle BC&xet; szakasz felezéspontja &tex;\displaystyle Z&xet;. Tekintsük azt a &tex;\displaystyle k_2&xet; kört, amelyik a &tex;\displaystyle BC&xet; egyenest &tex;\displaystyle Z&xet;-ben érinti és érinti az &tex;\displaystyle AC&xet; egyenest. Bizonyítsuk be, hogy &tex;\displaystyle k_2&xet; és &tex;\displaystyle k&xet; érinti egymást.
|
|
| [1889] sakkmath | 2015-12-13 13:13:22 |
 Létezik-e a Casey-tétel megfordításának elemi geometriai bizonyítása?
|
|
| [1888] Sinobi | 2015-10-29 11:11:13 |
 Aha. És az igaz-e, hogy a köréírt körük középpontja is egyenletesen, egyenesen mozog? (például limeszben mozoghat egyenesen, hogy egyébként hiperbola/harmadrendű a mértani helye)
Ha nem ajánlasz mást, akkor a 187. feladat legyen egy szokásos, szimpla egyeneses-távolságos (csak mert az én megoldásom ronda, és nem találok szépet):
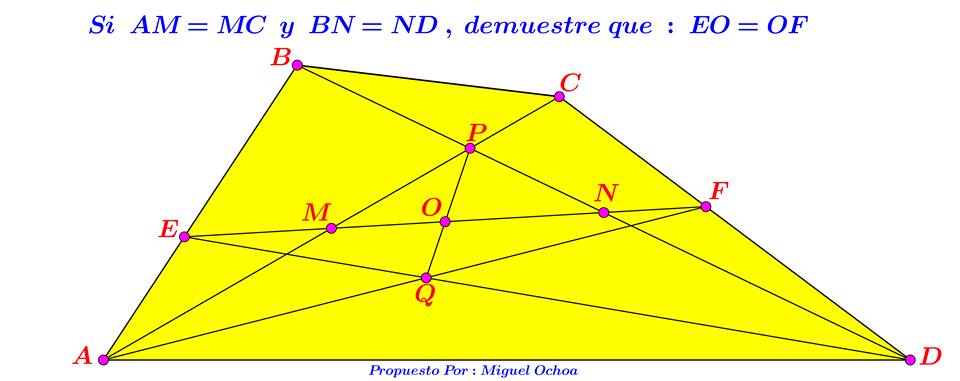
&tex;\displaystyle ABCD&xet; négyszögben &tex;\displaystyle M&xet;,&tex;\displaystyle N&xet; &tex;\displaystyle :=&xet; mid(&tex;\displaystyle AC&xet;), mid(&tex;\displaystyle BD&xet;); &tex;\displaystyle E&xet;,&tex;\displaystyle F&xet; &tex;\displaystyle :=&xet; &tex;\displaystyle MN \cap AB&xet;, &tex;\displaystyle MN \cap CD&xet;; &tex;\displaystyle P&xet; &tex;\displaystyle :=&xet; &tex;\displaystyle AC \cap BD&xet;; &tex;\displaystyle Q&xet; &tex;\displaystyle :=&xet; &tex;\displaystyle ED \cap AF&xet;, (lásd ábra), bizonyítsd be, hogy &tex;\displaystyle QP&xet; felezi az &tex;\displaystyle EF&xet; szakaszt.
Aztán, valaki ajánljon mást (mondjuk, aki megoldja).
|
 |
| Előzmény: [1887] Fálesz Mihály, 2015-10-26 15:34:28 |
|
| [1887] Fálesz Mihály | 2015-10-26 15:34:28 |
 Ebben a formában nem igaz. Például, ha a négy pont &tex;\displaystyle A(t)=(-t,0)&xet;, &tex;\displaystyle B(t)=(t,0)&xet;, &tex;\displaystyle C(t)=(2t,1)&xet; és &tex;\displaystyle D(t)=(-2t,1)&xet;, akkor &tex;\displaystyle t=0&xet; esetén két-két pont egybeesik, &tex;\displaystyle t\ne0&xet; esetén pedig a négy pont egy szimmetrikus trapéz csúcsai. A négy pont tehát mindig egy körön van. Ugyanakkor a négy sebességvektor &tex;\displaystyle (-1,0)&xet;, &tex;\displaystyle (1,0)&xet;, &tex;\displaystyle (2,0)&xet; és &tex;\displaystyle (-2,0)&xet; egy egyenesre esik.
Az viszont igaz, hogy a négy sebességvektor egy körre vagy egy egyenesre esik. Ha valamelyik két sebességvektor egyenlő, akkor a sebességvektorok triviálisan egy körön vagy egyenesen vannak. Tegyük tehát fel, hogy a négy sebességvektor különböző. Tekintsük a pontokat komplex számoknak, és vizsgáljuk a
&tex;\displaystyle
\big(A(t),B(t),C(t),D(t)\big) =
\frac{C(t)-A(t)}{B(t)-C(t)}:\frac{D(t)-A(t)}{B(t)-D(t)}
&xet;
kettősviszony határértékét, ha &tex;\displaystyle t\to\infty&xet;. A négy pont akkor és csak akkor van egy körön vagy egy egyenesen, ha a kettősviszony nem értelmes, mert valamelyik két pont egybeesik (ilyen legfeljebb 4 pillanatban történhet), vagy a kettősviszony tisztán valós. A ketősviszony tehát véges sok ponttól eltekintve valós, így a határértéke is tisztán valós. A határértéke viszont éppen a sebességvektorokból készített kettősviszony:
&tex;\displaystyle
\lim_{t\to\infty} \big(A(t),B(t),C(t),D(t)\big) =
\lim_{t\to\infty}\frac{\frac{C(t)}t-\frac{A(t)}t}{\frac{B(t)}t-\frac{C(t)}t}:\frac{\frac{D(t)}t-\frac{A(t)}t}{\frac{B(t)}t-\frac{D(t)}t} =
\frac{C'-A'}{B'-C'}:\frac{D'-A'}{B'-D'} =
(A',B',C',D'),
&xet;
így ez is valós, tehát a négy sebességvektor, &tex;\displaystyle A'&xet;, &tex;\displaystyle B'&xet;, &tex;\displaystyle C'&xet; és &tex;\displaystyle D'&xet; egy körön vagy egy egyenesen van.
|
| Előzmény: [1886] Sinobi, 2015-10-24 10:24:25 |
|
| [1886] Sinobi | 2015-10-24 10:24:25 |
 186. feladat: Igaz-e, hogy ha 4 pont egyenletes sebességgel mozog a síkon úgy, hogy minden t időpillanatban egy körre esnek, akkor a sebességvektoraik végpontjai is egy körre esnek?
|
|