|
| [1934] Erben Péter | 2021-06-07 14:39:58 |
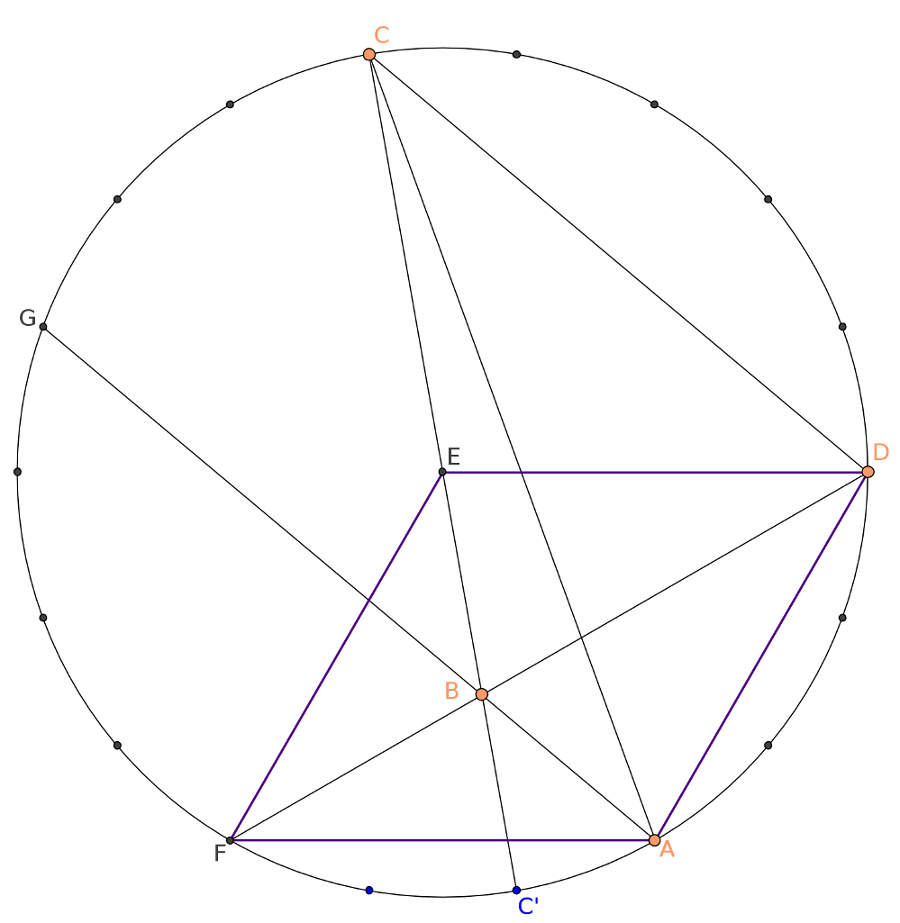
 A feladat egy lehetseges eredete a szabalyos 18-szog atloinak az a tulajdonsaga, hogy egymassal bezart szoguk mindig a 10 fok egesz tobbszorose.
Ha \(\displaystyle C\), \(\displaystyle D\) es \(\displaystyle A\) egy szabalyos 18-szog megfelelo csucsai, akkor \(\displaystyle E\) eppen a sokszog kozeppontja.
A kozbulso lepes, hogy a \(\displaystyle CC'\), \(\displaystyle AG\) es \(\displaystyle DF\) atlok egy ponton mennek at, ami peldaul visszavezetheto arra, hogy \(\displaystyle EDAF\) egy rombusz, amelynek szogei 120 fok es 60 fok.
Mindez persze nem a feladat megoldasa, inkabb azt mutatja, hogyan "keszulhetett" a kerdes.
|
 |
| Előzmény: [1933] Lpont, 2021-06-07 12:32:53 |
|
| [1933] Lpont | 2021-06-07 12:32:53 |
 I. Szögszámolással adódik, hogy BD felezi az ABCD négyszög B-nél levő szögét.
II. A-t tükrözve BD-re a kapott E pont rajta van BC egyenesén és AD=ED.
III. Újabb szögszámolás után EDC háromszög egyenlő szárú, ED=EC.
IV. Harmadjára is szögeket számolva EC=EA, tehát AE=EC=ED=AD, azaz AED háromszög szabályos, minden szöge 6alfa, így alfa=10fok.
|
| Előzmény: [1932] rezes, 2021-06-06 13:18:23 |
|
| [1932] rezes | 2021-06-06 13:18:23 |
 \(\displaystyle ABCD\) konvex négyszögben \(\displaystyle BC=CD, BAC\sphericalangle=3\alpha\), \(\displaystyle BCA\sphericalangle=\alpha,\) \(\displaystyle ACD\sphericalangle=3\alpha\), \(\displaystyle DAC\sphericalangle=5\alpha.\) Mennyi \(\displaystyle \alpha\) értéke?
|
|
| [1931] HoA | 2021-02-03 12:52:03 |
 Bocsánat, elírás. Helyesen:
A \(\displaystyle D_0D_1F_1\) és \(\displaystyle D_0D_2F_2\) háromszögek hasonlók, \(\displaystyle D_0, F_1 és F_2\) egy egyenesen vannak.
|
| Előzmény: [1930] HoA, 2021-02-03 12:34:31 |
|
| [1930] HoA | 2021-02-03 12:34:31 |
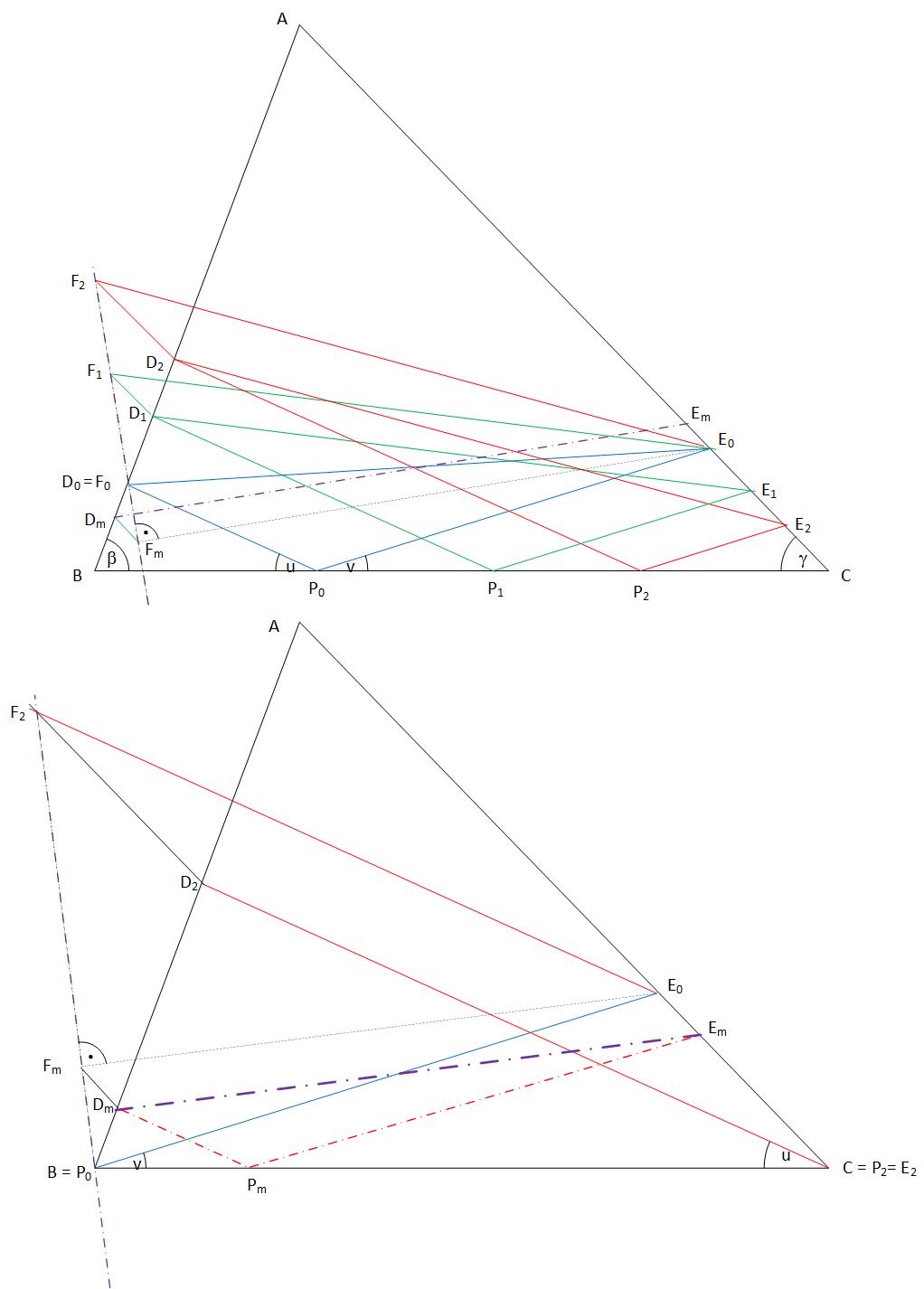
 Legyen \(\displaystyle P\) egyik helyzete \(\displaystyle P_0\). Rajzoljuk meg az ehhez tartozó \(\displaystyle P_0D_0\) és \(\displaystyle P_0E_0\) szakaszokat. P egy másik, \(\displaystyle P_1\) helyzetéhez tartozzanak A \(\displaystyle D_1\) és \(\displaystyle E_1\) pontok. A párhuzamos szelők tétele szerint \(\displaystyle BP_0 D_0\) háromszögből \(\displaystyle D_0D_1 = k P_0P_1\) , ahol \(\displaystyle k = \frac{sin u}{sin(\beta + u)}\) . Hasonlóan a \(\displaystyle P_0CE_0\) háromszögből \(\displaystyle E_0E_1 = m P_0P_1\) , ahol \(\displaystyle m = \frac{sin v}{sin(\gamma + v)}\) . Toljuk el \(\displaystyle E_1D_1\) -et önmagával párhuzamosan az \(\displaystyle AC\) egyenes mentén úgy, hogy \(\displaystyle E_1\) \(\displaystyle E_0\) -ba kerüljön. \(\displaystyle D_1\) új helyzete legyen \(\displaystyle F_1\) . \(\displaystyle D_1E_1E_0F_1\) paralelogramma, \(\displaystyle D_1F_1 \# E_1E_0\) , \(\displaystyle \frac{D_0D_1}{D_1F_1} = \frac {k}{m}\). Ismételjük meg egy további \(\displaystyle P_2\) pontra a \(\displaystyle P_1\) -re elvégzetteket. Kapjuk a \(\displaystyle D_2 , E_2, F_2\) pontokat. \(\displaystyle \frac{D_0D_2}{D_2F_2} = \frac {k}{m}\). A \(\displaystyle D_0D_1F_1\) és \(\displaystyle D_0D_2F_2\) háromszögek hasonlók, \(\displaystyle D_0, D_1 és D_2\) egy egyenesen vannak. A megfelelő \(\displaystyle D_iE_i\) szakasszal párhuzamos és azonos hosszúságú \(\displaystyle F_iE_0\) szakaszok egyik végpontja közös (\(\displaystyle E_0\)) , a másik az \(\displaystyle F_iF_j\) egyenesen mozog. Közülük a legrövidebb az \(\displaystyle E_0\) -ból az \(\displaystyle F_iF_j\) -re bocsátott merőleges \(\displaystyle F_m\) talppontját \(\displaystyle E_0\) -lal összekötő szaksz lesz. A keresett legrövidebb \(\displaystyle DE\) szakaszt akkor kapjuk, ha \(\displaystyle E_0F_m\) -et az \(\displaystyle AC\) egyenes mentén úgy toljuk el, hogy \(\displaystyle F_m\) az \(\displaystyle AB\) egyenesre essék, a szakasz végpontjai legyenek \(\displaystyle D_m és E_m\)
A szerkesztést úgy hajthatjuk végre a legkevesebb vonal megrajzolásával, ha P két szélső helyzetét használjuk. Legyen tehát \(\displaystyle P_0 = B, P_2=C\) , \(\displaystyle E_0\) az \(\displaystyle AC\) oldalnak az a pontja, melyre \(\displaystyle E_0BC \angle = v\) , \(\displaystyle D_2\) az \(\displaystyle AB\) oldalnak az a pontja, melyre \(\displaystyle D_2CB \angle =u\) . \(\displaystyle CD_2\) -t \(\displaystyle CA\) mentén úgy eltolva, hogy \(\displaystyle C\) \(\displaystyle E_0\) -ba jusson \(\displaystyle D_2\) kerüljün \(\displaystyle F_2\) -be .\(\displaystyle E_0\) -ból az \(\displaystyle F_2B\) egyenesre bocsátott merőleges talppontja legyen \(\displaystyle F_m\) . A legrövidebb DE szakaszt \(\displaystyle E_0F_m\) -nek \(\displaystyle AC\) -vel párhuzamos eltolásával kapjuk úgy, hogy \(\displaystyle F_m\) az \(\displaystyle AB\) egyenesen lévő \(\displaystyle D_m\) -be kerüljön, \(\displaystyle E_0\) pedig \(\displaystyle E_m\) -be.
Ujjgyakorlatnak hagyjuk annak bizonyítását, hogy a \(\displaystyle D_m\) -ből \(\displaystyle D_2C\) -vel húzott párhuzamos és az \(\displaystyle E_m\) -ből \(\displaystyle E_0B\) vel húzott párhuzamos egy, a \(\displaystyle BC\) egyenesen fekvő, feladatunk megoldását adó \(\displaystyle P_m\) pontban metszik egymást.
|
 |
| Előzmény: [1929] sakkmath, 2021-01-21 23:58:57 |
|
| [1929] sakkmath | 2021-01-21 23:58:57 |
 A 192. feladat valóban nyitott. Talán ezért (is) nagyon nehéz, de megoldható. Az általam ismert megoldást nyolc éve publikálták, azóta a közlés helyén, egy közismert, frekventált oldalon, állócsillagként ragyog: még nem reagált rá senki – legalábbis ott nem. Ebből arra következtetek, hogy máig csak ez az egy megoldás létezik. Ez a dolgozat – a szerkesztéses részét tekintve – mindvégig euklideszi szerkesztésekkel jut el a \(\displaystyle P\) pont keresett pozíciójához.
Beírom a lényegesen könnyebb,193. feladatot is, amely csak u és v szerepét tekintve különbözik a rokon 192.-től. Találjunk euklideszi szerkesztést alkalmazó megoldást a következő, 193. feladatra:
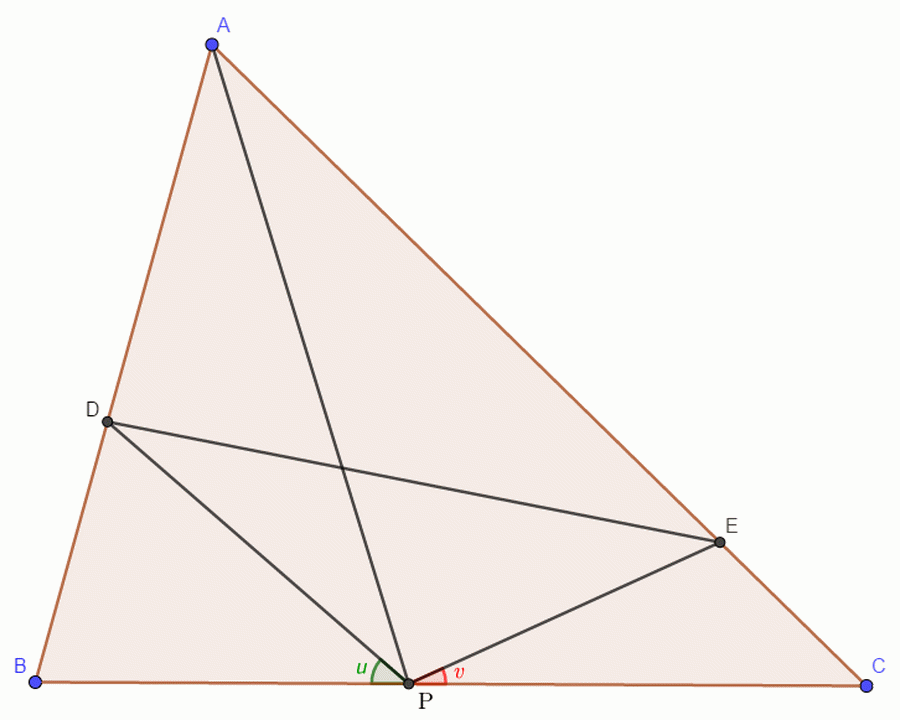
Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalán mozog egy \(\displaystyle P\) pont. Az \(\displaystyle AB\) oldal \(\displaystyle D\), valamint az \(\displaystyle AC\) oldal \(\displaystyle E\) pontjára fennáll, hogy rögzített e két szög: \(\displaystyle u=BPD∠\) és \(\displaystyle v=CPE∠\). Keressük meg a \(\displaystyle P\) pont azon helyzetét, amelyre a \(\displaystyle DE\) szakasz hossza minimális!
|
 |
| Előzmény: [1928] Sinobi, 2021-01-19 18:24:05 |
|
| [1928] Sinobi | 2021-01-19 18:24:05 |
 Nagyon nyitott a feladat, és nekem kételyeim is vannak azzal kapcsolatban, hogy van értelmes, szép válasz. Az ennél egyszerűbbnek tűnő
Philo szelő probléma: adott egy szög és benne egy pont, keressük meg a legrövidebb szakaszt, amely átmegy a ponton, és a végpontjai a szög két szárán van
sem szerkeszthető már körzővel és vonalzóval. Bár az például megoldható olyan eszközzel, amelyik megadja két kúpszelet metszéspontjait.
|
|
| [1927] sakkmath | 2021-01-13 23:43:55 |
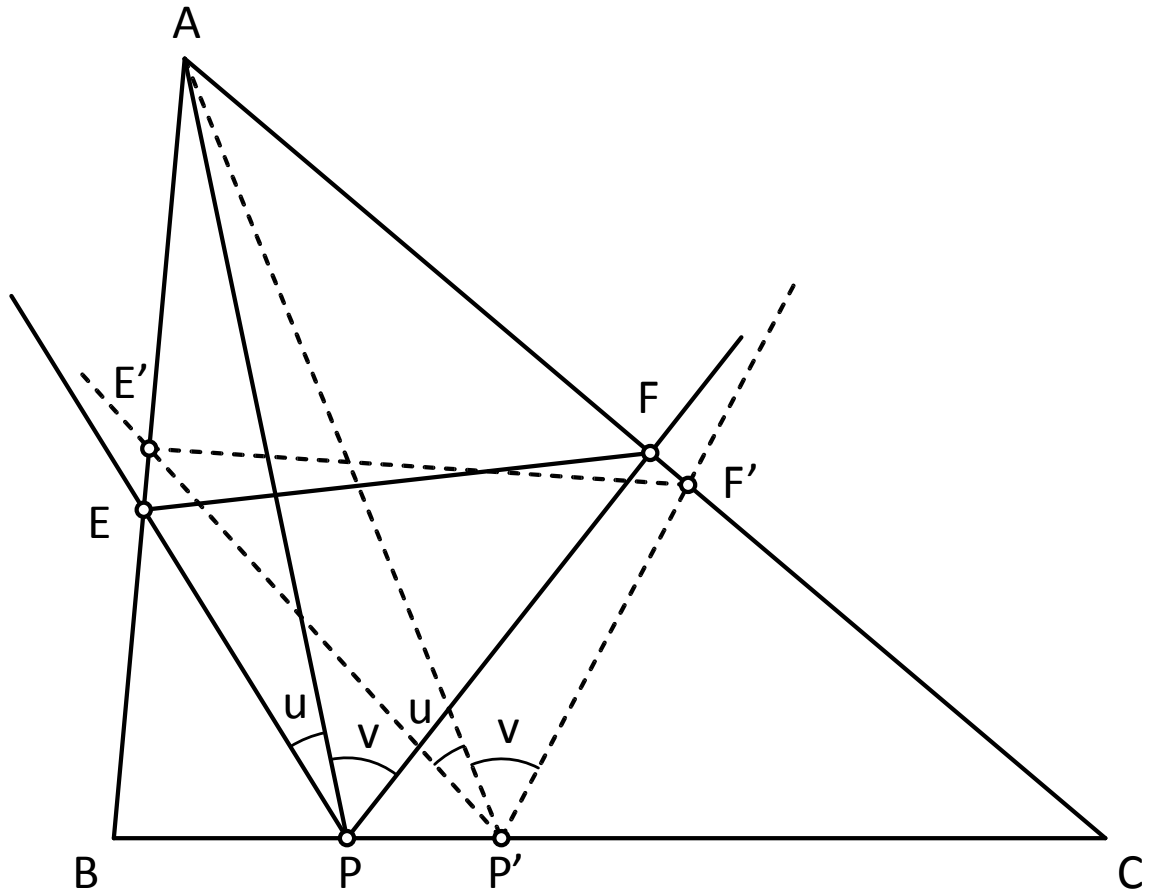
 \(\displaystyle {\bf 192.}\) \(\displaystyle {\bf feladat}\): Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalán mozog egy \(\displaystyle P\) pont. Az \(\displaystyle AB\) oldal \(\displaystyle E\), valamint az \(\displaystyle AC\) oldal \(\displaystyle F\) pontjára fennáll, hogy konstans az \(\displaystyle u = EPA\angle\) és a \(\displaystyle v = APF\angle\). Keressük meg a \(\displaystyle P\) pont azon helyzetét, amelyre az \(\displaystyle EF\) szakasz hossza minimális!
|
 |
|
| [1926] HoA | 2019-12-06 14:58:36 |
 Mit nevezzünk helytállónak? A módszer körívekből állít össze egy, az ellipszist közelítő görbét. Megvizsgálhatjuk például, a megfelelő tengelyeket egymásra fektetve a tengelyek hosszának függvényében a nagytengely pontjait abszcisszáknak, az ellipszis ill. a közelítő görbe hozzárendelt pontjait ordinátáknak tekintve, mennyi az ordináták eltérésének maximuma. Vagy mekkora a két görbe közötti területdarabok "vastagsága" . Te mire gondoltál ?
|
| Előzmény: [1925] TTibi, 2019-12-04 16:55:34 |
|
|
| [1924] Sinobi | 2017-05-21 13:05:29 |
 Adott egy kör, és rajta kívül két pont. A pontokból érintőket húzunk a körhöz. Igazold, hogy a négy érintési pont a két ponttal egy kúpszeletre esik. Igazold továbbá, hogy ennek a kúpszelet egy pontjából ha a körhöz húzunk érintőt, és így csináljuk a Poncelet tételben szereplő eljárást, akkor 4 lépés után záródik.
(könnyű)
|
|
| [1923] Vonka Vilmos Úr | 2017-04-26 13:40:54 |
 A fókuszok valós eszközökkel is szépen kezelhetőek: kúpszelet fókusza olyan pont, amelyre illeszkedő konjugált egyenespárok pontosan a merőleges egyenespárok.
Komplex módszerekkel is meg lehet őket fogni: az abszolút képzetes körpontokból érintőket húzunk a kúpszelethez, ezek páronként vett további metszéspontjai a fókuszok. Így a két valós fókusz mellett egy képzetes fókuszpár is adódik.
|
| Előzmény: [1922] Sinobi, 2017-04-26 09:42:48 |
|
| [1922] Sinobi | 2017-04-26 09:42:48 |
 Aham. A gyengébb állítás, amelyben két egyenesre kell esniük, az itt található tétel2-nek a Minkowski geometriában való felírása, az erősebb állítás, amelyben az is elég ha kúpszeletre esnek, pedig a de Sitter geometriában (ahol a szög és a távolságmérés is hiperbolikus) való kimondása.
Kúpszeletek fókuszai kezelhetők szépen egyszerűen komplex projektív módszerekkel? (ebben a két geometriában valós projektív eszközökkel is megfoghatók a fókuszpontok)
|
| Előzmény: [1921] Vonka Vilmos Úr, 2017-03-27 08:07:20 |
|
| [1921] Vonka Vilmos Úr | 2017-03-27 08:07:20 |
 Kúpszeletsorokra vonatkozó számolásokkal (amik nem túl nehezek, csak kúpszeletek egyenleteiből kell lineárisan kikombinálgatni a kúpszeletsoruk további kúpszeleteinek egyenletét) egy kicsit általánosabbat is be tudok látni:
Ha adott három kúpszelet úgy, hogy közülük bármely kettőnek két metszéspontja egy negyedik kúpszeleten van (ez most esetünkben egy metsző egyenespár), akkor a további két metszéspont-párok összekötő egyenesei konkurrensek.
De még jó lenne erre valami szebb bizonyítást keresni (szerintem algebrai görbék fokszámát vizsgálva, mint az eredeti "kalapács" esetén a Cayley-Bacharach tételes szép bizonyítás, ki kéne jönnie).
|
| Előzmény: [1920] Sinobi, 2017-03-26 16:09:26 |
|
| [1920] Sinobi | 2017-03-26 16:09:26 |
 Ha a nagy négyzetbe is ellipszist írunk, majd azt dualizáljuk, akkor az előző kalapácshoz nagyon hasonló állítást kapunk: adott két egyenesen 3-3 pont, ezeken át 3 kúpszelet úgy, hogy bármelyik 2-nek 4 metszéspontja legyen, bizonyítsuk be hogy a hatványvonalak 1 ponton mennek át.
Azt hogyan látnád be, ha nem ezt akarnád dualizálni?
(azt ebből tudjuk, hogy mint konfiguráció azonos az előbbi kalapáccsal, vagyis a PG téma 126-ik hozzászólásával, de mondjuk ez nem tűnik fel; meg nem is látom most hogy mi hova kerül)
|
| Előzmény: [1918] Vonka Vilmos Úr, 2017-03-25 17:10:09 |
|
| [1919] Sinobi | 2017-03-25 18:42:14 |
 Kalapács és szög :D Tetszik :)
|
|
| [1918] Vonka Vilmos Úr | 2017-03-25 17:10:09 |
 Na jó, ezt elismerem, hogy kicsit elkapkodtam. (Attól még, hogy a kollineáció az egyik téglalapot a másikba viszi, nem biztos, hogy a beírt kúpszeletet is éppen a tekintett másikba viszi át.)
Újabb próbálkozás:
A másik fórumban beszéltünk a következő állításról: Ha három kúpszeletnek van két közös pontja, akkor a további két-két metszéspontot összekötő egyenesek konkurrensek.
Nézzük ennek az állításnak a duálisát: Ha három kúpszeletnek van két közös érintője, akkor a további két-két közös érintők metszéspontjai kollineárisak.
Legyen most két kúpszeletünk a két beírt ellipszis. A harmadik pedig az az elfajuló másodosztályú görbe, a négyzet két oldalirányának végtelen távoli pontjából áll. A két pontból álló elfajuló másodosztályú görbe érintői a két pontra illeszkedő összes egyenes (ez a metsző egyenespár duálisa).
Erre a három görbére alkalmazva az előbb megfogalmazott duális állítást éppen a feladat állítása adódik.
|
| Előzmény: [1917] Sinobi, 2017-03-25 01:34:01 |
|
|
| [1916] Vonka Vilmos Úr | 2017-03-24 21:58:41 |
 A két befoglaló téglalapnak a négyzet oldalain levő megfelelő csúcsait összekötő egyenesek éppen a négyzet átlóján metszik egymást (ez a Papposz-tételből könnyen látható), legyen ez a közös pont \(\displaystyle C\). Ez azt jelenti, hogy \(\displaystyle C\) centrumú kollineációval át lehet vinni az egyik kis téglalapot a másikba. Ez a kollineáció az egyik téglalapba írt ellipszist a másik téglalapba írt ellipszisbe viszi. Így a közös érintők invariáns egyenesek, vagyis átmennek a \(\displaystyle C\) centrumon.
|
| Előzmény: [1914] Sinobi, 2017-03-24 18:13:28 |
|
|
| [1914] Sinobi | 2017-03-24 18:13:28 |
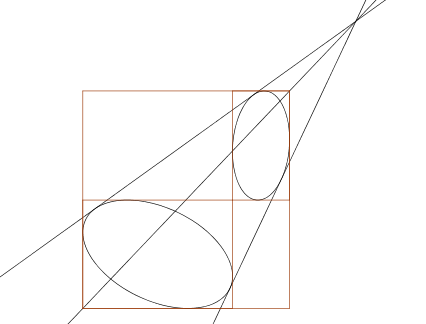
 191. Feladat Egy négyzetet felosztunk 4 részre, két szemközti részbe ellipsziseket írunk az ábra szerint. Bizonyítsd be, hogy a két ellipszis két másik közös érintőjének a metszése a négyzet átlóján van.
|
 |
|
|
| [1912] Cogito | 2016-11-25 22:57:41 |
 A feladatot 1955. január 2-án az alábbi formában adták fel az – akkor még Rákosi Mátyásról elnevezett – Országos Tanulmányi Versenyen:
Egy háromszög belsejében felvett tetszőleges ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszög területét hat részre osztják. Mekkora az adott háromszög területe, ha adva van a keletkezett 3 háromszög területe: \(\displaystyle t_1\), \(\displaystyle t_2\), \(\displaystyle t_3\) ?
Érdemes ezt az általánosított feladatot is megoldani.
|
| Előzmény: [1908] Gergely99, 2016-11-22 21:10:01 |
|
| [1911] Gergely99 | 2016-11-23 23:11:49 |
 Elnézést kérek. Későn esett le a dolog. Nem aktuális a kérdés, és nagyon szépen köszönöm a választ :)
|
|














