|
|
| [210] Hraskó András | 2005-03-01 23:40:11 |
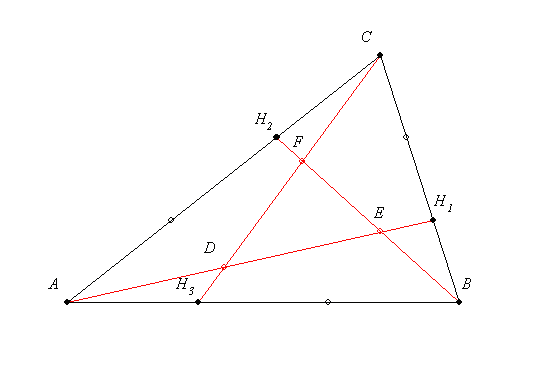
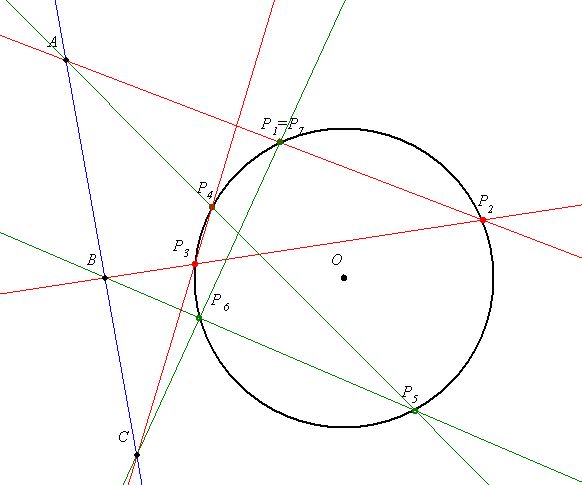
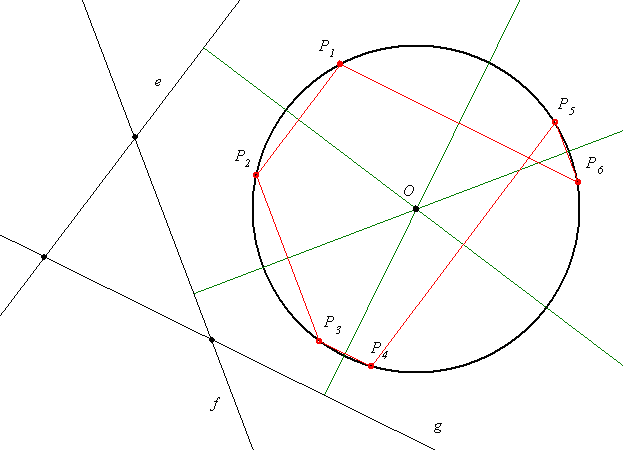
 Általánosítsuk Géza 206-os felszólalásban kitűzött példáját. Az általánosításnak két fokozatát látom, egyelőre csak az elsőt mondom el, hátha rájön valaki a további általánosításra.
Legyen adott a k kör és az A, B, C kollineáris pontok a síkon. Tekintsük a k kör tetszőleges P1 pontját, és k további Pk pontjait úgy, hogy P1P2 átmenjen A-n, P2P3 a B-n, P3P4 a C-n, P4P5 megint A-n, P5P6 a B-n, végül P6P7-t a C-n. Igazoljuk, hogy P7=P1.
|
|
|
| [208] BohnerGéza | 2005-02-28 22:24:20 |
 A [206]-ban szereplő feladat egy megoldása Hraskó Andrástól:
Az adott iránnyal párhuzamos húzás helyett alkalmazzunk tengelyes tükrözést, az irányra merőleges, a kör kp-ján átmenő egyenesre. Csak azt kell igazolni, hogy a t1 t2 t3 t1 t2 t3 kompozíció az identitás, ami nem nehéz.
/ Az első három és a második tükrözés szorzata is ugyanarra az egy tengelyre tükrözéssel helyettesíthető. /
|
| Előzmény: [206] BohnerGéza, 2005-02-21 23:55:14 |
|
| [207] lorantfy | 2005-02-27 16:19:32 |
 Kedves Géza!
Jó a feladat! Egyetlen gondom van vele, hogy nem én találtam ki :-)
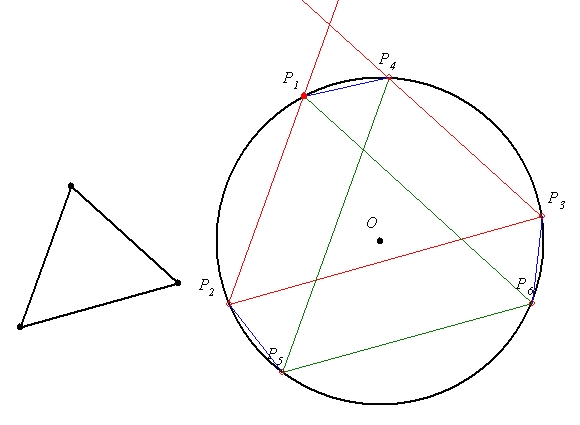
49. feladat megoldása: P4P5 párhuzamos P1P2, így P1P2P5P4 húrtrapéz, vagyis szárai egyenlőek. Hasonlóan húrtrapézok lesznek a P2P3P6P5 és P3P4P7P6 négyszögek. Száraik mind egyenlőek, tehát
P1P4=P7P4, vagyis P1=P7.
|
 |
| Előzmény: [206] BohnerGéza, 2005-02-21 23:55:14 |
|
| [206] BohnerGéza | 2005-02-21 23:55:14 |
 Adott három tetszőleges irány (egyenes ) és egy kör. Vegyünk föl a körön egy P1 pontot,a további P-k is a körön legyenek úgy, hogy P1 P2 párhuzamos az első iránnyal, P2 P3 a másodikkal, P3 P4 a harmadikkal, P4 P5 az elsővel, ... . Igazoljuk, hogy P1=P7!
|
|
| [205] BohnerGéza | 2005-02-18 15:02:17 |
 A síkbeli egybevágősági leképezések számítógépes megvalósítása legegyszerűen mátrixok segítségével oldható meg.
A forgatás mátrixa a következő, ahol alfa a forgatás szöge a (p,q) pont az origó képe, ez külön, egyszerűen számolható.
|
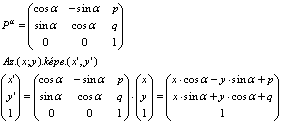 |
| Előzmény: [200] lorantfy, 2005-01-30 21:58:51 |
|
| [204] petrot | 2005-02-01 14:59:46 |
 Kedves fórumozók!
Fel szeretném hívni a figyelmeteket egy 3D szerkesztőprogramra, remélem tetszeni fog!
link: http://euler3d.uw.hu
Várom a véleményeteket (+,-), hozzászólásotokat!
Üdv! petrot
|
|
| [203] lorantfy | 2005-01-31 22:24:35 |
 Kedves 2501!
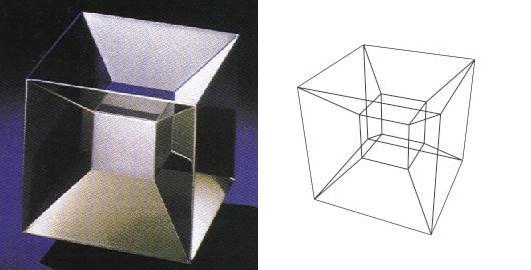
Kösz a segítséget és jó a példa is ami a témában a 48. feladat. Én még adós vagyok a 4D-s kocka 3D-s vetületével. A kockavázra feszülő szappanhártya-minimálfelületre hasonlít.
|
 |
| Előzmény: [202] 2501, 2005-01-31 10:54:54 |
|
|
|
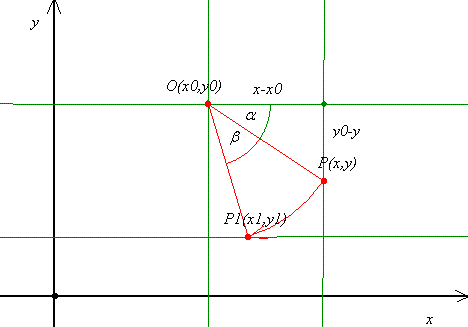
| [200] lorantfy | 2005-01-30 21:58:51 |
 Kedves Fórumosok!
"Zoleka"-tól kaptam a feladatot e-mail-ben. Programot ír és kellene Neki P pont elforgatása  szöggel adott O pont körül. szöggel adott O pont körül.
1. Kiszámolni  szöget: szöget: 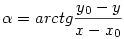
2. 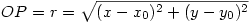
3. Az új koordináták:
x1=x0+rcos( + + ) )
y1=y0-rcos( + + ) )
Ha tudtok jobbat írjátok be, vagy bármi más geometriát, mert elhal a téma!
|
 |
|
| [198] lorantfy | 2004-11-28 17:10:22 |
 Kedves Károly!
Te mindig egy lépéssel előttem jársz. Gondoltam felteszi valaki az ábrát, aztán megbeszéljük hogyan öröklődnek felfelé a tulajdonságok. Te ezt már megtetted, köszönet!
|
| Előzmény: [197] Hajba Károly, 2004-11-28 00:29:26 |
|
| [197] Hajba Károly | 2004-11-28 00:29:26 |
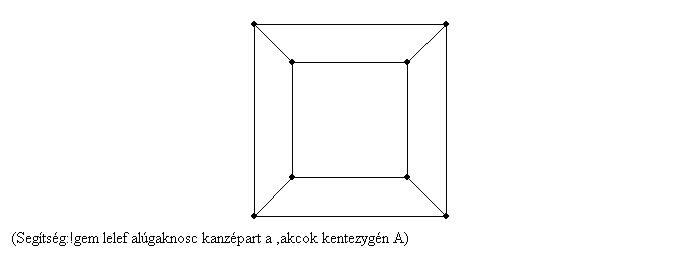
 47. feladathoz:
Vizsgáljuk meg, hogy egy adott dimenziónál hogyan alakítjuk ki a dimenzónagyságra jellemző egységnyi idomot. Mivel olyan magasabb dimenziójú idomról is beszélnünk kell, mire nincs szavunk, az alábbi egységes jelölésrendszert vezetem be. D - dimenzió mértéke, ID,d a D dimenzióbeli egységidom d dimenziójú egységidomelemének számossága. Értelemszerűen D d d 0. Így a pont jelőlése ID,0, egységszakasz ID,1, egységnégyzet ID,2, egységkocka ID,3, míg a keresett 4. dimenziójú egységidom ID,4. 0. Így a pont jelőlése ID,0, egységszakasz ID,1, egységnégyzet ID,2, egységkocka ID,3, míg a keresett 4. dimenziójú egységidom ID,4.
Az egységpont I0,0=1, egységszakasz I1,0=2, I1,1=1, azaz a kisebb dimenziójú egységidomot egységnyivel eltolom az új dimenzióiránnyal párhuzamosan. I0,0=1 megduplázódik I1,0=2 és bejön I1,1=1. Az egységnégyzet I2,0=4, I2,1=4, I2,2=1, itt már pontosan leírhatjuk az adott elem dimenzónövekedéssel járó elemszám növekedését. Azaz az eltolás miatt megduplázzuk és hozzájön az eggyel kisebb dimenziójú elemek száma, melyből az eltolással aktuális dimenziójú elem keletkezett. ID,d=2*ID-1,d+ID-1,d-1
Tehát a 4 dimenziójú egységidom részegységidomai a következők. Pont: I4,1=16, egységszakasz: I4,2=32, egységnégyzet: I4,2=24, egységkocka: I4,3=8, 4 dimenziós egységidom: I4,4=1. A 4 dimenziójú kocka síkbeli ábrája egy olyan gráf, melynek 16 pontja van, minden pontból 4 él indul ki, mely összesen 32 él és bármely pontból kiindulva 4+2n(n 0,N+) lépésszámmal lehet visszaérni. Továbbá a négyes hurkok négyzet vagy trapéz alakot adnak ki. 0,N+) lépésszámmal lehet visszaérni. Továbbá a négyes hurkok négyzet vagy trapéz alakot adnak ki.
HK
|
| Előzmény: [196] lorantfy, 2004-11-27 23:06:38 |
|
| [196] lorantfy | 2004-11-27 23:06:38 |
 47. feladat: Jelenítsük meg a láthatatlant! (lásd könyvajánló) Az ábrán egy 3 dimenziós kocka 2 dimenziós képe látható. Lépjünk egy dimenzióval feljebb!
Rajzoljuk meg egy 4 dimenziós "kocka" 3 dimenziós vetületének síkbeli ábráját!
Hány 3 dimenziós kocka határolja a 4 dimenziós testet?
|
 |
|
|
|
|
| [192] BohnerGéza | 2004-11-25 18:38:10 |
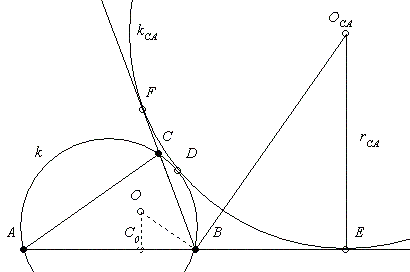
 A 45. feladat [182.] egy megoldása. A Fórum - Kürschák-verseny 5. hozzászólásában szerepel a Casey-tétel. Az alapkör a k körülírt kör, az érintőkörök: az A, B és C nullkörök, valamint a k-ca kör. Jelöljük a BF=BE szakaszt x-szel, ekkor AB*CF+BF*CA=AE*BC, azaz c(x-a)+xb=(c+x)a. Innen (b+c-a)x=2ca, 2(s-a)x=2ca, ( innen olvashatóbban a következő hozzászólásban! ) x=ca/(s-a). Tekintve, hogy a BEOca és az OCoB háromszögek hasonlók ( O a beírt kör sugara, így OCo=ró és CoB=s-b ) r-ca=ca(s-b)/ró(s-a).
A folytatás a jobb olvashatóság érdekében ( és lustaságom miatt ) a következő hozzászólásban lesz.
Megjegyzések:
1.A feladatot elkapkodva adtam föl, így szövegéből kimaradt, hogy a körülírt kört kívülről érintő körről van szó, valamint a három megadott sugár szorzata nem adható meg csak a körülírt kör sugara és a félkerület szorzatával.
2.A k-ac kör és a k-ca két különböző kör, ilyen jellegű - a körülírt kört kívülről érintő - kör 6 db van.
|
 |
| Előzmény: [182] BohnerGéza, 2004-11-17 09:35:09 |
|
|
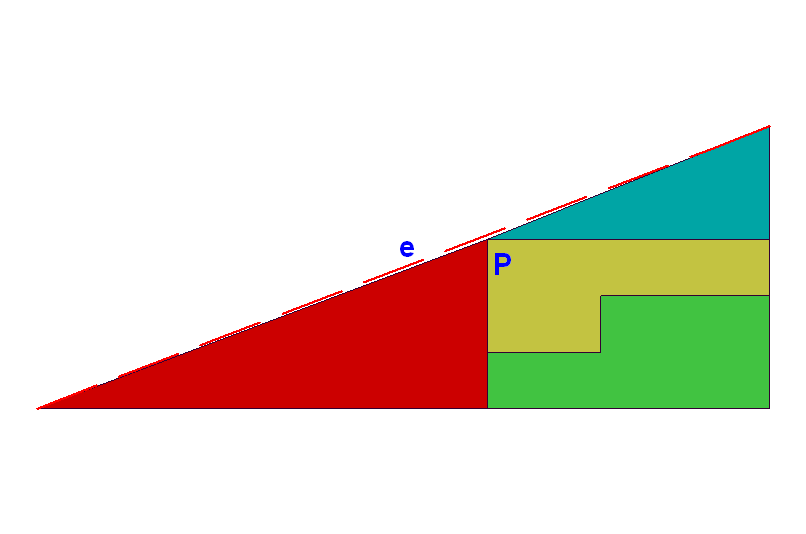
| [190] Hajba Károly | 2004-11-24 14:47:40 |
 Kedves Svejk!
Félrevezető a vastag keret. Átrajzoltam vékonnyal és behúztam az igazi átfogót.
Cserébe mondd meg nekünk, hogy mennyi a P töréspont és e átfogó közötti távolság, ha a háromszög két befogója 13 és 5 egység.
HK
|
 |
| Előzmény: [187] svejk, 2004-11-24 13:22:42 |
|
|
| [188] jenei.attila | 2004-11-24 13:23:21 |
 Az a baj, hogy a befoglaló "háromszög" nem háromszög, csak majdnem. Ugyanis ha az lenne, akkor a piros és a sötétzöld háromszögeknek hasonlóaknak kellene lenni, de nem azok (2/5 nem = 5/8).
|
| Előzmény: [186] svejk, 2004-11-24 13:15:02 |
|
| [187] svejk | 2004-11-24 13:22:42 |
 Kedves Matekosok!
Elnézést, hogy előbb a képet küldtem.:( Úgy tudom, hogy ez egy elég régi feladvány, de még senkitől nem kaptam kielégítő magyarázatot, hogy miért változnak meg a részterületek összegei. Help!
A választ előre is köszönöm!
|
|






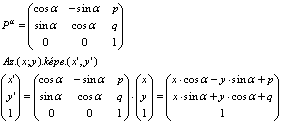



 -(Py-Oy)sin
-(Py-Oy)sin  szöget:
szöget: 

 d
d 0,N+) lépésszámmal lehet visszaérni. Továbbá a négyes hurkok négyzet vagy trapéz alakot adnak ki.
0,N+) lépésszámmal lehet visszaérni. Továbbá a négyes hurkok négyzet vagy trapéz alakot adnak ki. 

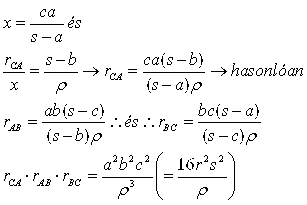

 csúcsait kössük össze a szemközti oldalak egyik harmadoló pontjával. Mekkora a keletkező DEF
csúcsait kössük össze a szemközti oldalak egyik harmadoló pontjával. Mekkora a keletkező DEF