| [40] Csimby | 2004-02-05 09:07:34 |
 Semelyik kettő ne legyen egybevágó!
|
|
| [39] lorantfy | 2004-02-05 08:33:06 |
 Kedves Csimbi!
A 12. feladathoz annyi lenne a kérdésem, hogy a 7 háromszög között nem lehetnek egybevágóak, vagy csak annyi a kikötés, hogy nem lehet mind egybevágó?
|
| Előzmény: [37] Csimby, 2004-02-04 19:59:04 |
|
| [38] Csillag | 2004-02-04 21:28:41 |
 Tisztelt Érdeklődők!
Nem Penrose foglalkozott először a sík nem periodikus csempézésével. Eredetileg 25000 körüli volt a sík nem periodikus lefedéséhez használt különböző csempék száma, majd 100. Ezt a számot Rafael Robinson 6-ra javította, és azon dolgozott, hogy minimális számú különböző csempével fedhesse le a síkot (nem periodikusan). Penrose ezután jött elő egy szintén 6 csempéből álló halmazzal, amit később leegyszerűsített 2 eleműre. Roger Penrose-ról pl. a következő könyvben olvashatunk: Staar Gyula: Matematikusok és teremtett világuk, Vince Kiadó
GB
|
| Előzmény: [36] Hajba Károly, 2004-02-04 10:38:02 |
|
| [37] Csimby | 2004-02-04 19:59:04 |
 12. Feladat
Osszunk fel egy négyzetet 7 db hasonló, de nem egybevágó háromszögre.
13. Feladat
Pakoljunk bele 7 db 1/2 oldalhosszúságú szabályos háromszöget egy egység oldalú négyzetbe, átfedések nélkül.
|
|
| [36] Hajba Károly | 2004-02-04 10:38:02 |
 Kedves Attila!
Igen Penrose jött ki előszőr ilyenekkel, elő kellene keresnem a régi KöMaL számokat, de talán az archívumba már fel van rakva a '70-es évek vége, abban foglalkoztak e témával.
A matematikai hátterében nem vagyok mélyen benne, csak autodidakta módon és szintem, de szakmám miatt folyamatosan "edzésben tartom" a térlátásomat, így a "parkettázás" a hobbimmá vált. Továbbá egy jó kis CAD rendszer a kezem alá dolgozik, tehát az elképzelt megoldásokat könnyen ki is próbálhatom. Az eredményeket magad is láthatod korábbi képeimnél.
HK
|
| Előzmény: [35] jenei.attila, 2004-02-04 10:13:38 |
|
| [35] jenei.attila | 2004-02-04 10:13:38 |
 Kedves Károly!
Nagyon szép a 4. feladatra adott megoldásod. A középponton átmenő körívekkel való felosztásig én is eljutottam, aztán valami olyasmire gondoltam, hogy bizonyos idomok egyes határvonalait kellene elhagyni, olyanokat amelyek a középpontot tartalmazzák. Így egyfajta félig nyílt alakzatok jöhettek volna létre, de tovább nem jutottam, meg amúgy sem lett volna az "igazi" megoldás.
A parkettázós témában úgy látom otthon vagy, a legutóbbi hozzászólásodban ha jól értem ún. aperiodikus parkettázást adtál meg. Úgy tudom először ilyet Roger Penrose adott meg, nem kis meglepetést okozva ezzel matematikus körökben. Az ő parkettázása ha jól emlékszek két különböző alakzatot használ. Ezzel kapcsolatban mit tudsz, vagy ha valamit rosszul értettem, kérlek javíts ki.
Üdvözlettel: Jenei Attila
|
| Előzmény: [30] Hajba Károly, 2004-02-03 13:06:53 |
|
| [34] Hajba Károly | 2004-02-04 00:58:26 |
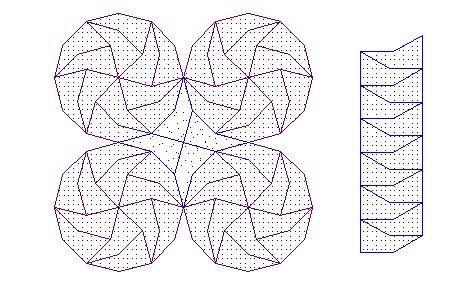
 Tovább gombolyítom e téma és idom fonalát: (1) Ha jól emlékszem ilyen idomokról volt kömalos feladat és cikk is anno az "én időmben". (2) Ezen idommal, ha jól sejtem, végtelenféleképpen lehet lefedni a síkot úgy, hogy a keletkezett minta nem transzformálható át önmagába. (3) Sok érdekes szólóminta is kialakítható belőle, például László említette Jin-Jang is:
|
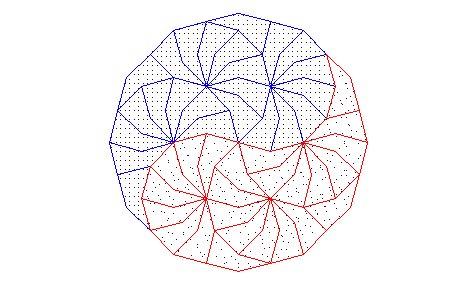 |
| Előzmény: [33] Hajba Károly, 2004-02-04 00:47:19 |
|
|
| [32] lorantfy | 2004-02-03 23:02:41 |
 Kedves Károly és Fórumosok!
A pajzs alakú darabnak két domború és egy homorú oldala van. Ha az egyik domború oldalt egyenes szakasszal helyettesítjük, akkor lefedhető a sík hézagmentesen. Nem tudom erre gondoltál-e vagy valamilyen más formát találtál ki? Mindenesetre én még nem láttam ilyen térburkolatot. Javasolhatnánk valamelyik gyártó cégnek!
(Csak két varit rajzoltam, mert az Euklides progival kicsit körülményes ezt szerkeszteni)
|
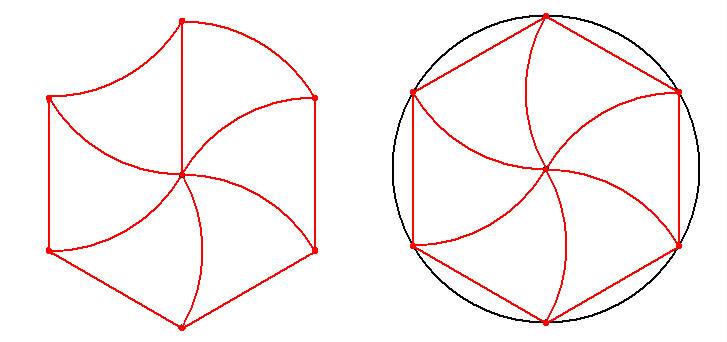 |
| Előzmény: [31] Hajba Károly, 2004-02-03 13:13:24 |
|
| [31] Hajba Károly | 2004-02-03 13:13:24 |
 11. feladat:
A 4. feladat megoldásának idomát kis módosítással át lehet-e alakítani úgy, hogy ennek és tükörképének felhasználásával a teret hiánytalanul le tudjuk fedni, akár többféle elrendezéssel is?
Hajba Károly
|
|
| [30] Hajba Károly | 2004-02-03 13:06:53 |
 Kedves Csillag!
Hozzászólásodra egy gimis OKTV-s emlékem ugrott be (a '70-es évek vége). Felettünk néhány évvel volt járatos egy történet, mely állítólag megtörtént: az egyik nagytudású versenyző, ki utazótáskányi feladatgyűjteménnyel ment a versenyre, az egyik feladat megoldását oly módon teljesítette, hogy megjelölte, mely feladatgyűjteményből való a pálda és hol található a megoldása.
Nos úgy gondolom, hogy ide sokan azért nézünk be, mert örömmel tölt el egy-egy probléma megoldásán való gondolkodás, s esetleg a megoldás saját erőből történő megtalálása. Továbbá attól, hogy valaki szereti a matekot, nem biztos, hogy minden témában egyformán vág az agya, de lehet, hogy csak jelenleg nincs rá ideje elmerülni benne.
Tehát szerintem ez nem az OKTV, így ha valaki ismeri egy feladat megoldását vagy tudja annak előfordulási helyét, nem illik azt lelőni, hátha valaki szeretne rajta gondolkodni, s senki sem akarja a spanyolviaszt feltalálni. Továbbá egy érdekes feladat aránylag gyors megoldásával és közzétételével, mint eme feladat is, nem illik mások örömét elvenni.
Íme az én megoldásom, több változat egy képbe sűrítve, melyet már korábban jeleztem:
|
 |
| Előzmény: [29] Csillag, 2004-02-02 20:05:04 |
|
| [29] Csillag | 2004-02-02 20:05:04 |
 Tisztelt Látogatók!
Elég régóta rágódnak itt egyesek a 4. feladat megoldásán, pedig a 2001/1-5 KöMaLok címlapján szereplő ábra pont ezt a feladatot oldja meg. (Az ott szereplő megoldás Salát Máté ötletéből készült) A következő két probléma is nagyon szép (projektív geometriai) tétel és érdemes őket ismerni, ha valaki versenyre megy. (A tételek megtalálhatóak Hajós György: Bevezetés a geometriába c. könyvében):
10. feladat: a) Bizonyítsá(to)k be Pascal tételét: egy közönséges kúpszeletbe írt hatszög átellenes oldalpárjai egymást egy egyenes három pontjában metszik. (A probléma már felmerült a Matek OKTV rovatban -> 17. hozzászólás, de ott nem szerepel bizonyítás)
b) Bizonyítsá(to)k be Brianchon tételét: egy közönséges kúpszelet köré írt hatszög átellenes oldalpárjait összekötő egyenesek egymást egy közös pontban metszik. (A 3 egyenes közös pontja a hatszög Brianchon-féle pontja.)
c) Hogyan tudná(to)k felhasználni a Papposz-Pascal tétel állítását az idei matek OKTV II. kat. I. ford. 5. feladatában? GB
|
|
| [28] lorantfy | 2004-02-01 22:37:09 |
 Kedves Csimbi, Károly és Fórumosok!
4. feladat megoldása: Először én is azt hittem, hogy átverés Csimbi ügyes kis feladata, már azon voltam, hogy bebizonyítom, ilyen felosztás nem létezik…
Aztán arra gondoltam, ha létezik ilyen alakzat, mármint az ilyen módon részekre felosztott kör, akkor biztos, hogy felhasználták már valami ismert ábrában, logóban vagy reklámban és láttam már valahol ezt a felosztást.
Annyi körívekből álló édekes ábra van (jing-jang). Aztán gyermekkori emlékek pörögtek a fejemben és már meg is volt a megoldás.
Ezek alapján és Károly segítségét felhasználva egy körzővel és egy vonalzóval (vagy szabadkézzel) bárki megrajzolhatja a felosztást.
(Ha valaki nagyon kíváncsi egy kis segítséget még feltettem egy másik témába.)
|
| Előzmény: [11] Hajba Károly, 2004-01-14 00:36:02 |
|
| [27] BohnerGéza | 2004-01-23 13:52:13 |
 A 2. feladat megérdemli, hogy foglalkozzunk vele, akkor is, ha már tripolár koordinátákkal általánosabban igazolták. A 4. hozzászólás ábrájának jelöléseit használva, de az 1, 2, 3-as indexeket a, b, c-re változtatva, ( még nem tanultam meg a TeX-tet, és így olvashatóbb ) kiegészíthető még a továbbiakkal:
Legyen K az ABC, K* az OaObOc háromszög körülírt körének középpontja, S az SaSbSc, S* pedig OaObOc háromszög súlypontja ( ha léteznek ). Ekkor az Euler-egyenesek metszéspontján átmegy még a KK* és SS* egyenes is, valamint PK párhuzamos K*S*-gal.
Elemi bizonyítást egyelőre nem ismerek. Talán ezek az észrevételek segítenek a kitalálásában.
|
|
| [26] lorantfy | 2004-01-21 22:09:30 |
 Kedves Gubbubu!
Persze csak vázoltam egy megoldást mert nagy rohanásban voltam, mint mindig.
2. ponthoz annyit, hogy ha a szög 90o akkor nyilván nagyobb egy hegyesszögnél, ha tovább növeljük a szöget a B metszéspont a másik oldalon keletkezik.
|
| Előzmény: [25] Gubbubu, 2004-01-21 20:29:33 |
|
| [25] Gubbubu | 2004-01-21 20:29:33 |
 Kedves László!
Köszönöm a megoldást! Néhány pontosítás vagy kiegészítés:
0. Azt, hogy A1 a CDB belsejébe esik, azt hiszem, C középpontú koncentrikus körök segítségével egyszerűen be lehet látni (kérdés persze, hogy milyen mélységig "fejtsünk vissza" egy elemi tételt az axiómákig, és mit fogadjunk el "szemléletesen igaz"nak, illetve ebből mit írjunk le egy korlátozott hosszúságú fórumos szövegben, ezek mindig problémák, amiken mindig sokat szoktam filózni);
1. "ebből már következik" hogy a kérdéses szög kisebb: azt hiszem, hogy ezt nem egetrengetően nehéz belátni (szemléletesen elég világos), de azért nem is olyan könnyű.
Mindenesetre visszavezettük a térbeli szituációt a síkgeometriára, és lényegében ez volt a célom.
2. A bizonyítás csak azon D-n átmenő egyenesekre működik, melyek metszik AB-t. A többi D-n átmenő egyenes nem jöhet szóba, mert szögük CD-vel 90o vagy nagyobb (ezt is be lehet látni egy-két szóban).
Még egy megjegyzés: a középiskolai tankönyvek többsége ebből a tételből egészen egyszerűen definíciót csinál ("nevezzük egyenes és sík szögét az egyenes és síkba eső merőleges vetülete szögének"), pedig ez igazából egy tétel, ez motivált a kitűzésben.
Létezik a feladatnak általánosítása is, mégpedig n-dimenziós euklideszi terekre. Ha valakinek van kedve, gondolkodjon el, hogy mi ez az általánosítás, és hogyan lehet belátni (ha sikerül elegendő pontossággal megfogalmaznom, kitúzöm a "nehezebbek" topikban, de addig is lehet gondolkodni).
Üdv: G.
|
| Előzmény: [24] lorantfy, 2004-01-21 14:28:29 |
|
|
| [23] Gubbubu | 2004-01-20 18:47:02 |
 Még néhány feladat,
a lineáris választékbővítés jegyében:
. .
7. feladat: Igaz-e, hogy a (nem elfajuló) háromszög beírt köre a legnagyobb sugarú kör, melyet a háromszöglemez tartalmaz?
8. feladat: Igaz-e, hogy a (nem elfajuló) háromszög köré írt kör a legkisebb sugarú kör, mely tartalmazza a háromszöglemezt?
9. feladat: Igazoljuk, hogy egy síkot egy pontban metsző ("döfő") egyenes a metszésponton átmenő, síkbeli egyenesek közül épp saját merőleges vetületével zár be minimális szöget
(tkp. ha minden síkbeli, a döfésponton átmenő egyenes esetében megmérjük a döfő egyenessel bezárt szögét, akkor az így kapott szögmértékek halmazában van legkisebb elem, és ez épp az a szög, amelyet a döfő egyenes a merőleges vetületével zár be).
|
|
| [22] Gubbubu | 2004-01-19 12:07:31 |
 Kedves Onogur!
Nagyon köszönöm a megoldást. Egyébként a kérdéses szög a szénatom "tetraéder alakúnak képzelt elektronszerkezetének" (a kifejezés elég pongyola, ezért van idézőjelben, nem azért, mert idézet egy tankönyvből) az egyik alapadata. Ilyennek képzeljük a kötésszöget pl. a metánmolekula vagy a gyémánt-atomrács két kovalens kötése között.
A kérdéses szög szokásos (közelítő) értéke a szerves kémia tankönyvekben és jegyzetekben 109,5o szokott lenni.
A feladat a gyakorlati jellegű, alkalmazott matematikai feladatok egy igen kézenfekvő példája, talán ezért nem találkoztam vele soha matematikaórán.
Üdv:G.
|
| Előzmény: [20] Hajba Károly, 2004-01-17 00:40:03 |
|
|
| [20] Hajba Károly | 2004-01-17 00:40:03 |
 Kedves gubbubu!
Bevallom őszintén nem ismerem a vegyészek "alapszögét", de mint érdekes feladvány, elgondolkoztam rajta. Tehát
Megoldás az 5. feladatra:
A szabályos tetraéder köré írható kör sugara 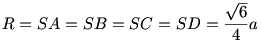 .(Lásd 4-jegyű függvénytábla :o) Így az .(Lásd 4-jegyű függvénytábla :o) Így az  szög cosinustétel segítségével megadható. szög cosinustétel segítségével megadható.
12=R2+R2-2*R*R*cos( ) )
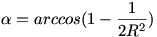
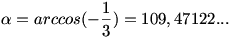
HK
|
| Előzmény: [16] Gubbubu, 2004-01-16 00:16:01 |
|
| [19] lorantfy | 2004-01-16 14:45:13 |
 Kedves Géza!
Ha jól látom ez az általánositás pontosan megegyezik az enyémmel, csak más megfogalmazásban!
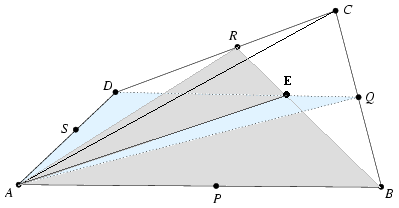
Mivel a négy pont nincs egy síkban a BD és AC szakaszokat behúzva tetraédert kapunk.
Az ABR, BCS, CDP és DAQ síkok metszésvonalai páronkánt az AE, BF, CG és DH egyeneseket adják, és ezek metszéspontja az M pont. (Fel kell venni még ACT és BDV síkokat, de ezek egyértelműen adódnak.)
A tétel teljesen formálisan átírható térbelivé persze a tetraéder élein lévő P,Q,R,S,T,V pontok segítségével.
|
 |
| Előzmény: [18] Kós Géza, 2004-01-16 10:21:08 |
|
| [18] Kós Géza | 2004-01-16 10:21:08 |
 Én egy másik irányban keresném a térbeli általánosítást... Az, hogy négy, ráadásul térbeli egyenes egy ponton megy át, nagyon erős követelmény.
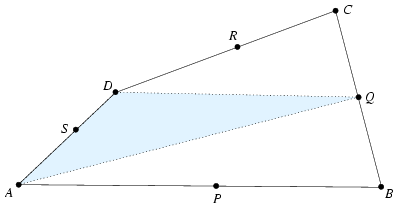
Legyen A,B,C,D négy olyan pont a térben, amik nincsenek egy síkban. Az AB, BC, CD, DA egyeneseken kiválasztjuk a P, A, R, S pontokat. Vizsgáljuk meg, hogy az ABR, BCS, CDP és DAQ síkok mikor mennek át egy ponton.
A Menelaosz-tétel térbeli változata pedig azt kérdezheti, hogy a P,Q,R,S pontok mikor vannak egy síkban.
* * *
(A \cdot paranccsal lehet középre pontot, azaz szorzásjelet tenni.)
|
 |
| Előzmény: [17] lorantfy, 2004-01-16 09:28:41 |
|
| [17] lorantfy | 2004-01-16 09:28:41 |
 Kedves Tamás és Fórumosok!
Tényleg nagyon szép bizonyítások találhatók a honlapon amit megadtál. Érdemes megnézni!
Ceva tétele:
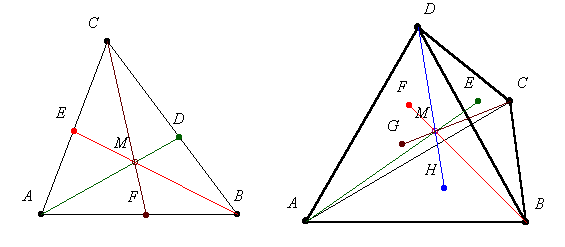
Az ABC háromszögben AD, BE és CF egyenesek akkor és csak akkor metszik egymást egy pontban (M) ha
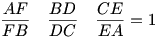
6.feladat: Fogalmazzuk meg a tétel térbeli általánosítását!
E,F,G,H pontok az ABCD tetraéder oldallapjain vannak. (Ceva tétel alkalmazása 6.b feladat megoldásában: "Versenyfeladatok" [26]nadorp hozzászólásban!)
|
 |
| Előzmény: [14] tarcsay, 2004-01-15 15:44:55 |
|
| [16] Gubbubu | 2004-01-16 00:16:01 |
 Egy - tulajdonképp klasszikus, de nagyon hanyagolt - feladat:
5. feladat:
Adott az ABCD szabályos (mondjuk egységnyi oldalú) tetraéder. Legyen S e tetraéder "középpontja" (szabatosabban: súlypontja). Számoljuk ki az a= ASB= ASB= CSB szöget! CSB szöget!
De pontos értéket kérek, például egy törtszám szinuszát vagy gyökkifejezést, ne közelítőt (azt a vegyész-matematikusok vsz. kívülről fújják...)!
|
 |
|








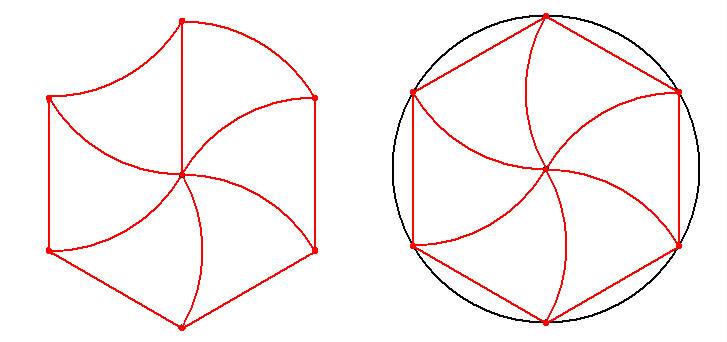



 <BDC
<BDC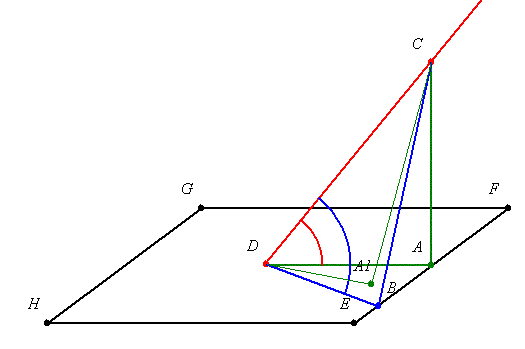
 szög cosinustétel segítségével megadható.
szög cosinustétel segítségével megadható. 



