|
|
|
| [518] Cckek | 2006-10-18 20:19:07 |
 Legyen M az ABC háromszög AB oldalának egy A-tol és B-től különböző pontja.Az CMB háromszög köré írt kör az AC oldalt másodszor N-ben metszi.Legyen O az AMN háromszög köré írt kör középpontja. Bizonyítsuk be, hogy AO merőleges BC-re. Elkelne a segítség. Köszi.
|
|
| [517] Hajba Károly | 2006-10-15 16:58:11 |
 Szerintem nem. Azt kell belátni, hogy legalább két olyan oldala van, hogy a tömegközéppontjának merőleges vetülete beleesik az oldallapba (v. az élére).
(Persze nem vizsgáltam, hogy a két feltétel között milyen összefüggés adódik.)
|
| Előzmény: [516] Cckek, 2006-10-15 15:59:43 |
|
|
|
|
|
| [512] jonas | 2006-10-15 11:26:53 |
 Ezt a feladatot talán ismeritek.
Igaz-e, hogy minden tetraédernek legalább két oldala van, amin megáll (ha lerakjuk vízszintes terepre)?
|
|
|
|
| [509] nadorp | 2006-10-13 19:51:58 |
 Valamit félreérthetsz. A feladat szerint az 1), 2) és és 3) feltételnek teljesülnie kell. Akkor miért teszed fel, hogy ezek közül kettő nem teljesül ?
|
| Előzmény: [508] Iván88, 2006-10-13 18:37:37 |
|
|
| [507] kdano | 2006-10-12 20:19:13 |
 Tény, hogy a párhuzamos egyeneseket meghatározó pontok egy síkban vannak, de ebből én nem látom az ellentmondást... Szerintem te az első feltételt akartad megdönteni, de hát attól még, hogy bizonyos pontnégyesek egy síkban vannak, nem feltétlenül van minden pont egy síkban.
(érvelésedre egyébként lejjebb találsz ellenpéldát...)
|
| Előzmény: [506] Iván88, 2006-10-12 20:06:02 |
|
| [506] Iván88 | 2006-10-12 20:06:02 |
 Ha AB és CD szakasz (s így azegyenes) párhuzamos, akkor nem kitérőek, és nem metszik egymást, ezért az ABCD négyszög egy síkidom, sőt egy trapéz, tehát ilyen "pontrendszer" nem létezik.
|
| Előzmény: [502] nadorp, 2006-10-11 20:46:45 |
|
| [505] kdano | 2006-10-12 18:13:00 |
 Talán a legegyszerűbb/legelegánsabb megoldás az, ha veszel egy szabályos 1004-szöget, majd két szemközti csúcsánál fogva 90 fokkal kiforgatod a térbe, s ehhez hozzáveszed az eredetit.
|
| Előzmény: [502] nadorp, 2006-10-11 20:46:45 |
|
|
| [503] Yegreg | 2006-10-11 22:21:05 |
 Ez idei Kürschák-példa volt:) azt hiszem, ilyesmi jó: egy gömb egy főkörén egy szabályos 2002-szög, valamint ezen 2002-szög két szemközti csúcsára illeszkedő, a korábbi főkörre merőleges főkörön egy szabályos hatszög (mármint, hogy 2 szemközti csúcsa egybeessen a 2002-szög szemközti csúcsaival).
|
|
| [502] nadorp | 2006-10-11 20:46:45 |
 Sziasztok !
Van egy példám, amivel nem boldogulok. Állítólag versenypélda, de sehol sem találom.
Megadható-e a 3-dimenziós térben 2006 pont a következő tulajdonságokkal:
1) a pontok nincsenek egy síkban
2) semelyik 3 nincs egy egyenesen
3) bármely A,B ponthoz létezik olyan C,D pont, hogy az AB szakasz párhuzamos a CD szakasszal
|
|
|
|
| [499] Porter | 2006-10-09 11:06:47 |
 Sirpi. Elkészült az a kis feet a progidhoz, ami megmondja, h milyen tipusú négyzetből mennyit használ fel?
|
|
| [498] Hajba Károly | 2006-10-07 23:34:49 |
 Kicsit visszatérnék a négyzetredarabolás problémájához, pontosabban ehhez kapcsolódóan egy hasonló problémához. Régebb óta foglalkoztat egy hasonló probléma. Adott (itt most) egy négyzet és ezt kell valahány kisebb négyzetre felosztani. Én a 11 részre osztás változatba merültem el, többszöri nekifutással.
Mit gondoltok, hányféle különböző (egymásba nem forgatható vagy tükrözhető) módon lehet egy négyzetet 11 kisebb négyzetre osztani? Először kiváncsi vagyok a megérzésetekre. Utána, ha nem bonyolult, valaki írhatna rá egy rutint, mert kiváncsi lennék a pontos eredményre is.
|
|
| [497] Csimby | 2006-10-03 21:18:10 |
 Ez egy maximális összsúlyú út keresése egy irányított körmentes gráfban. Ugyanis feleltessünk meg minden kockát egy-egy csúcsnak. Tekintsük ezt az n csúcsot abban a sorrendben ahogy a nekik megfelelő kockák az asztalon vannak (a1,a2,...,an). Ha i<j és aj kocka könnyebb, valamint keskenyebb mint ai kocka, akkor mutasson él ai-ből aj-be. Súlyozzunk minden aiaj élet 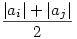 -vel, ahol |ai| = ai szélessége (ami megegyezik a magasságával). Vegyünk fel továbbá egy s ill. t csúcsot, s-et első, t-t utolsó csúcsnak. És mutasson él s-ből minden ai-be, ezek legyenek súlyozva -vel, ahol |ai| = ai szélessége (ami megegyezik a magasságával). Vegyünk fel továbbá egy s ill. t csúcsot, s-et első, t-t utolsó csúcsnak. És mutasson él s-ből minden ai-be, ezek legyenek súlyozva 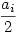 -vel. Illetve minden ai-ből mutasson él t-be szintén -vel. Illetve minden ai-ből mutasson él t-be szintén 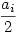 súlyozással. A csúcsok jelenlegi helyzete egy topológikus sorrend (csak előre megy él), ebben a következőképpen kereshetjük meg a leghosszabb utat (s:=a0, t:=an+1): Az ai pontra ha nincs ai-be futó él, akkor címkéje legyen 0, egyébként Pi azon pontok halmaza ahonnan van él ai-be. Az ai pont címkéje = súlyozással. A csúcsok jelenlegi helyzete egy topológikus sorrend (csak előre megy él), ebben a következőképpen kereshetjük meg a leghosszabb utat (s:=a0, t:=an+1): Az ai pontra ha nincs ai-be futó él, akkor címkéje legyen 0, egyébként Pi azon pontok halmaza ahonnan van él ai-be. Az ai pont címkéje = 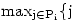 címkéje +cji}, ahol cji az aiaj él súlya. címkéje +cji}, ahol cji az aiaj él súlya.
|
| Előzmény: [479] Sanyi, 2006-10-03 11:09:11 |
|



 =90o-MAP
=90o-MAP





