|
|
| [544] BohnerGéza | 2006-11-13 22:15:45 |
 Az [533]-ban lévő feladatra:
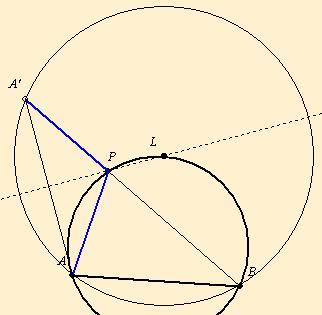
Az [537]-ben jenei.attila írt vázlatosan erről: A nem kisebbik ív nyilvánvaló. A két oldal összeadásához tükrözzük A-t az APB= gamma szög külső szögfelezőjére: A'. Ekkor BA' a keresett összeg. BA'A= gamma/2. A' az AB gamma/2 látókörén van, ennek középpontja L. BA' a leghosszabb, ha átmérője a látókörnek, azaz P=L.
|
 |
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
| [543] The Student | 2006-11-13 20:48:32 |
 Srácok fogy az idő (és lányok) valamit nem segítenétek, emrt én ehhez nem vagyok elég... Előre is köszi!
|
|
| [542] fermel | 2006-11-13 20:38:09 |
 Csimby és Attila! Nagyon köszönöm a segítségeteket.
Attila! Azt,hogy B' is rajta van azon a bizonyos körön, hogyan láttad be? Én szögekkel próbálkoztam, de még nem jött ki. Lehet, hogy túlbonyolítom? Segítenél? Köszönöm.
fermel
|
|
| [541] The Student | 2006-11-13 20:29:40 |
 Látom, ez is egy használható tanács volt! Köszi
|
|
|
|
| [538] The Student | 2006-11-13 18:49:08 |
 Sziasztok, új vagyok itt, de remélem sikerül érdekes témákat hoznom, illetve segítenem, bár eléggé tudtalan vagyok! Tudna nekem valaki segíteni, hogy hogy lehet megszerkeszteni csak körzővel egy négyzetet? Ha igen, akkor kérlek gyorsan írjatok, mert kell a házimba :) Köszi!
|
|
| [537] jenei.attila | 2006-11-13 11:12:11 |
 Ha jól emlékszek, ez nem rég kömal feladat volt. Vegyük a PA PB közül a hosszabbikat (pl. PA-t), ezt P felé meghosszabítva B'-t vegyük fel úgy, hogy PB'=PB legyen. Ekkor PA+PB=AB'. F legyen a z hosszabbik AB ív felezőpontja. Könnyű bizonyítani, hogy az F középpontú körön, amely átmegy A-n és B-n, rajta van B' is. Ezért a kérdéses összeg akkor maximális, ha AB' átmérője az F középpontú körnek.
|
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
|
| [535] Csimby | 2006-11-13 02:44:16 |
 Te jó ég ennyi hülyeséget mint amit az előbb írtam... Szóval, a Cosinus-tételben + helyett - van. És kell még az is, hogy ab akkor a legnagyobb, ha a=b, ez abból jön ki, hogy PAB területe = 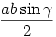 ahol ahol  állandó és a terület egyenlőszárú háromszögre a legnagyobb(hiszen állandó és a terület egyenlőszárú háromszögre a legnagyobb(hiszen 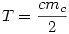 ahol c állandó és mc nyilván egyenlőszárúra a legnagyobb), vagyis amikor a=b. Tehát 2(a+b)2 ahol c állandó és mc nyilván egyenlőszárúra a legnagyobb), vagyis amikor a=b. Tehát 2(a+b)2 a2+b2=c2+2abcos a2+b2=c2+2abcos  . Ahol a jobb oldal a=b-nél a legnagyobb és ekkor egyenlőség áll fenn, tehát a bal oldal is ekkor veszi fel a maximumát, vagyis a+b is. Nem írok több bizonyítást fél3-kor, elnézést... remélem azért így is érthető és most már jó is. . Ahol a jobb oldal a=b-nél a legnagyobb és ekkor egyenlőség áll fenn, tehát a bal oldal is ekkor veszi fel a maximumát, vagyis a+b is. Nem írok több bizonyítást fél3-kor, elnézést... remélem azért így is érthető és most már jó is.
|
| Előzmény: [534] Csimby, 2006-11-13 02:29:23 |
|
|
| [533] fermel | 2006-11-12 22:59:26 |
 Szervusztok fiatalok! Szerintem jónéhányan már a gyerekeim lehetnétek (a legnagyobb fiam 20 éves), de most szükségem lenne a segítségetekre. Egy apró segédtételre kellene nekem 3 bizonyítás. Egyet már sikerült összehoznom az a:sinalfa=b:sinbéta=c:singamma=2R (elnézést a kezdetleges írásmódért)felhasználásával,de többet csak nem akaródzik kitalálnom. A feladat a következő: Adott egy kör és benne egy AB húr. Mozgassunk egy P pontot a körvonalon. Bizonyítsuk be, hogy a PA+PB akkor maximális, ha P az AB húr által meghatározott két körvonal közül a nagyobbik(pontosabban a nem kisebbik) felezőpontjában van!(azaz az AB húr felezőmerőlegese és a "nagyobbik" körvonal metszéspontja) Köszönöm a segítséget! fermel
|
|
|
|
|
| [529] BohnerGéza | 2006-11-10 19:23:02 |
 Calyd [523] kérdésére: 2*2-es mátrixszal a síknak csak az origót helybenhagyó, egyenestartó leképezései adhatóak meg, míg a 3*3-as adott formájú mátrixszal pl. az eltolások, bármely pont körüli forgatás, tetszőleges tengelyre tükrözés, stb is.
A tetszőleges 3*3-as mátrix a tér origót helybenhagyó, síktartó leképesei leírására alkalmas. Ha ezt leszűkítjük úgy, hogy a z = 1 sík potjainak képe maradjanak a síkon, kapjuk a fenti speciális esetet.
|
| Előzmény: [523] Calyd, 2006-11-09 17:37:28 |
|
| [528] Calyd | 2006-11-10 05:58:54 |
 Lóczi Lajosnak köszönöm szépen. Azóta persze megtalálta magam is, de itt is találtam hasznos információkat. ;)
|
|
|
|
| [525] defog | 2006-11-09 20:08:26 |
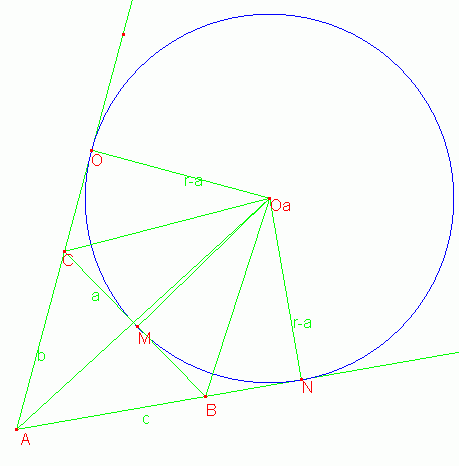
 Sziasztok! Az a helyzet, h kéne igazolnom 1 tételt, de nem találom seholse a bizonyítását. Ha valaki tudja, h kell bizonyítani azt, h a háromszög hozzáírható körének a sugara milyen kapcsolatban van a háromszög területével az segítsen pls. Előre is köszi!
|
|
|
| [523] Calyd | 2006-11-09 17:37:28 |
 Sziasztok!
Lehet, hogy a kérdés jobban illene valamilyen algebráról vagy programozásról szóló témába, de Bohner Gézának volt még itt anno egy hozzászólása, amelyben leírta egy alfa szögő forgatás mátrixát. Nekem erre lenne szükségem, csak éppenséggel térben. Szóval három dimenzióban hogy néz ki a forgatás? Nem tudom magamnak megfogalmazni, hogy mibe viszi a hagyományos egységvektorainkat egy forgatás térben. Továbbá az említett korábbi hozzászólásban "+1 dimenzió" van az origónak. Ez miért szükséges?
[ui: szerettem volna linket tenni a hozzaszolashoz, de a rendszer nem engedi]
|
|
|








 állandó és a terület egyenlőszárú háromszögre a legnagyobb(hiszen
állandó és a terület egyenlőszárú háromszögre a legnagyobb(hiszen  a2+b2=c2+2abcos
a2+b2=c2+2abcos