|
| [566] jonas | 2006-11-17 17:56:10 |
 Rendben, mutatom hogy szerkesztek négyzetet egy körzővel. Valószínűleg ennél sokkal egyszerűbb módszer is van, de ez jutott eszembe elsőként.
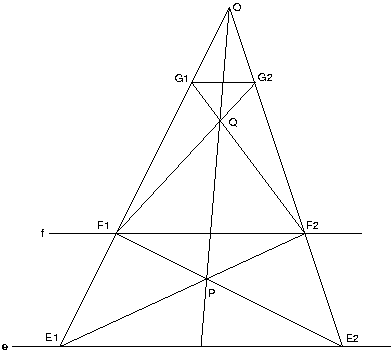
Először is elmondom, hogy lehet csak vonalzóval két adott párhuzamos egyeneshez egy harmadik párhuzamos egyenest szerkeszteni adott ponton át. Ez a Desargues-tételen alapul. Legyen e és f a két párhuzamos egyenes, és G1 az adott pont. Vegyünk fel egy tetszőleges O pontot. Legyen az OG1 egyenes metszéspontja e-vel illetve f-fel E1 illetve F1. Egy másik, az O-n átmenő tetszőleges egyenes az e és f egyenest az E2 és F2 pontban metszi. Legyen E1F2 és E2F1 metszete P. A G1F2 és az OP metszete legyen Q. Ez után az F1Q és az OF2E2 egyenesek metszete legyen G2. Végül G1G2 lesz a keresett g párhuzamos egyenes. (Én matematikus vagyok, ezért ezt a szerkesztést csak elméletben tudom elvégezni, valódi vonalzóval nagyon pontatlan lesz, de mivel te mérnök vagy, talán el tudod helyezni úgy a pontokat, hogy ne legyen túl nagy eltérés.)
Ha már ezt tudjuk, akkor a négyzet sem okozhat nehézséget. Ugyanis legyen k egy K középpontú kör. Ha most AB a kör egy húrja, akkor összekötve őket K-val az átmérők másik végpontjai C és D, így kapunk egy ABCD téglalapot. Ezután a téglalap párhuzamos oldalegyenesihez szerkeszthetünk K-n át párhuzamost, így kapunk két merőleges átmérőt, amiknek a végpontjai egy négyzetet határoznak meg.
|
| Előzmény: [565] Hajba Károly, 2006-11-17 08:51:12 |
|
|
| [564] josie | 2006-11-16 13:31:42 |
 szabályos testekről és a gúláról kénne minden!!!
|
|
|
| [562] S.Ákos | 2006-11-15 18:47:30 |
 Egy kissé egyszerűbb kérdés: mennyi a minimális körzőhasználatok száma, ha vonalzót is használhatunk?
|
|
|
| [560] AzO | 2006-11-14 22:54:59 |
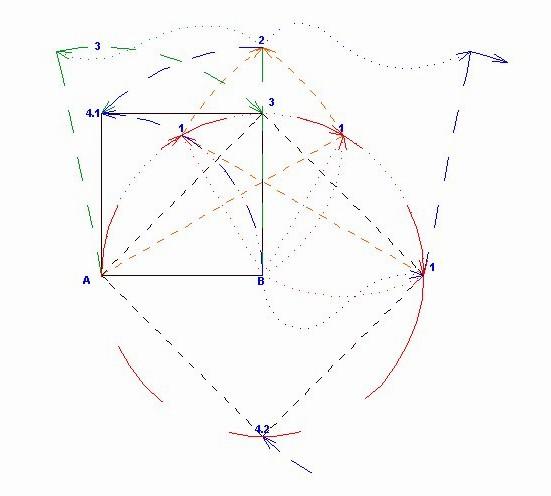
 Tenyleg ne aruld el hetfoig!!! Csak korzo hasznalata engedelyezett. Egy lepes addig tart, amig fel nem emeled a korzot. 2 pont adott a sikon, es kell 4 metszespont, ami negyzetet alkot. Legfeljebb 8 lepeses megoldas eseten +1 jegy a vizsgan.
|
| Előzmény: [556] Hajba Károly, 2006-11-14 20:55:26 |
|
|
|
|
| [556] Hajba Károly | 2006-11-14 20:55:26 |
 Nem mondok több infót, csak kérdezek. :o)
A feladat szerint egy üres papírra kell köríveket rajzolni úgy, hogy 4 darab metszéspont épp egy négyzetet adjon ki? és ehhez legfeljebb 8 körív rajzolható? A köríven egy tetszőleges pont bejelőlése az lépés?
Vagy adott két pont és erre kell négyzetet szerkeszteni?
|
| Előzmény: [552] Csimby, 2006-11-14 18:38:13 |
|
|
|
| [553] The Student | 2006-11-14 18:45:19 |
 Így lesz, remélem! Itt szerintem amúgy sem a feladatról van szó, hanem a 8 lépésről nem? Nekem csak az a lényeg, hogy a feladat menjen! És azt sem tudod még megszerkeszteni? Vagy csak a 8 lépéses dolog nem megy neked?
|
|
| [552] Csimby | 2006-11-14 18:38:13 |
 Pont azt kértem, hogy több infót itt NE közöljetek mert az egész évfolyam körzővel mászkál az egyetemen annyira lázba hozott mindenkit a téma és nem lenne jó ha itt lelőné valaki a poént amit egyenlőre még én sem tudok :-) Szóval Studenttel beszéljétek meg e-mailben...
|
| Előzmény: [549] Hajba Károly, 2006-11-14 08:30:05 |
|
| [551] The Student | 2006-11-14 16:43:44 |
 A megoldásodhoz fűznél egy kis magyarázatot, mert azért 10.es létemre nem annyira értem :)
|
|
| [550] The Student | 2006-11-14 16:24:19 |
 Köszi, aki segített, majd kibogarászom! És a Batthyány Kázmér gimibe :D csak nekünk ilyen jófej példákat kellene megoldani 10.-ben :D Hát nem vicces, de kapok érte ötöst... Üdv: Én
|
|
|
| [548] Csimby | 2006-11-14 01:43:26 |
 Ja és légyszi több infót ne közöljetek erről a példáról ugyanis ma adták fel az ELTE matematikus szakán és aki jövő hétig 8 lépésből megoldja +1 jegyet kap a geometria vizsgán.
|
| Előzmény: [547] Csimby, 2006-11-14 01:28:57 |
|
|
|
|
| [544] BohnerGéza | 2006-11-13 22:15:45 |
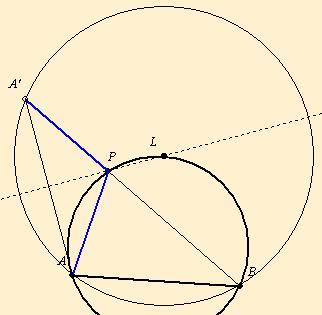
 Az [533]-ban lévő feladatra:
Az [537]-ben jenei.attila írt vázlatosan erről: A nem kisebbik ív nyilvánvaló. A két oldal összeadásához tükrözzük A-t az APB= gamma szög külső szögfelezőjére: A'. Ekkor BA' a keresett összeg. BA'A= gamma/2. A' az AB gamma/2 látókörén van, ennek középpontja L. BA' a leghosszabb, ha átmérője a látókörnek, azaz P=L.
|
 |
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
| [543] The Student | 2006-11-13 20:48:32 |
 Srácok fogy az idő (és lányok) valamit nem segítenétek, emrt én ehhez nem vagyok elég... Előre is köszi!
|
|