| [671] BohnerGéza | 2007-03-13 17:26:12 |
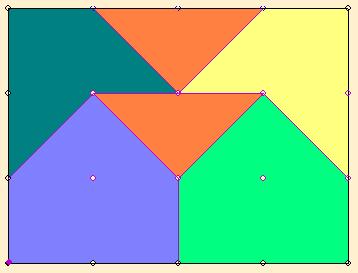
 Talán megtévesztő az ábra, de csak öt szín van, tehát öt tartomány. Mivel a téglalap oldalát nem vesszük a tartományhoz, egy tartomány két pontja közt a távolság kisebb mint gyök öt.
|
| Előzmény: [669] fermel, 2007-03-13 13:10:45 |
|
| [670] csocsi | 2007-03-13 16:42:54 |
 Sziasztok! Nekem lenne egy trigonometriához kapcsolódó kérdésem. A kérdés a következő: hogy próbálták elnevezni a nyelvújítás során a szinuszfüggvényt? Ezt a kérdést órán kaptuk, és már égen földön kerestem, de még egy névhez sem tudtam kötni a kérdést sajnos. Remélem tudtok segíteni!
|
|
| [669] fermel | 2007-03-13 13:10:45 |
 Esetleg leírnád bővebben a gondolatmenetedet? Odáig rendben van, hogy az általad írtból következik az eredeti feladat megoldása,de sajnos nekem nem áll össze, hogy miért igaz, amit leírtál. Köszönöm fermel
|
| Előzmény: [662] BohnerGéza, 2007-03-05 18:01:50 |
|
| [668] Andras17 | 2007-03-09 15:48:35 |
 Kellene egy kis segítség. 2 lapot kaptam de van 4 geometriai feladat az egyiken (A geometria sajnos nem az erősségem). Itt van a feladatlap(az 1; 4; 5; 7 kellene):
http://img80.imageshack.us/img80/3689/matek0gd7.jpg
Bármilyen segítséget szivessen fogadok, mert van még egy hasonló lapom csak az meg egyenletekkel meg más feladatokkal van tele.
|
|
| [667] sakkmath | 2007-03-07 11:09:37 |
 A következő, nehéznek tűnő - még megoldatlan - feladatot én találtam ki. Minden idevágó észrevétel, ötlet, vélemény érdekelne akkor is, ha az nem párosul részleges, vagy teljes megoldással.
|
 |
|
|
|
| [664] Doom | 2007-03-05 20:23:21 |
 Mekkora a görbületi sugara egy R sugarú hengerpaláston egyenletesen ( szöggel) emelkedő csavarvonalnak? szöggel) emelkedő csavarvonalnak?
|
|
| [663] Cckek | 2007-03-05 18:25:58 |
 Helló. A következő érdekes problémákkal találkoztam a hétvégén:
1. Határozzuk meg az ABC háromszög azon belső pontját melynek a háromszög csúcsaitól mért távolságainak a szorzata maximális/minimális.
2. Határozzuk meg az ABC háromszög azon belső pontját melynek a háromszög oldalaitól mért távolságainak a szorzata maximális/minimális.
|
|
| [662] BohnerGéza | 2007-03-05 18:01:50 |
 Ha az ábrán az egy színnel jelölt tartomány egy pontja körül egy gyök öt sugarú kört rajzolunk, az az egész tartományt lefedi, így hat pont nem rakható le a téglalapon belül úgy, hogy bármely kettő távolsága legalább gyök öt legyen.
|
 |
| Előzmény: [638] fermel, 2007-02-17 14:42:37 |
|
| [661] trizi | 2007-02-28 15:17:12 |
 epsilon! már meg is van az eredmény, köszi
|
|
| [660] epsilon | 2007-02-28 14:17:06 |
 Bizonyára tudod, hogy a körszelet területe T=r×r×(x-sinx)/2. Legyen O a kőr középpontja, AB a 210 cm hoszú húr, és legyen OM merőleges az AB húrra, M a talppont az AB húron. Legyen r a kör sugara, így pl. az OAB derékszögü háromszögben az átfogó r, a két befogó 105 illetve (r-50). Pitagorász tételével innen kijön az r. Továbbá az OAB háromszög területét 2 féle képpen felírjuk: 1/2×AB×OM=1/2×OB×OC×sinx vagyis 210×(r-50)=r×r×sinx és innen az r ismeretében megvan sinx és aztán x is.
|
|
| [659] trizi | 2007-02-28 12:36:49 |
 Sziasztok. Tud valaki segíteni körszelet területének kiszámításában, ha m=50 cm h=210 cm és más adatot nem ismerek?
|
|
| [658] jenei.attila | 2007-02-27 14:59:55 |
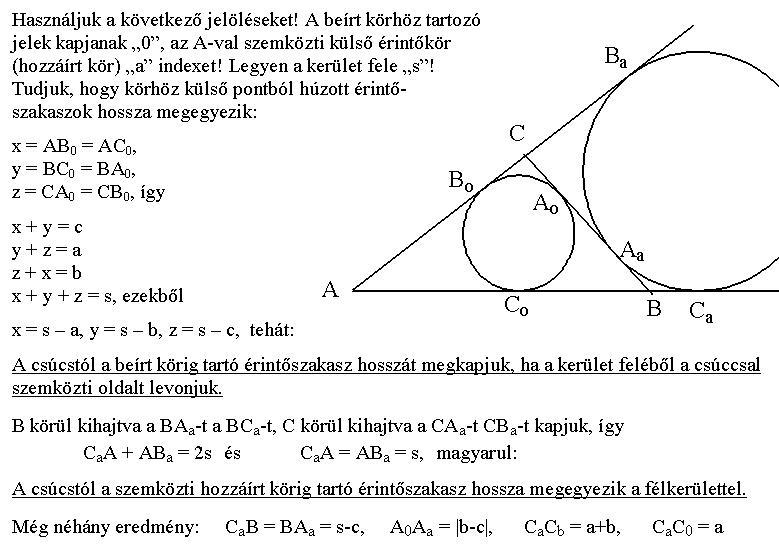
 A feltételből következik, hogy a szemközti oldalak hosszának összege egyenlő. Mivel konvex négyszögről van szó, ezért a négyszög érintő négyszög. Érintő négyszögben az egyik átló behúzásával keletkező két háromszög beírt körei érintik egymást. Ez csak vázlat, de nagyon könnyű bizonyítani ezeket az állításokat.
|
| Előzmény: [653] Csimby, 2007-02-23 01:20:45 |
|
| [657] HoA | 2007-02-26 16:03:28 |
 Javaslom 107. feladat nak [656] általánosítását: Bizonyítsuk be, hogy egy sokszöglapon két pont távolsága (a pontok a határon is lehetnek) nem lehet nagyobb, mint a sokszög két, egymástól legtávolabbi csúcsának távolsága.
|
| Előzmény: [656] fermel, 2007-02-25 13:01:40 |
|
| [656] fermel | 2007-02-25 13:01:40 |
 A 638-asban leírt feladattal kapcsolatban lenne még kérdésem. Azt kellene belátni, hogy egy 2x2-es házikóban(2x1-es téglalapon egy 2 alapú, 1 magasságú egyenlőszárú háromszög)két pont távolsága maximum négyzetgyök 5.(természetesen a pontok a határon is lehetnek) Köszönöm: fermel
|
| Előzmény: [638] fermel, 2007-02-17 14:42:37 |
|
|
|
| [653] Csimby | 2007-02-23 01:20:45 |
 106.feladat Egy konvex négyszög egyik átlóját behúzva, a kapott két háromszög beírható körei érintik egymást. Bizonyítsuk be, hogy a másik átlót behúzva ugyanez igaz. (Ma volt Arany Dani feladat 9.oszt.-osoknak)
|
|
| [652] BohnerGéza | 2007-02-23 00:42:22 |
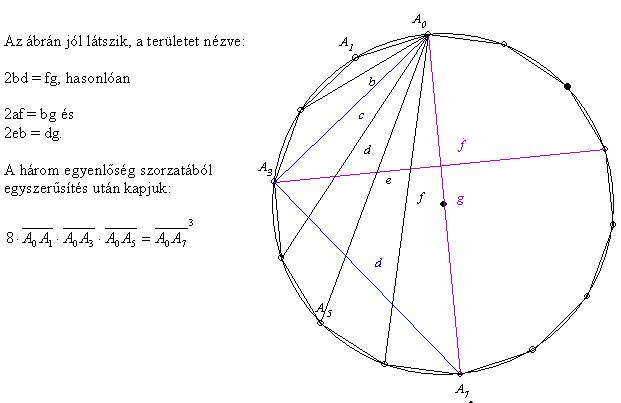
 Köszönöm nadorp [642] tanulságos megoldását! Azt hiszem, ez és az alábbi alapján is kitalálhatunk új feladatokat.
A feladatra a B.3970 ([632]-ben is megtalálható) megoldásának keresése közben találtam, egy átmérő behúzása után a következőt észrevéve:
|
 |
| Előzmény: [639] BohnerGéza, 2007-02-18 00:54:57 |
|
|
|
|
| [648] HoA | 2007-02-22 15:52:27 |
 Nagyon szép megoldás!
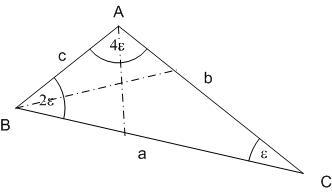
Azért leírom, szerintem mire gondoltak a feladat kitűzöi. Tekintsük a szabályos hétszög oldala és két különböző átlója által alkotott ABC  -et . -et . 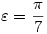 , ,  =4. =4. , , =2. =2. , , = = . Vegyük észre, hogy mind az . Vegyük észre, hogy mind az  mind a mind a  szög felezője a szög felezője a  -et egy, az eredetihez hasonló és egy egyenlőszárú -et egy, az eredetihez hasonló és egy egyenlőszárú  -re bontja. Az elsőből -re bontja. Az elsőből 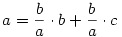 , a2=b2+bc , a másodikból , a2=b2+bc , a másodikból 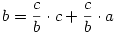 , b2=c2+ac . Felhasználva, hogy c=1 , b2=c2+ac . Felhasználva, hogy c=1
(1) -ben a-t (2) -ből helyettesítve: (b+1)2.(b-1)2=b2+b=b.(b+1)
| a+b=(b+1)(b-1)+(b+1)(b-1)2=(b+1)(b-1)(1+b-1)=(b+1)(b-1)b | (5) |
végül
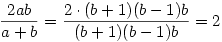 | (6) |
|
 |
| Előzmény: [646] BohnerGéza, 2007-02-22 11:51:37 |
|
|








 szöggel) emelkedő csavarvonalnak?
szöggel) emelkedő csavarvonalnak?





 -et .
-et .  ,
, =2.
=2. =
=