| [821] epsilon | 2007-07-26 14:06:03 |
 Helló Károly! Igen, úgy van ahogyan mondod. Kiváltképpen az érdekelne, hogy ennek a konvex buroknak a térfogatának az értéke a kocka térfogatának hányad részével lehet egyenlő, és esetleg mely értékeket nem veheti fel a kocka térfogatából? Üdv: epsilon
|
| Előzmény: [820] Hajba Károly, 2007-07-24 23:50:31 |
|
| [820] Hajba Károly | 2007-07-24 23:50:31 |
 Üdv!
Egy naív kérdés, ellenőrzésképpen, hogy jól értem-e.
A 12 pont konvex burka az a kockából visszamaradó idom, melyet úgy kapunk, hogy a 8 sarkából tetraédereket levágunk, s egy-egy szomszédos csúcshoz tartozó tetraéderek megfelelő csúcspontjaik a kijelölt pontban azonosak?
Ha igen, akkor a következő -vizuális úton nyert- meglátásaim vannak: Ekkor az idom mindenképpen konvex. Szélsőséges esetben legfeljebb három pont a csúcsban lehet azonos is. Maximális térfogata egységnyi, míg minimális térfogata harmad egységnyi.
|
| Előzmény: [816] epsilon, 2007-07-24 09:16:24 |
|
| [819] epsilon | 2007-07-24 21:55:31 |
 Helló Cckek! Itt vannak nekem is kételyeim, hogy minden esetben felvehető-e úgy a 12 pont, hogy a szóbanforgó test konvex legyen? Na persze, ha még térfogati megszorítások, kitétek is bekerülnek, akkor még áltáthatatlanabb. Nyilván a "konvex burok" csak ekkor illik a szóhasználatra!
|
| Előzmény: [817] Cckek, 2007-07-24 10:09:12 |
|
| [818] jonas | 2007-07-24 11:24:51 |
 Ez egy másik feladatra emlékeztet a Pólya-Szegő analízis feladatgyűjteményből, amit feladtunk a szemináriumon. Sajnos miután utánanéztem, kiderült, hogy nem segít ehhez a feladathoz, mert a térfogatról nem mond semmit. Ide másolom a feladatsorról
Legyen a 3-térben egy test olyan tulajdonságú, hogy szakaszban vagy pontban (vagy az üres halmazban) metsz minden, a koordinátatengelyek bármelyikével párhuzamos egyenest. Legyen a test vetülete a koordinátasíkokra P, Q, illetve R területű. Legyen a test felszíne A. Lássuk be, hogy
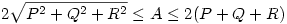
Igazoljuk, hogy a becslés éles.
|
| Előzmény: [816] epsilon, 2007-07-24 09:16:24 |
|
|
| [816] epsilon | 2007-07-24 09:16:24 |
 Helló! A következő kérdésem lenne: ha egy kocka minden élén felveszünk 1-1 pontot, mi lesz a 12 pont konvex burka, esetleg meg lehetne-e mondani a térfogatának szélsőértékeit, vagy azokat az értékeket amiket ez felvehet ? Előre is kösz Mindenkinek! Üdv: epsilon
|
|
| [815] BohnerGéza | 2007-07-22 19:59:21 |
 Az előző hozászólásomban helyesen a 122. feladat kell legyen.
Elnézést kérek ,,Lajos Arpad´´-tól, akinek érdekes a 121. feladata. Annak megoldására kiváncsi vagyok. Ebben a hőségben inkább azt hiszem, nem speciális esetben nincs rá olyan képlet, melybe egy pont koordinátáját helyettesítve megkapjuk, hogy az fényes vagy sem.
|
| Előzmény: [814] BohnerGéza, 2007-07-22 19:22:10 |
|
|
| [813] Lajos Arpad | 2007-07-21 10:23:16 |
 A 121. feladat Hmmm... Igazad van. Ezek szerint nem volt olyan nagy kudarc hogy nekem nem sikerült ;). Nekem csak egy szép integrál jött ki, amit nem igazán tudtam megoldani annak ellenére, hogy próbálkoztam egy ideig. Egy érdekes feladat: Adott egy origó középpontú ellipszis, egyenlete: (x/a) 2 + (y/b) 2 = 1 Ezen az ellipszisen teljes visszaverôdés figyelhetô meg. Az ellipszis egyik pontjáról valamilyen irányba(az ellipszis belseje felé) elindítunk egy fénysugarat, melynek szélessége elhanyagolható, és a végtelenségig verôdik az ellipszis falán vissza. A kiindulópont legyen M(x0,y0), az irány pedig alfa az origóhoz képest. A fénysugár a végtelenségig verôdik vissza az ellipszis falán. A kérdés az, hogy (a,b,X0,Y0,alfa) függvényében hol lesz fényes az ellipszis belseje? Bevallom ôszintén, hogy én ezen a problémán kb. 3 hónapig gondolkodtam hetedmagammal ameddig egy valamennyire elfogadható megoldást találtam. Jelölés : : hatvány
|
|
|
|
| [810] Lajos Arpad | 2007-07-21 06:54:06 |
 üdv mindenkinek, lenne egy kérdésem. Tudjuk hogy az ellipszis kerülete=pi*a*b, ahol a az ellipszis szélessége "a", hosszúsága pedig "b".Hogyan kéne bizonyítani? Meg próbáltam oldani a hozzá tartozó elliptikus integrált, de beletörött a bicskám.
|
|
|
| [808] sakkmath | 2007-07-16 18:26:43 |
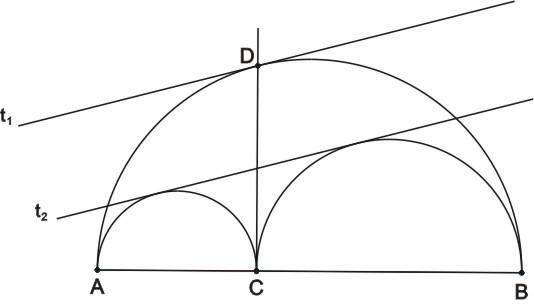
 A 120. feladat (ujjgyakorlat is lehetne):
Legyen adott az AB szakasz, melynek tetszőleges belső pontja C. Az AB, AC, CB szakaszok, mint átmérők fölé - azonos partjukra - félköröket rajzoltunk. Az AB-re C-ben állított merőleges D-ben metszi az AB félkört. Az AB félkör D-hez tartozó érintője t1, a másik két félkör közös (CD-től különböző) érintője t2. Bizonyítsuk be, hogy t1 párhuzamos t2-vel.
|
 |
|
| [807] BohnerGéza | 2007-07-14 01:45:23 |
 Köszönöm HoA szép megoldását! Egy kiegészítés és egy javaslat még:
A 119. feladat feltételei, "ha ezek léteznek és nem nullák", miatt [806]-ban a megoldást így kezdtem volna: Egyenlő szárú háromszögben az állítás igaz, különben ... . Természetesen ez nyilvánvaló, de versenyen akár helyezés múlhat azon, ha leírjuk.
Javaslom, hogy a 118. feladatban szereplő eredeti 3 pontnak az ABC valamelyik oldalára eső vetületére számoljuk ki az osztóviszonyt róval és r-rel. ( beírt, körülírt kör sugara ) Használjuk ki, hogy egy csúcsból a magasságpontba mutató vektor kétszerese a körülírt kör kp-jából a csúccsal szemközti oldalfelező pontba mutató vektornak!
|
| Előzmény: [806] HoA, 2007-07-13 17:12:29 |
|
| [806] HoA | 2007-07-13 17:12:29 |
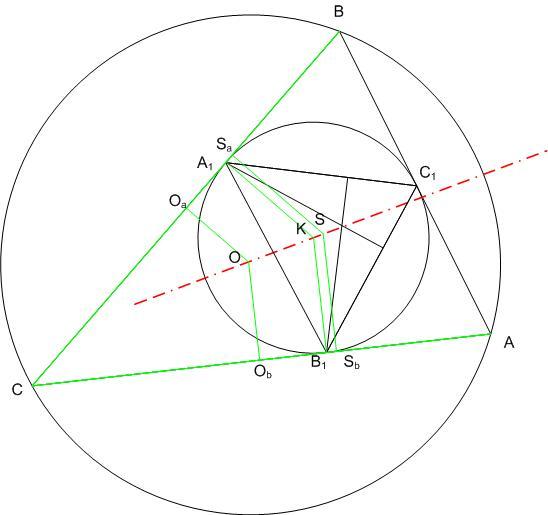
 118. feladat: [803] és [805] alapján elég azt megmutatni, hogy az O, K pontoknak és az A1B1C1 S súlypontjának az a illetve b oldalakra eső Oa,A1,Sa és Ob,B1Sb vetületeire teljesül: S súlypontjának az a illetve b oldalakra eső Oa,A1,Sa és Ob,B1Sb vetületeire teljesül: 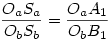 . COa=a/2,CA1=s-c, így OaA1=s-c-a/2=(b-c)/2. hasonlóan ObB1=(a-c)/2 . A kettő hányadosa (b-c)/(a-c) . COa=a/2,CA1=s-c, így OaA1=s-c-a/2=(b-c)/2. hasonlóan ObB1=(a-c)/2 . A kettő hányadosa (b-c)/(a-c)
CSb felírható mint a CA1,CB1ésCC1 szakaszok b-re eső vetületeinek számtani közepe, így ObSb=CSb-COb=1/3((s-c).cos +(s-c)+a.cos +(s-c)+a.cos +(b-a.cos +(b-a.cos )*((s-a)/c))-b/2. Itt 2s = a+b+c helyettesítéssel cos )*((s-a)/c))-b/2. Itt 2s = a+b+c helyettesítéssel cos -t a koszinusztételből kifejezve átrendezéssel adódik: -t a koszinusztételből kifejezve átrendezéssel adódik:
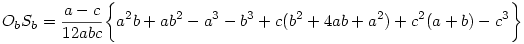
OaSa ebből a és b szerepének felcserélésével kapható. Látható , hogy a nagyzárójelben a és b szimmetrikusan lép fel, a kifejezésnek ez a része változatlan, tehát
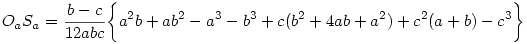
A kettő hányadosa 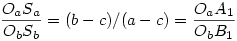
|
 |
| Előzmény: [801] BohnerGéza, 2007-06-30 23:50:41 |
|
| [805] HoA | 2007-07-09 13:52:12 |
 Még egy segítség: Mivel K az A1,B1,C1 körülírt körének középpontja, KM A1,B1,C1 körülírt körének középpontja, KM A1,B1,C1 Euler-egyenese, amin A1,B1,C1 Euler-egyenese, amin A1,B1,C1 S1 súlypontja is rajta van. Tehát elég belátnunk, hogy O,KésS1 egy egyenesen vannak. S1 súlypontja is rajta van. Tehát elég belátnunk, hogy O,KésS1 egy egyenesen vannak.
|
| Előzmény: [801] BohnerGéza, 2007-06-30 23:50:41 |
|
|
|
|
| [801] BohnerGéza | 2007-06-30 23:50:41 |
 118. feladat: A Gillis - Turán Matematikaverseny egyik szép feladatát ajánlom:
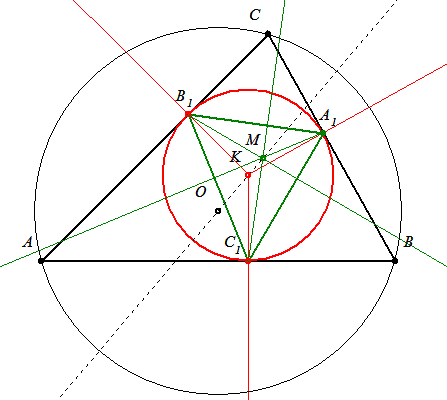
Legyen ABC egy olyan háromszög, ami nem egyenlő oldalú. Az ABC háromszög beírt köre érintse a megfelelő oldalakat az A1, B1, C1 pontokban, és legyen M az A1B1C1 háromszög magasságpontja. Bizonyítsuk be, hogy M rajta van az ABC háromszög körülírt körének középpontját és beírt körének középpontját összekötő egyenesen.
A megoldáshoz javaslom a következő segítséget:
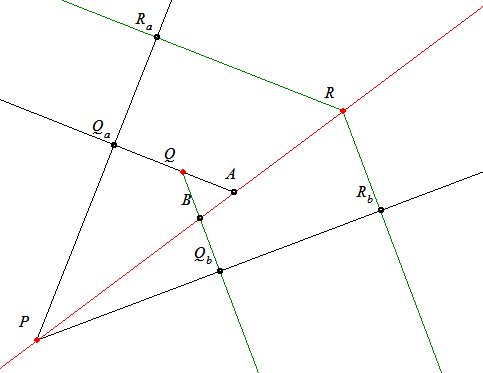
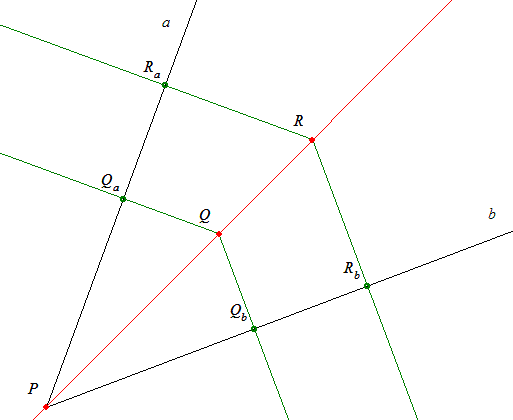
119. feladat: Legyen a P, Q és R pont merőleges vetülete az a ill. b nem párhuzamos egyenesen Pa, Qa és Ra ill. Pb, Qb és Rb. Bizonyítandó, hogy (Pa Qa Ra) = (Pb Qb Rb) -ha ezek léteznek és nem nullák- csakkor igaz, ha a P, Q és R egy egyenesen van.
/ Az egy egyenesen lévő A, B és C pontok esetén ezek osztóviszonyán értjük az (A B C)=AC/BC előjeles hányadost. /
|
|
| [800] lorantfy | 2007-06-29 15:03:41 |
 Kedves Levente!
Ügyes felvetés volt, Matyinak dicséret érte. Látom C gyakorlatokat küldött az idén. Bátorítsd egy kicsit, hogy rendszeresebben küldjön!
Üdv! Laci
|
| Előzmény: [799] klevente, 2007-06-29 11:49:08 |
|
| [799] klevente | 2007-06-29 11:49:08 |
 Kedves hozzászólók és megoldók!
A "tényleg ellipszis-e a mértani hely?" témát én vetettem volt fel. Köszönöm az érdeklődést és a problémát kimerítő megoldást.
A történet kezdetéhez annyit tennék hozzá, hogy az Árpád Gimnáziumban épp a Simson-egyenest tanítottam 9. osztályban specmaton, és a Kiss Matyi nevű (egyébként is elég tehetséges) diák állt elő ezzel a sejtéssel a GeoGebrát nézegetve. Elég ügyes intuíció, azt hiszem.
Koncz Levente
|
| Előzmény: [776] lorantfy, 2007-06-18 14:46:29 |
|
| [798] jonas | 2007-06-27 21:04:13 |
 Nos, ezeket a bolhás feladatokat az egyetemen hallottam Feladatmegoldó szemináriumon, azaz legalább négy éve. Egy másik sorozat bolhás feladat (amit most nem lövök le itt) állítólag Pósa Lajostól származik, ezért el tudom képzelni, hogy ezek is.
|
| Előzmény: [793] Hajba Károly, 2007-06-27 00:05:16 |
|
| [797] Python | 2007-06-27 15:36:56 |
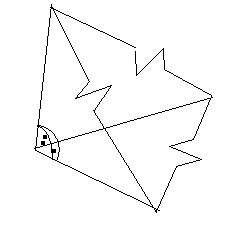
 Utolosó matekórák egyikén n=4-re láttam a feladatot, és én térbe általánosítottam:
Van 8 , az (elég gyenge) ábrán látható derékszögű triédert bevilágító, rögzített csúcsú pontszerű, átlátszó lámpánk a térben , be lehet e velük a teret világítani forgatással?
Az általános megoldásról annyit, hogy ha felvehetünk egy pontot, és abból sugarasan 360o/n fokonként félegyenest indítva, bármely 2 szomszédos félegyenes közti szögben van fényforrás, akkor n-re igaz.
(Toljunk minden cikket egy nem benne lévő pontba, így az eltolt tartalmazni fogja az eredetit, és így az n eltolt tartalmazza az n eredetit=a teljes síkot.)
|
 |
| Előzmény: [796] Sirpi, 2007-06-27 14:14:27 |
|











 S súlypontjának az a illetve b oldalakra eső Oa,A1,Sa és Ob,B1Sb vetületeire teljesül:
S súlypontjának az a illetve b oldalakra eső Oa,A1,Sa és Ob,B1Sb vetületeire teljesül:  +(s-c)+a.cos
+(s-c)+a.cos
 (PbQbRb).
(PbQbRb).