|
| [845] zizibi | 2007-08-23 11:33:56 |
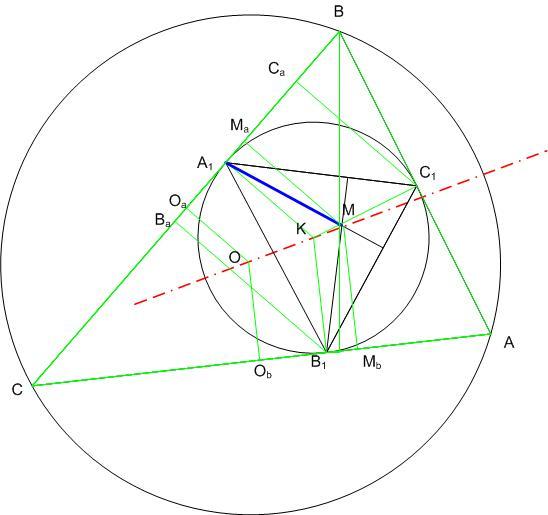
 Igen, erre az egyenletre rá jöttem én is, de kéne még egy egyenlet, gondolom, amiből ki lehet fejezni az x-t és egy másik amiből az y-t.
Na idáig nem jutottam el. Vagy az egyik koordinát egyenletét be lehetne helyettesíteni a másikba, pl. x-et kifejezve belőle?
|
| Előzmény: [842] BohnerGéza, 2007-08-22 20:45:22 |
|
|
|
|
| [841] zizibi | 2007-08-22 14:26:32 |
 Kedves BohnerGéza!
Még egyszer köszönöm az előző segítséget, remekül tudom használni (bár koordinátarsz-re nem volt szükségem, mert karakteresen működik a program), de nem igazán értem, hogy Pithagórasz-tétel hogyan is működik ebben az esetben.
Közben pedig újabb problémába ütköztem.
Szintén koordináta jellegü és az előző feladat megfordítása, vagyis adott AB egyenes és egy X pont. Meg szeretném tudni, hogy az X pont milyen merőleges távolságra van A-tól, AB egyenesen mérve illetve milyen messze van AB egyenestől.
Szögfügvényekkel találtam megoldást, de nekem jobban tetszene egy, az előzőhöz hasonló megoldás.
Előre is köszönöm a segítséget!
|
| Előzmény: [836] BohnerGéza, 2007-08-16 21:56:13 |
|
|
|
| [838] Bauer Gábor | 2007-08-21 09:53:03 |
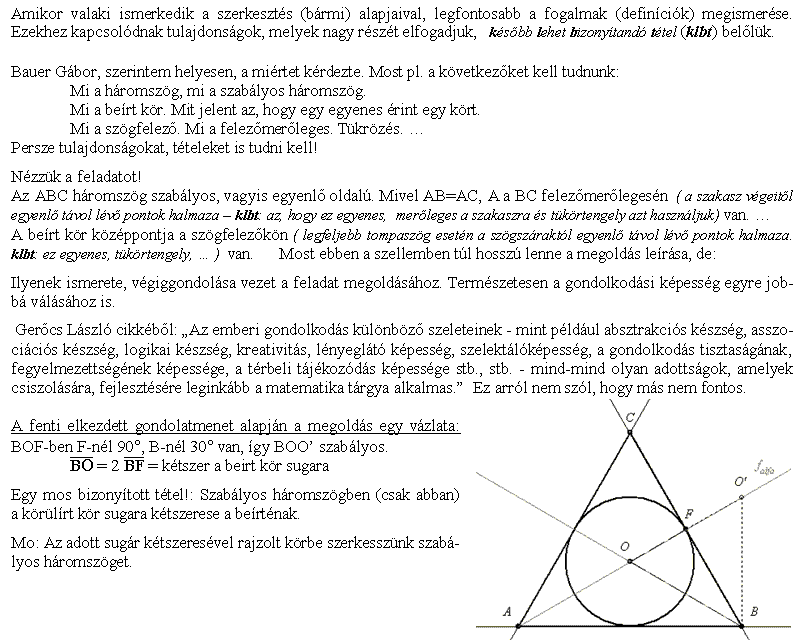
 Tisztelt Barátaim! Alapvetó problémával kerültem szembe a következő feadattal: "Szerkesszünk szabályos háromszöget ha adott a beírt kör sugara." Kérdésem a következő: Melyek azok a tételek amelyek átgondolásával a feladat megoldható és mi a szerkesztés menete? Válaszukat hálásan köszönöm.
|
|
|
|
| [835] zizibi | 2007-08-16 14:07:12 |
 Sziasztok!
Átböngésztem az eddigi hozzászólásokat, de sajnos nem találtam megoldást a problémára, aszem.
Programot szeretnék irni, de a dolgok matematikai oldalával nem igazán vagyok tisztában. Adott, korrdinátásan, két pont által meghatározott vonal. Szeretnék megkeresni egy pontot ami X távolságra van az egyik végétől rajta az egyenesen.
A másik program az lenne, hogy ugyanezen vonal egyik pontjától X távolságra és Y távolságra merőlegesen magától vonaltól lenne a pont.
Előre is köszönöm a segítséget!
|
|
|
|
|
| [831] HoA | 2007-07-30 11:43:17 |
 Ha van az enyémnél kevésbé hosszadalmas, szemléletes megoldásod, örömmel látnám. Javaslatod arra utal, hogy igen. Megpróbáltam a leírt tényt kihasználni, de megint csak az Euler egyenesre jutottam:
M - C = 2 ( ( A + B ) / 2 - O ) ; M - C = A + B - 2O ; M = A + B + C -2O = 3S - 2O
és mivel a jobb oldalon az együtthatók összege 1, ez éppen azt jelenti, hogy M, S és O egy egyenesen van.
|
| Előzmény: [807] BohnerGéza, 2007-07-14 01:45:23 |
|
| [830] epsilon | 2007-07-28 13:42:58 |
 Ok Cckek, ebben teljesen igazad van, megpróbálom a feladatot egészében "emésztgeni" Kösz, üdv: epsilon
|
|
|
| [828] epsilon | 2007-07-28 07:08:13 |
 Heló Károly és Cckek! Valójában az 1/3 egy elfajult eset, amikor pontok egybeesnek. Ha a 12 pont mind különböző, akkor az az érzésem, hogy 1/3-hoz tetszőlegesen közel lehet (?) de azt nem veszi fel? A folytonossággal értem, hogy hamar lelőhető, de többváltozó esetén van a globális meg komponensenkénti folytonosság, ezzel ezt akarom mondani, hogy még nem elég megggyőző számomra, hogy valóban bármely y az [1/3;1] értékre létezik a 12 pont kérdéses elhelyezkedése. De mindenképpen még gondolkodom, és kösz! Üdv: epsilon
|
|
|
|
| [825] Cckek | 2007-07-27 22:46:21 |
 Minden értéket felvehet:) Ugyanis az egy csúcsban összefutó három él által meghatározott tetraéder térfogata, 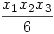 , ahol x1,x2,x3 az illető éleken felvett pontok csúcsoktól mért távolsága,a kocka térfogatának (ami 1) és nyolc ilyen tetraéder térfogata összegének a különbsége adja a konvex burok térfogatát. Tehát lesz egy 12 változós függvényünk, mely folytonos, és mint már Károly bebizonyította felveszi a 0 és az 1 értékeket tehát minden értéket [0,1]-ből. , ahol x1,x2,x3 az illető éleken felvett pontok csúcsoktól mért távolsága,a kocka térfogatának (ami 1) és nyolc ilyen tetraéder térfogata összegének a különbsége adja a konvex burok térfogatát. Tehát lesz egy 12 változós függvényünk, mely folytonos, és mint már Károly bebizonyította felveszi a 0 és az 1 értékeket tehát minden értéket [0,1]-ből.
|
| Előzmény: [824] epsilon, 2007-07-27 17:54:59 |
|
| [824] epsilon | 2007-07-27 17:54:59 |
 Köszi Károly! Ilyesmi érdekelne, hogy a konvex burok térfogata lehet pl. 2/3, továbbá milyen értékeket vehet fel a (0,1) intervallumban. Előreis kösz, üdv: epsilon
|
|
| [823] Hajba Károly | 2007-07-26 22:58:55 |
 Ha minden pont oly módon van valamely csúcsban, hogy minden csúcsra kerül pont, akkor a konvex burok nyilvánvalóan megegyezik a kockával. Ha a kocka térfogatát egységnyinek veszem, akkor a burok maximális térfogata 1 egység.
Ha a pontokat úgy próbáljuk a csúcsokan elhelyezni, hogy minél kevesebb csúcson jelenjenek meg, akkor a 4 csúcs a lapok átellenes (átlós) csúcsaira kerülnek, s a 4 csúcs egy szabályos tetraédert alkot. Ekkor a burok térfogata 1/3 egység.
Nem erősségem a bizonyítás, de gyakorlatilag ez utóbbi a minimális térfogat.
|
| Előzmény: [821] epsilon, 2007-07-26 14:06:03 |
|
|



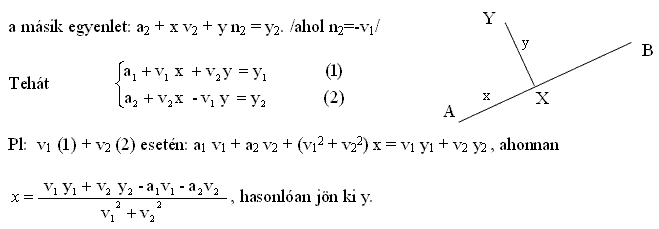







 .sin
.sin . Hasonlóan, mivel KC1 merőleges c-re, A1Ca=
. Hasonlóan, mivel KC1 merőleges c-re, A1Ca= . Innen A1Ma=
. Innen A1Ma= -sin
-sin