|
| [871] SmallPotato | 2007-10-07 11:47:14 |
 Néhány kiegészítés:
1.) Az eredeti 123. feladatban a hatványvonal a k1 és k2 érintési pontjában húzható közös érintő.
2.) Az előző hsz-ban leírt bizonyítás a rajzolt viszonyokon túl kiterjed az egymást érintő és az egymást metsző k1 és k2 körök esetére is. Ezekben az esetekben a hatványvonal rendre k1 és k2 közös belső érintője (értelemszerűen a körök egyetlen közös pontján át), ill. a körök metszéspontjain át húzható egyenes.
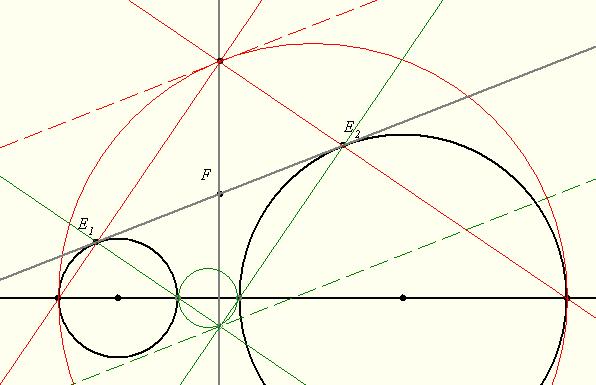
3.) Ha k1 és k2 nem érinti egymást, akkor (akár 0, akár 2 közös pontjuk van) az általuk "közrefogott" C1C2 átmérőjű körhöz G pontban húzható érintő is természetesen párhuzamos e-vel, e1-gyel és e2-vel. G aszerint helyezkedik el a közös átmérőegyenesnek a D felőli ill. azzal ellentétes oldalán, hogy k1 és k2 közös pontjainak száma 2 vagy 0.
|
| Előzmény: [870] SmallPotato, 2007-10-07 01:14:42 |
|
| [870] SmallPotato | 2007-10-07 01:14:42 |
 Megoldás a 124. feladatra.
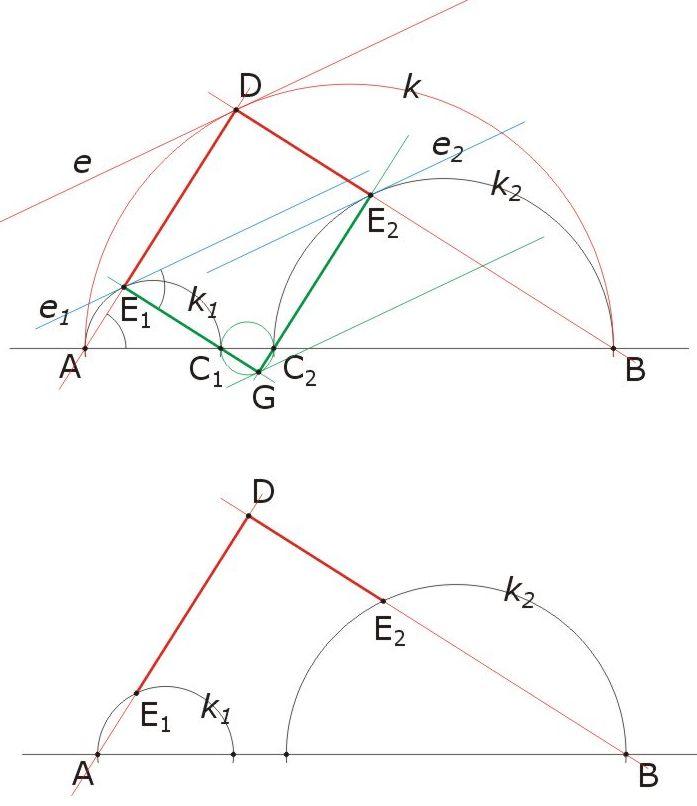
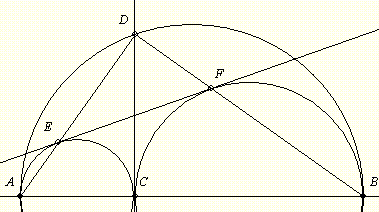
Rajzoljunk egy - szándékosan "elrontott" - ábrát, azaz egy olyat, ahol a találomra választott D pontból húzott DA és DB egyenesek által a k1 ill. k2 körökből kimetszett E1 és E2 pontok nem a közös érintő érintési pontjai!
Ebből az ábrából is megállapíthatjuk a következőket:
1.) Ha D a k kör pontja, akkor a jelölt e, e1 és e2 érintők párhuzamosak, hiszen k1-et A-ból, k2-t B-ből kellő arányban nagyítva a k1 ill. k2 körök k-ba, az E1 ill. E2 pontok D-be, tehát az e1 ill. e2 egyenesek e-be mennek át.
2.) A Thalész-tétel megfordítása értelmében az AC1E1, ABD és C2BE2 háromszögek derékszögűek (így hasonlóak is), és a vastagítva rajzolt DE1GE2 négyszög téglalap.
3.) A jelölt C1AE1 és C1E1e1 szögek egyenlőek, mert mindkettő a k1 kör C1E1 ívén nyugvő kerületi szög (utóbbi érintőszárú).
4.) Ezek szerint e1 és e2 akkor esik egybe, ha a jelzett DE1GE2 téglalapban pl. az E2E1D szög a jelzett szög pótszöge, azaz - a korábban említett háromszög-hasonlóságokat figyelembe véve - ha pl. 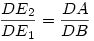 . .
Az utóbbi egyenlőséget átrendezve (az alsó ábrán csak a lényeg van kiemelve): DB*DE2=DA*DE1, azaz e1 és e2 akkor és csak akkor esik egybe, ha a D pont hatványa a k1 és k2 körökre azonos. Ez akkor és csak akkor teljesül, ha D pont a k1 és k2 körök hatványvonalán van. A hatványvonal ismert tulajdonsága, hogy adott pontjából a két körhöz egyenlő hosszú érintőszakaszok húzhatók (ha egyáltalán húzhatók), tehát (egyebek közt) a 124. feladat eredeti ábráján az F pontból is.
|
 |
| Előzmény: [857] BohnerGéza, 2007-09-20 11:08:40 |
|
| [869] farkasb | 2007-10-05 03:01:23 |
 Köszönöm, ez a 3. megoldás nagyon jó! Persze elismerésem a másik kettőért is :)
|
|
| [867] HoA | 2007-10-04 17:01:42 |
 Tovább egyszerűsíthető a megoldás, ha a koordinátarendszer kezdőpontját x0 -ba helyezzük át. Ekkor a  két oldalvektora a=x1-x0=(-0,1693;-0,7763;-1,7028) és b=x2-x0=(-2,7655;-1,4626;0,8991) . A két oldalvektora a=x1-x0=(-0,1693;-0,7763;-1,7028) és b=x2-x0=(-2,7655;-1,4626;0,8991) . A  síkját e két vektor feszíti ki, így R felírható síkját e két vektor feszíti ki, így R felírható
R=x.a+y.b..........(1)
alakban. R az oldalfelező merőlegeseken van, tehát (R-0)a=(a-R)a , a(2R-a)=0 és hasonlóan b(2R-b)=0 . (1) -ből R felbontását a két utóbbi egyenletbe helyettesítve és rendezve kapjuk:
2.a2.x+2.ab.y=a2 ; 2.ab.x+2.b2.y=b2
Látható, hogy a numerikus számításhoz csak az a2,b2 és ab értékekre van szükségünk, ezek rendre 3,53083202 ; 10,59556982 ; 0,07262805 . A megoldás - például az egyenlő együtthatók módszerével
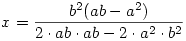 ; ; 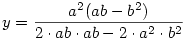
Numerikusan x = 0,489784223 ; y = 0,496642741 , amiből R = (-1,45639 ; -1,10661 ; -0,38747 ) . Visszatérve az eredeti koordináta rendszerre ezt x0 -hoz hozzáadva a várható r=(0,037714;-0,96211;0,532327) eredményt kapjuk.
|
| Előzmény: [866] jonas, 2007-10-04 11:57:49 |
|
| [866] jonas | 2007-10-04 11:57:49 |
 Most nézzük ugyanerre az egyszerűbb megoldást.
Legyen tehát a háromszög három csúcsába mutató vektor
x0=(1.4941,0.1445,0.9198)
x1=(1.3248,-0.6318,-0.7830)
x2=(-1.2714,-1.3181,1.8189)
Egyszerűen kiszámoljuk két csúcs felezőmerőleges síkját, aztán egy másik két csúcs felezőmerőleges síkját is (a harmadik nem kell), majd a csúcsok síkját, végül ezek metszetét.
Az a és b pontok felezőmerőleges síkjának egyenpete 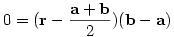 , átalakítva r(b-a)=(a+b)(b-a)/2. , átalakítva r(b-a)=(a+b)(b-a)/2.
Speciálisan a x0 és x1 csúcsok felezőmerőleges síkjának koordinátái
x1-x0=(-0.1693,-0.7763,-1.7028)
(x0+x1)(x1-x0)/2=-0.1659
Hasonlóan x1 és x2 csúcsoké
x2-x1=(-2.5962,-0.6863,2.6019)
(x1+x2)(x2-x1)/2=1.9474
A három csúcs síkját pedig egy 4 méretű homogén lineáris egyenletrendszerből kapjuk meg. Ha a sík egyenlete pr=q, akkor ebben xi rajta fekszik, így 0=pxi-q, amit meg kell oldani a p,q négy változóra. Ennek a megoldását például a Cramer-szabályból kapjuk meg: q a csúcsokból álló mátrix determinánsa, p pedig azoknak a mátrixoknak a determinánsa, amit ez előbbi mátrixból egy oszlop 1-re cserélésével kapunk.
p=(-3.1885,4.8613,-1.8992)
q=-5.8084
Most már csak el kell metszenünk a három síkot. Ehhez az alábbi egyenletrendszerünk van:
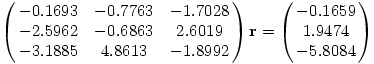
Ezt megoldva
r=(0.0377,-0.9621,0.5323)
ami szépen egyezik az előző megoldással.
|
|
|
| [864] jonas | 2007-10-02 16:57:08 |
 Nézzünk egy példát.
Vegyük azt a háromszöget, aminek a csúcsainak koordinátái
x0=(1.4941,0.1445,0.9198)
x1=(1.3248,-0.6318,-0.7830)
x2=(-1.2714,-1.3181,1.8189)
Ekkor az oldalak vektorai
v0=x1-x2=(2.5962,0.6863,-2.6019)
v1=x2-x0=(-2.7655,-1.4626,0.8991)
v2=x0-x1=(0.1693,0.7763,1.7028)
Most számoljuk ki az oldalak által bezárt szögeket az oldalvektorok skalárszorzatából.
|v1|=3.25512
|v2|=1.87908
(v1,v2)=-0.0726366
cos ( - - 0)=(v1,v2)/(|v1|.|v2|)=0.0118753 0)=(v1,v2)/(|v1|.|v2|)=0.0118753
 - - 0=1.58267 0=1.58267
 0=1.55892 0=1.55892
Hasonlóan
 1=1.05618 1=1.05618
 2=0.52649 2=0.52649
Ebből
sin (2 0)=0.0237489 0)=0.0237489
stb, amiből a körülírt kör középpontjába mutató vektor
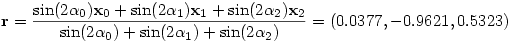
Ennek a távolsága valóban minden csúcstól ugyanannyi:
r=|r-x0|=|r-x1|=|r-x2|=3.49585
és a r-bfxi vektorok lineárisan összefüggők, azaz a pont a háromszög síkjában van, tehát ez valóban a háromszög középpontja.
|
| Előzmény: [863] jonas, 2007-10-02 15:37:50 |
|
| [863] jonas | 2007-10-02 15:37:50 |
 Igen, noha fejből nem tudtam megmondani. Súlyozni kell a csúcsokat a csúcsban lévő szög kétszeresének a színuszával, és normálni ezeknek az összegével.
|
| Előzmény: [861] farkasb, 2007-10-02 00:06:56 |
|
| [862] Lóczi Lajos | 2007-10-02 13:29:35 |
 Minden attól függ, hogy milyen matematikai szövegkörnyezetben vagyunk. Pl. a háromszög is tekinthető körnek (és viszont), ha topológiai szemmel nézzük a dolgokat, ahol is csak a folytonos egymásba deformálhatóság számít.
|
| Előzmény: [860] Pokolfajzat, 2007-10-01 20:21:37 |
|
| [861] farkasb | 2007-10-02 00:06:56 |
 Tisztelt Fórumozók!
Érdeklődnék, hogy valaki tud-e képletet egy egy térbeli háromszög köré írható kör középpontjának kiszámítására, és a térbeli kör egyenletének felállítására. Előre is köszönettel: F.Balázs
|
|
| [860] Pokolfajzat | 2007-10-01 20:21:37 |
 Nincs különösebb jelentősége, csak részemről volt ez egy feltevés, másoknak. Akik azt mondták erre, hogy ez nem igaz, csakhogy az igazamat én sem tudtam ésszerűen alátámasztani. És reméltem, ha a feltevésem igaz akkor itt talán tudnak rá egyesek magyarázatot is adni.
|
|
|
| [858] Pokolfajzat | 2007-09-22 19:44:13 |
 Csak egy kérdéssel zavarnám meg a tisztes társaságot. Előre is elnézést kérek, ha banális vagy ostoba lenne a kérdés. Tekinthető e a kör egy végtelen sokszögnek? Előre is köszönöm.
|
|
|
| [856] SmallPotato | 2007-09-20 08:39:23 |
 Felhozom kicsit a topikot.
A 123. feladat megoldása:
Kicsinyítsük az AB átmérőjű kört A-ból 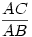 arányban! Ekkor a D pont képe E, AB kör D-beli érintőjének képe pedig AC kör E-beli érintője lesz; e két érintő (a kicsinyítés tulajdonságaiból adódóan) párhuzamos. arányban! Ekkor a D pont képe E, AB kör D-beli érintőjének képe pedig AC kör E-beli érintője lesz; e két érintő (a kicsinyítés tulajdonságaiból adódóan) párhuzamos.
A 120-as feladat megoldásából azonban ismert, hogy a rajzolt elrendezésben az AB kör D-beli érintője párhuzamos az AC és a CB körök közös külső érintőjével. Eszerint AC kör imént előállt (E pontbeli) érintője ezzel a közös érintővel egybeesik.
(Természetesen elindulhattunk volna az AB kört C-ből 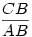 arányben kicsinyítve is.) arányben kicsinyítve is.)
|
| Előzmény: [854] BohnerGéza, 2007-09-05 23:57:21 |
|
|
|
| [853] sakkmath | 2007-08-30 09:20:48 |
 Köszönöm, hogy foglalkoztál a feladattal és feltetted a megoldásodat, ami természetesen helyes.
A feladat egyébként - elemi módon - még (legalább) két másik módszerrel is megoldható. Tehát nincs még lelőve semmi, aki esetleg új megoldásra bukkan, nyugodtan tegye fel...
|
| Előzmény: [851] SmallPotato, 2007-08-29 23:34:51 |
|
|
| [851] SmallPotato | 2007-08-29 23:34:51 |
 A 808-asra hoznék egy megoldást; úgy látom, eddig még nem érkezett.
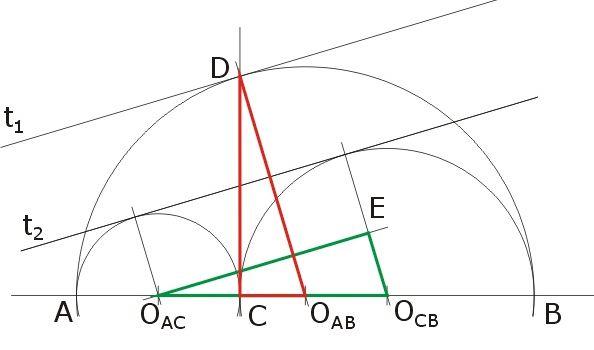
Legyen 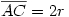 , és , és 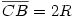 . .
Húzzunk párhuzamost t2-vel az OAC ponton át; messe ez a BC átmérőjű körnek a t2-vel való érintési pontjába húzott sugarát az E pontban. Ekkor 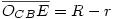 és az OACOCBE háromszög E szöge derékszög, átfogója pedig R+r. és az OACOCBE háromszög E szöge derékszög, átfogója pedig R+r.
Az OABDC háromszög C szöge derékszögű, 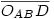 átfogója (lévén az átfogója (lévén az  átmérőjű kör sugara) szintén R+r, és átmérőjű kör sugara) szintén R+r, és 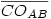 befogója szintén R-r, tehát befogója szintén R-r, tehát
az OACOCBE és a OABDC háromszögek egybevágók.
Eszerint viszont COABD =OACOCBE =OACOCBE , azaz , azaz 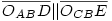 , és mivel az érintők merőlegesek a megfelelő sugarakra, t1||t2. , és mivel az érintők merőlegesek a megfelelő sugarakra, t1||t2.
|
 |
| Előzmény: [808] sakkmath, 2007-07-16 18:26:43 |
|
| [850] zizibi | 2007-08-24 18:31:31 |
 Köszönöm, segítséget. Így már értem.
Az az igazság ogy a 10. volt már majd 10 éve volt, de nem is azzal van a gond csak nem esett le az egyenlő együtthatók módszer.
Mégegyszer köszönöm! :)
|
| Előzmény: [849] BohnerGéza, 2007-08-24 16:29:24 |
|
| [849] BohnerGéza | 2007-08-24 16:29:24 |
 A számolásnál az egyenlő együttgatók módszerét használtam. Ha elvégezted volna a jelzett számolást, észrevetted volna, hogy y kiesik.
Próbáld ki! Az első egyenletet v2-vel, a másodikat v1-gyel szorozva, a kettőben x ua-szor lesz. Kivonva egymásból a kapott egyenleteket x kiesik, y kiszámolható.
Természetesen behelyettesítéssel is kijön ue.
Ezeket legalább tizedikes ismerőseidtől is megtudhattad volna.
|
| Előzmény: [848] zizibi, 2007-08-24 09:41:49 |
|
| [848] zizibi | 2007-08-24 09:41:49 |
 Hát igen, én bonyolultabban akartam megoldani :)
De azt nem igazán értem, hogy ha megszorzom az egyik egyenletet v1 a másikat v2-vel, akkor hova tűnik az y? Mert hát ha jól emlékszem, hiányos matektudásomban az van, hogy minden tagot szorozni kell, vagy nem? Ez valamiféle egyszerűsítés?
Elnézést, hogy ennyit értetlenkedem, de szeretném megérteni hátha jobban felfogom...
|
| Előzmény: [846] BohnerGéza, 2007-08-23 14:09:27 |
|
|







 két oldalvektora a=x1-x0=(-0,1693;-0,7763;-1,7028) és b=x2-x0=(-2,7655;-1,4626;0,8991) . A
két oldalvektora a=x1-x0=(-0,1693;-0,7763;-1,7028) és b=x2-x0=(-2,7655;-1,4626;0,8991) . A 
 -
- 0)=(v1,v2)/(|v1|.|v2|)=0.0118753
0)=(v1,v2)/(|v1|.|v2|)=0.0118753

 =OACOCBE
=OACOCBE
