| [971] Bubóka | 2008-01-04 08:23:54 |
 Elnézést lehet kérni, de lehet párhuzamost húzni vonalzóval!!!!!! Adott ponton át adott egyenesre, "trapéz feladat" segítségével! Én úgy gondolom, hogy azért mert valaki valamit nem tud az nem egyenlő azzal, hogy olyan nem létezik.
Nem tévedés volt a merőleges. Biztos hogy lehet, csak én nem jövök rá egyenlőre a menetére.
|
| Előzmény: [970] jonas, 2008-01-03 22:17:18 |
|
|
| [969] S.Ákos | 2008-01-03 21:21:58 |
 Így hirtelen nem látom, hogy párhuzamost hogy lehetne csak vonalzóval szerkeszteni. Felvilágosítanál?
Bubóka: Az 5-szög szerkesztése meg abból következik, hogy az egységnyi sugarú körbe írt 10szög oldala 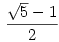 . Ez pithagorasz-tétel segítségével meg könnyen szerkeszthető. . Ez pithagorasz-tétel segítségével meg könnyen szerkeszthető.
|
| Előzmény: [968] jonas, 2008-01-03 19:31:17 |
|
| [968] jonas | 2008-01-03 19:31:17 |
 "Hogy kell pontból egyenesre merőlegest bocsátani CSAK vonalzóval?"
Nem párhuzamosra gondolsz véletlenül? Ha nem, akkor nincs valami más is adva? Mert így lehetetlen.
|
| Előzmény: [967] Bubóka, 2008-01-03 18:22:34 |
|
| [967] Bubóka | 2008-01-03 18:22:34 |
 Üdv Mindenkinek! Segítségeteket szeretném kérni. Hogy kell pontból egyenesre merőlegest bocsátani CSAK vonalzóval? HA a menetét valaki leírná, nagyon megköszönném. Ja! És szabályos ötszöget szerkeszteni az aranymetszéssel...?
|
|
| [966] BohnerGéza | 2008-01-02 22:51:56 |
 129. feladat: Az ABCD négyszög nem trapéz. AB és CD az E-ben metszik egymást. Az ADE és BCE körülírt köre E-n kívül F-ben találkoznak. Bizonyítandó, hogy ABF és CDF hasonlóak!
|
|
|
| [964] BohnerGéza | 2007-12-31 14:05:01 |
 A megkötés valóban nem kell, a kitűzők talán a 9-eseknek szóló feladatot "nehezítették", lehessen általánosítani. A korosztálytól nem feltétlenül trigonometriát használó megoldást vártak. Az elemi tetszett nekem jobban.
|
| Előzmény: [963] SmallPotato, 2007-12-30 19:30:47 |
|
| [963] SmallPotato | 2007-12-30 19:30:47 |
 A megoldás szerintem is helyes. (Pontosabban: nekem is ez jött ki. :-) )
Két hozzáfűznivalóm lenne azért:
A feladat kifejezetten hegyesszögű háromszöget ír; Te nem ilyet rajzoltál, bár elsőre nekem sem tűnik lényeginek a megkötés. (Majd lehet, hogy engem is helyreigazítanak. :-D)
A másik: a jövőre nézve szerencsésebb lenne (mivel megszokott), ha a háromszög csúcsait az óramutató járásával ellentétes sorrendben betűznéd, és a szögeket ugyanezen sorrendben osztanád ki (az A csúcsban  , a B csúcsban , a B csúcsban  stb.) stb.)
Azért merem ezt kérni, mert emlékszem első táblai geometria-szereplésemre a gimiből: nem szokványosan betűztem a háromszöget, és a padsorokból tömény húúúúúú jött ... :-)))
|
| Előzmény: [962] S.Ákos, 2007-12-30 12:06:40 |
|
|
| [961] BohnerGéza | 2007-12-30 01:01:09 |
 A komáromi Selye János Magyar Tannyelvű Gimnázium Cornides István Emlékversenyének ( 2007.12.07 ) egy szép feladatát ajánlom:
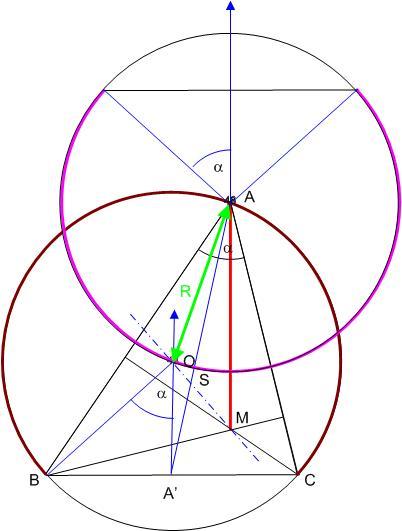
128. feladat: Az ABC hegyesszögű háromszögben az A-nál lévő szög a B-nél lévő kétszerese. A C-ben a BC-re állított merőleges AB-t D-ben metszi. Mennyi az AC / BD arány?
|
|
|
| [959] Cogito | 2007-12-14 17:02:50 |
 Kedves HoA!
A feladatot pár napja én is megoldottam, csak az idő hiányzott, hogy letisztázva közölhető állapotba hozzam. Egyetértek azzal, hogy ez a kör a keresett mértani hely abban az esetben, ha a feladatot az ABC síkra szűkítjük. A részleteket most mellőzve nekem az jött ki, hogy a mértani helynek eleget tévő P pontokra teljesül, hogy
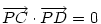 | (1) |
, ahol a C pontnak O-ra való középpontos tükörképe D. Mint látható, itt (egyrészt) azon pontok halmazáról van szó, melyekből a CD szakasz derékszög alatt látszik. Ez pedig az a C és D pontok nélküli gömbfelület, amely az Általad kapott kör CD körüli megforgatásával áll elő. Itt is igaz (másrészt) hogy a C és D pont is a mértani helyhez tartozik, hiszen a P C, vagy P C, vagy P D esetben egy-egy nullvektor miatt teljesül (1). A levezetés itt is megfordítható, tehát a teljes gömbfelület a keresett mértani hely. D esetben egy-egy nullvektor miatt teljesül (1). A levezetés itt is megfordítható, tehát a teljes gömbfelület a keresett mértani hely.
Ez az általános megoldás, hiszen a feladat szövege megengedi, hogy P-t térbeli pontnak tekintsük, a levezetés(ek) pedig ennek az értelmezésnek is eleget tesznek.
|
| Előzmény: [958] HoA, 2007-12-14 08:26:03 |
|
|
|
| [956] szegeddiák | 2007-11-28 21:32:57 |
 Sziasztok...segítségre lenne szükségem néhány feladatjoz..ha vki meg tudja oldani ezeket kérem rakja fel vagy vegye fel velem a kapcsolatot.Igazán sürgős lenne mert pénteken ebből zh-t írok.köszi előre is
tehát a feladatok: kocka élén áll ábrázolni Monge féle ábrázolással csúcsán álló , élén álló oktaéder ábrázolása monge féle ábrázolással teraéder lapján , csúcsán és élén áll szintén monge ábrázolással.
|
|
|
| [954] Hajba Károly | 2007-11-28 08:11:00 |
 Még mindig kevés az infó. A négyzet melyik egyenese az egyenes és melyik pontja a pont? Mikorra kellene? Péntekre tudnám elkészíteni a segédábrát, de majd az 'ábrázoló geometriában', oda való.
|
| Előzmény: [953] tyotyke, 2007-11-28 07:52:38 |
|
| [953] tyotyke | 2007-11-28 07:52:38 |
 Szia! Igen elhamarkodottan írtam le a dolgokat.Egy pont és egy egyenes két képéről van szó, és ebből kell egy kockát szerkesztenünk, csak a négyzetet azért irtam, mert az már 2-es és onnantól kezdve a magasságvonalak szerkesztésével a kocka csak néhány lépés. Fel kell vennünk egy első fővonalat......stb., leforgatotott háromszögből berajzoljuk a valódi kocka oldalhosszát.....Ezek lépések a szerkesztésből. Remélem igy már érthető!!!:) Köszönöm a segítséget,érdeklődést! Üdv!
|
|
| [952] HoA | 2007-11-27 18:47:11 |
 Szia! Biztos vagy te abban, hogy ez két egyenes és két pont a síkban? Nem egy ábrázoló feladatról van szó és egy pont és egy egyenes két vetületét látjuk? ( Ehhez javasolnám az "ábrázoló geometria" témakört ). És mi a feladat? Hogy kell egy (vagy két?) pontból és egyenesből négyzetet és kockát szerkeszteni? Az ábrázoló esetben el tudok képzelni olyan feladatot, hogy szerkesszünk négyzetet, melynek egyik csúcsa az adott pont, oldalegyenese/átlóegyenese az adott egyenes. Vagy szerkesszünk kockát, melynek egyik csúcsa az adott pont, egyik élének/lapátlójának/testátlójának egyenese az adott egyenes. Ezek egyike a feladat?
|
| Előzmény: [950] tyotyke, 2007-11-27 12:18:55 |
|
|
| [950] tyotyke | 2007-11-27 12:18:55 |
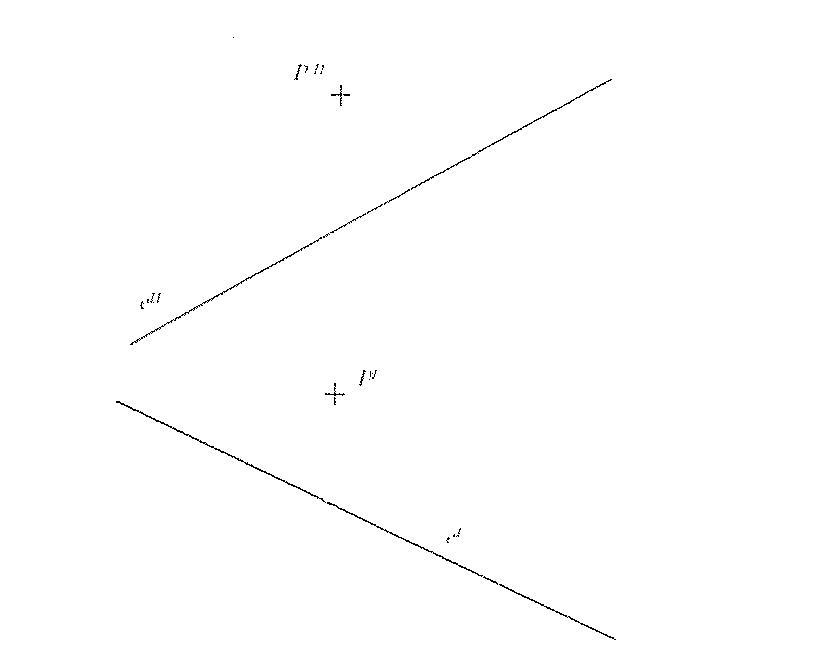
 Sziasztok! Végig néztem a forum hozzászólásokat és meg kell hogy állapítsam, hogy itt profik társalognak! Ebből adódóan jött az ötletem, hogy a Ti segítségeteket fogom kérni és remélem segítetek is nekünk! Egy zh feladat megoldására lennénk kiváncsiak, szerkesztővonalak ábrázolásával és némi magyarázattal.A feladat általában egy tetszőlegesen adott két egyenes és két pont a síkban, amiből először egy négyzetet, majd abból egy kockát kell szerkeszteni. Megpróbálom a kiinduló ábrát csatolni, remélem sikerül. Segítségeteket előre is köszönöm!
|
|
|
|
| [947] BohnerGéza | 2007-11-26 13:20:09 |
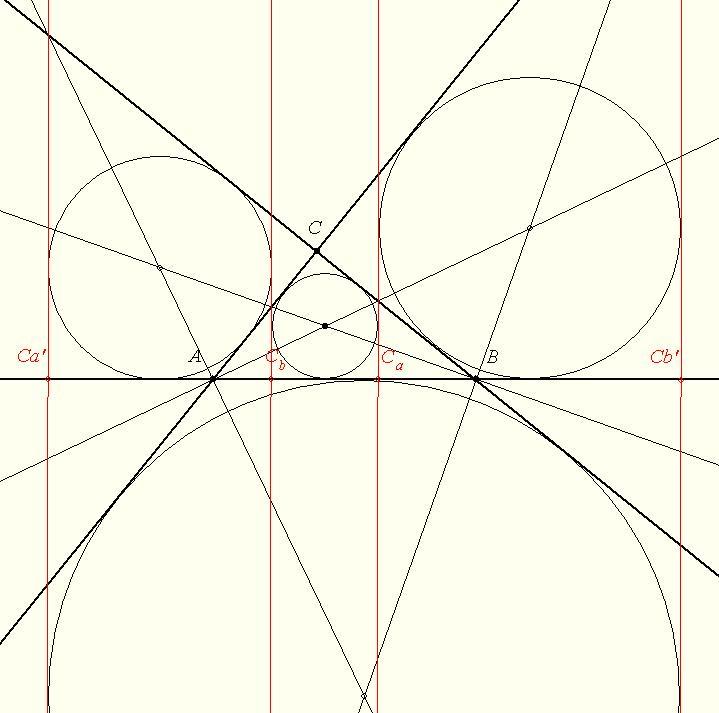
 A feladatot a következő érdekes észrevétel miatt tűztem ki:
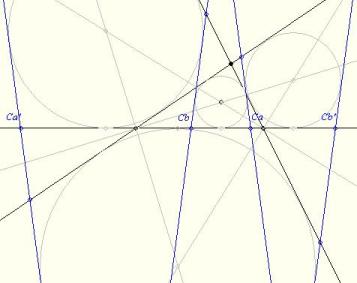
Legyen ABC C-nél derékszögű. Tükrözzünk a C-n nem átmenő szögfelezőkre! Például Ca' a C-nek az A-hoz tartozó külső szögfelezőre való tükörképe. Ekkor AC egyenes képe AB lesz és BC képe a Ca'-n átmenő AB-re merőleges egyenes, amely érint a b és c indexű hozzáírt köröket. ....
|
 |
| Előzmény: [946] HoA, 2007-11-26 10:29:32 |
|






 =2
=2 , mivel a E a DCB háromszögben a körülírható kör kp-a. De így CDE
, mivel a E a DCB háromszögben a körülírható kör kp-a. De így CDE
 stb.)
stb.) 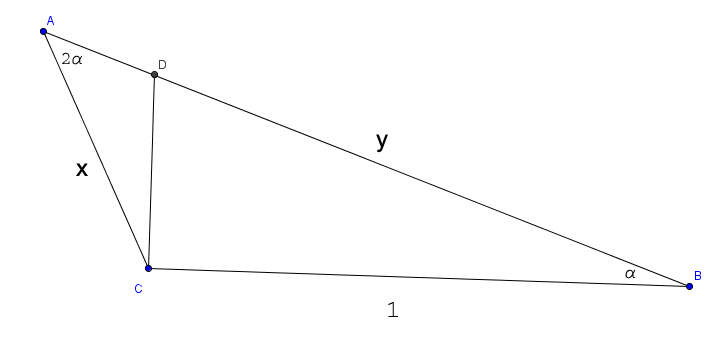

 C, vagy P
C, vagy P

 irányszögére - az MA = A'O iránytól mérve
irányszögére - az MA = A'O iránytól mérve  <
<