| [182] Antal János Benjamin | 2011-12-02 22:00:56 |
 Sziasztok!
Az i277-es feladatban, a program ahogy kirajzolta a képet, azonnal záródjon is be, vagy egy billentyűlenyomáskor záródjon be?
Köszi
|
|
|
| [180] Adrián Patrik | 2011-11-16 22:48:57 |
 S66-ban feltehetjük-e, hogy a házakat 0-tól N-1-ig számozzuk?
|
|
|
| [178] Róbert Gida | 2011-11-12 22:09:45 |
 OK, bár annak nem látom sok értelmét, hogy ismert feladatokat tűznek ki, mondjuk ez I jelű feladat volt, de S-ben is volt teljesen ismert probléma, mondjuk a sudoku.
A probléma spec. esete annak, amikor egész számok vannak a téglalapba írva, és keressük azt a téglalapot, amiben a számok összege a legnagyobb. Magasabb dimenzióban is láttam már kitűzve ezt a feladatot, nincs nagy újdonság benne, csak többet kell írni.
De d=2 dimenzióban is érdekes a feladat, nem ismert a bonyolultsága, nyilván n2 művelet kell, de O(n3)-nél van gyorsabb algoritmus is. Talán 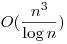 -es, nem emlékszem. -es, nem emlékszem.
Egy másik már érdekesebb általánosítás, amikor nem egy téglalapba, hanem egy tóruszra írjuk az egész számokat, és keressük a téglalapot amiben a számok összege a legnagyobb.
|
| Előzmény: [177] Adrián Patrik, 2011-11-11 20:44:51 |
|
|
| [176] Róbert Gida | 2011-11-11 15:48:33 |
 I274. Amit második megoldásnak írtok az egy O(n2*m2)-es algoritmus. De van O(n*m*min(n,m))-es megoldás is. Igazából halálismert.
A tiétek nem is hinném, hogy n=m=500 esetén lefutna egy perc alatt a gépeteken.
|
|
| [175] Róbert Gida | 2011-10-31 16:55:18 |
 Igen, így már helyes a kód.
Egyébként tree[i] méretére helyes volt az n>>i. Egy bizonyítás erre: 2-hatványok összeadása miatt látható, hogy pos=u*2i-1 valamilyen u égeszre, így pos2=w*2i-1 is teljesül, de akkor pos2>>i=w-1 és n>pos2=w*2i-1 miatt (n>>i) w, kettőt összerakva (pos2>>i)<(n>>i). Talán emiatt is célszerű pos=-1-ről indulni, hogy tree[i] mérete n>>i legyen. w, kettőt összerakva (pos2>>i)<(n>>i). Talán emiatt is célszerű pos=-1-ről indulni, hogy tree[i] mérete n>>i legyen.
|
| Előzmény: [174] Engedy Balázs, 2011-10-31 04:22:00 |
|
| [174] Engedy Balázs | 2011-10-31 04:22:00 |
 Ezt azért nem nevezném interval tree-nek. Amit írsz, az valójában teljesen analóg a versenyző által készített megoldással, annyi különbséggel, hogy te csak a bináris fa leveleiben "tárolsz" elemeket, illetve egy tömböt indexelsz ügyesen ahelyett, hogy külön objektumok lennének a csúcsok.
Mindenesetre ha már lekódoltad, kirakom ezt is megoldásnak, köszönjük! (Annyit módosítottam rajta, hogy a szükséges méretű tömböket foglalja le dinamikusan, ne pedig eggyel rövidebbet, mert így gyakran elszállt. Remélem, most már jó.)
|
| Előzmény: [173] Róbert Gida, 2011-10-30 23:35:47 |
|
|
| [172] Engedy Balázs | 2011-10-30 21:06:32 |
 Az S.64. javítása épp most készült el, már ki is került.
Egyébként ugyanaz a javítási határidő/időköz, mint a többi pontversenyben: igyekszünk a következő feladat határideje előttre kijavítani, de ez nem mindig sikerül.
|
| Előzmény: [171] H2CO3, 2011-10-29 18:05:57 |
|
| [171] H2CO3 | 2011-10-29 18:05:57 |
 Szaisztok! Csak annyit szeretnék kérdezni, hogy az informatika feladatokat milyen időközönként/határidővel javítják? Hamarosan az októberi forduló beküldési határideje is lejár, de még a szeptemberi feladatok sincsenek javítva... remélem, nem költözött el az e-munkafüzet...?
Köszi a válaszokat!
|
|
|
| [168] Adrián Patrik | 2011-10-23 19:02:38 |
 Az S.65. feladattal kapcsolatban szeretném megkérdezni, hogy a második és harmadik példában biztosan helyes-e a megadott kimenet.
|
|
| [167] Engedy Balázs | 2011-10-02 10:11:20 |
 A feladatban leírt feltételeket/korlátokat egyfajta szerződésként tekintsd: mi garantáljuk, hogy csak ennek eleget tevő -- helyes -- bemenetekkel hívjuk meg a megoldásod, te pedig (a maximális pontszámért) garantálod, hogy a helyes bemenetekre hiba nélkül lefut és helyes választ ad a programod. (Illegális bemenetre akár el is szállhat, itt ez nem érdekes.)
Tehát ellenőrzést semmiképpen ne végezz, viszont bizonyosodj meg alaposan, hogy minden (a feladat szövege által nem kizárt) speciális esetet lekezeltél.
|
| Előzmény: [166] Antal János Benjamin, 2011-10-01 00:02:15 |
|
| [166] Antal János Benjamin | 2011-10-01 00:02:15 |
 Új vagyok ebben a komalban, és nem tudom, hogy azt kell e vizsgalni, pl S64-nél hogy a tomb elemeinek szama nem-e kisebb a torlesek szamanal. Kell akármilyen hibaellenorzest csinalni a feladatokban?
|
|
|
| [164] Róbert Gida | 2011-07-31 18:11:03 |
 i270 pdf file érdekes, először azt hittem, hogy egy 80 évre titkosított kormánydokumentumot látok a sok fekete kitakart rész miatt. Ezt persze még gyakorolni kell, mert a kitakart email címre még rá lehet kattintani, sőt az url címre is.
Feltett s63.c kódnál fordítás nélkül találjuk meg, hogy hol kapnánk warningot -Wall-al fordítva.
|
|
|
| [162] Borsos Zalán | 2011-04-30 09:37:22 |
 S.62. Kérdés: A doboz átmérője illetve a labdák sugarai mindig egész számok?
|
|
|
| [160] Python | 2011-02-14 14:33:52 |
 Programnyelvnek Python a legjobb szerintem - talán az egyik legkönnyebben tanulható és használható programnyelv, de nagyobb dolgokat is lehet benne írni. A www.python.org oldalról ingyenesen letölthető, itt angolul elég sok leírást is lehet találni hozzá, de magyar fordításokat is lehet találni (google).
|
| Előzmény: [159] Blinki Bill, 2011-02-12 18:30:50 |
|
| [159] Blinki Bill | 2011-02-12 18:30:50 |
 Sziasztok!
Mi tanácsolnátok egy 7-es fiúnak,aki tök 0-ról akar egyedül programozással ismerkedni. Programnyelv, szakirodalom, ....?
Előre is kösz.
|
|
|
| [157] Róbert Gida | 2011-02-12 16:21:00 |
 Feltettem ide, némi megjegyzéssel együtt: http://ideone.com/aiMuI
További megjegyzések a kódhoz:
1. észrevétel: 2 ds (súlyozott) Manhattan távolság az az 1 ds (súlyozott) Manhattan távolságok összege. Így a feladat átjátszható 1 dimenzióra.
2. észrevétel: az eredeti x, illetve y koordináták között is felvétetik az optimum. Ezt könnyű belátni, mert 2 szomszédos rácspont között 1 dimenzióban a súlyozott Manhattan távolság lineárisan változik.
Volt benne némi különmunka, hogy kijöjjek a 3 for ciklussal és 1 if-fel. De sikerült.
|
| Előzmény: [154] turkish, 2011-02-12 08:15:07 |
|
